Archivo PDF, 1 slide por página, 155 KB

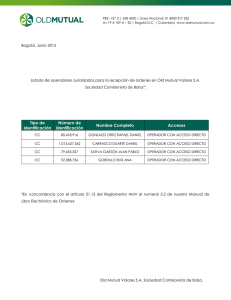
CONCEPTOS BÁSICOS DE
MECÁNICA CUÁNTICA
MECÁNICA CLÁSICA
El movimiento de una partícula esta gobernado por
la segunda Ley de Newton
d 2x
F = ma = m 2
dt
F: fuerza que actúa sobre la partícula
m: masa de la partícula
a: aceleración
t: tiempo
Dado el estado de un sistema en cualquier
instante de tiempo, su estado y movimientos
futuros quedan completamente determinados.
Conociendo en forma exacta el estado presente de
un sistema mecanoclásico, se puede predecir su
estado futuro.
1
MECÁNICA CUÁNTICA
Principio de incertidumbre de Heisenberg:
no es posible determinar simultáneamente la posición
y velocidad exactas de una partícula microscópica.
No es posible realizar una predicción completa del
estado futuro del sistema.
FUNCIÓN DE ONDA Y ECUACIÓN DE
SCHRÖDINGER
Ψ
FUNCIÓN DE ONDA
FUNCIÓN DE ESTADO
h ∂Ψ ( x, t )
h 2 ∂ 2 Ψ ( x, t )
+ V ( x, t )Ψ ( x, t )
=−
−
2
2m ∂x
i
∂t
ECUACIÓN DE SCHRÖDINGER DEPENDIENTE DEL TIEMPO
¿Qué representa Ψ?
Ψ ( x, t ) dx
Max Born
2
2
ECUACIÓN DE SCHRÖDINGER (ES)
INDEPENDIENTE DEL TIEMPO
Si V no depende de t
h ∂Ψ ( x, t )
h 2 ∂ 2 Ψ ( x, t )
−
=−
+ V ( x, t )Ψ (x, t )
2
i
∂t
2m ∂x
Separación de variables
Ψ ( x, t ) = f (t )ψ ( x )
Tomando derivadas parciales
∂Ψ (x, t ) df (t )
=
ψ (x )
∂t
dt
∂ 2 Ψ ( x, t )
d 2ψ (x )
= f (t )
∂x 2
dx 2
Sustituyendo
d 2ψ ( x )
h df (t )
h2
−
ψ (x ) = −
f (t )
+ V ( x ) f (t )ψ ( x )
i dt
dx 2
2m
Dividiendo entre f(t)ψ(x)
h 1 df (t )
h 2 1 d 2ψ ( x )
−
=−
+ V (x )
2
i f (t ) dt
2m ψ ( x ) dx
Ambos miembros son constantes!!!
3
Llamamos E a la constante de separación
−
h 1 df (t )
=E
i f (t ) dt
ln f (t ) = −
df (t )
iE
= − dt
f (t )
h
f (t ) = Ae
iE
t +C
h
f (t ) = e
− iEt
− iEt
h
h
h 2 1 d 2ψ ( x )
−
+ V (x ) = E
2m ψ ( x ) dx 2
h 2 d 2ψ ( x )
−
+ V ( x )ψ ( x ) = Eψ ( x )
2m dx 2
ECUACIÓN DE SCHRÖDINGER INDEPENDIENTE DEL TIEMPO
partícula de masa m que se mueve en una dirección
E: energía total del sistema
Ψ ( x, t ) = e − iEt hψ ( x )
4
Ψ es una función
significado físico.
experimentalmente
probabilidad
2
Ψ
[
compleja que no tiene
La cantidad observable
es
la
densidad
de
= Ψ *Ψ
]
Ψ ( x, t ) = e −iEt hψ ( x ) e −iEt hψ (x )
2
*
E es un numero real
Ψ ( x, t ) = eiEt hψ * ( x )e −iEt hψ ( x )
2
Ψ (x, t ) = ψ * ( x )ψ (x ) = ψ ( x )
2
2
La densidad de probabilidad no cambia con el
tiempo: ESTADOS ESTACIONARIOS
5
OPERADORES
Un operador es una instrucción o regla que
transforma una función en otra
∧
Ejemplo: D = ∂
Operador derivada
∂x
) (
)
∂ x 2 + 3e x
D x + 3e =
= 2 x + 3e x
∂x
∧
(
x
2
SUMA DE OPERADORES
⎛∧ ∧⎞
⎛∧⎞
⎛∧⎞
(
)
(
)
+
=
+
A
B
f
x
A
f
x
⎜
⎟
⎜ ⎟
⎜ B ⎟ f (x )
⎝
⎠
⎝ ⎠
⎝ ⎠
DIFERENCIA DE OPERADORES
⎛∧ ∧⎞
⎛∧⎞
⎛∧⎞
(
)
(
)
−
=
−
A
B
f
x
A
f
x
⎜
⎟
⎜ ⎟
⎜ B ⎟ f (x )
⎝
⎠
⎝ ⎠
⎝ ⎠
PRODUCTO DE OPERADORES
⎛∧ ∧⎞
⎜ A B ⎟ f (x ) =
⎝
⎠
∧ ∧
⎡
⎤
A⎢ B f ( x )⎥
⎣
⎦
Ejemplo
(
)
(
)
(
)
∧
⎡∧ 2
x ⎤
3 D x + 3e = 3⎢ D x + 3e ⎥ = 3 2 x + 3e x = 6 x + 9e x
⎣
⎦
∧ ∧
2
x
∧
6
∧ ∧
∧ ∧
∧ ∧
(
)
3 D f ( x ) = D 3 f ( x ) = D 3 x 2 + 3e x = 6 x + 9e x
En general no podemos esperar el mismo resultado
al conmutar los operadores
∧ ∧
d
d
D x f ( x ) = [xf ( x )] = f ( x ) + x
f (x )
dx
dx
⎛ ∧ ∧⎞
D x f ( x ) = ⎜1 + x D ⎟ f ( x )
⎠
⎝
∧ ∧
⎤
⎡d
x D f ( x ) = x ⎢ f ( x )⎥
⎦
⎣ dx
∧ ∧
∧
∧ ∧
∧ ∧
En general A B y B A son operadores diferentes
∧ ∧
⎡
⎤
CONMUTADOR ⎢ A, B ⎥
⎣
⎦
⎡∧ ∧⎤ ∧ ∧ ∧ ∧
⎢⎣ A, B ⎥⎦ = A B − B A
⎛ ∧ ∧⎞
D x f ( x ) = ⎜1 + x D ⎟ f ( x )
⎠
⎝
∧ ∧
∧ d
⎡
⎤
x D f ( x ) = x ⎢ f ( x )⎥
⎣ dx
⎦
∧ ∧
∧ ∧
∧ ∧
D x = 1+ x D
7
∧ ∧
∧ ∧
⎡ d ∧⎤ ⎡ ∧ ∧⎤
⎢⎣ dx , x ⎥⎦ = ⎢⎣ D, x ⎥⎦ = 1 + x D − x D = 1
No
conmutan
CUADRADO DE UN OPERADOR
∧2
∧ ∧
A = AA
OPERADOR LINEAL
∧
A es un operador lineal si y solo si cumple las dos
propiedades siguientes
∧
∧
∧
A[ f ( x ) + g ( x )] = A f ( x ) + A g ( x )
∧
∧
A[cf ( x )] = c A f ( x )
f y g funciones arbitrarias
c constante arbitraria
d
es lineal?
dx
d
[ f (x ) + g (x )] = df (x ) + dg (x ) = d f (x ) + d g (x )
dx
dx
dx
dx
dx
d
[cf (x )] = c d f (x )
dx
dx
d
dx
es lineal
8
FUNCIONES PROPIAS (eigenfunctions) Y
VALORES PROPIOS (eigenvalues)
∧
A f ( x ) = kf ( x )
f(x): función propia del operador
k: valor propio del operador
Ejemplo: e2x es función propia el operador d/dx
con valor propio 2
d 2x
e = 2e 2 x
dx
ECUACIÓN DE SCHRÖDINGER Y
OPERADOR HAMILTONIANO
h 2 d 2ψ ( x )
−
+ V ( x )ψ ( x ) = Eψ ( x )
2
2m dx
⎡ h2 d 2
⎤
+ V ( x )⎥ψ ( x ) = Eψ ( x )
⎢−
2
m
dx
2
⎣
⎦
∧
OPERADOR HAMILTONIANO
H
9
∧
H ψ ( x ) = Eψ ( x )
ECUACIÓN DE
SCHRÖDINGER
La ES es una ecuación de valores propios de un
operador que tiene la siguiente forma
∧
h2 d 2
H =−
+ V (x )
2
2m dx
OPERADOR
HAMILTONIANO
El valor propio del Hamiltoniano es la energía
total del sistema!!!
∧
V = V (x )
OPERADOR ENERGIA POTENCIAL
Clásicamente la energía cinética viene dada por
p 2 mv 2
K=
=
2m
2
Si suponemos que los operadores que representan a
la energía y al momento en la mecánica cuántica
guardan la misma relación que las magnitudes
equivalentes en mecánica clásica
10
2
⎡ h2 d 2 ⎤
2 d
= −h
p x = 2m K = 2m ⎢ −
2⎥
2
m
dx
dx 2
⎣
⎦
∧2
∧
∧
p x = −ih
d h d
=
dx i dx
OPERADOR
MOMENTO LINEAL
Es un postulado general de la
mecánica cuántica que a cada
propiedad física le corresponde un
operador mecanocuántico
Como relacionamos los operadores mecanocuánticos
con las propiedades correspondientes del sistema?
∧
B operador correspondiente a la propiedad física B
∧
B fi = bifi
i=1,2,3,.......
Una medida de la propiedad B debe dar uno de los
∧
valores propios bi del operador B
Los únicos valores propios que
pueden obtenerse para la energía del
sistema son los valores propios del
operador Hamiltoniano!
11
ES TRIDIMENSIONAL PARA UN SISTEMA
DE VARIAS PARTICULAS
h2 ⎛ ∂2
∂2
∂2 ⎞
⎜
⎟ + V ( x, y , z )
H =−
+
+
2m ⎜⎝ ∂x 2 ∂y 2 ∂z 2 ⎟⎠
∧
⎛ ∂2
∂2
∂2 ⎞
∇ = ⎜⎜ 2 + 2 + 2 ⎟⎟
∂y
∂z ⎠
⎝ ∂x
2
OPERADOR
LAPLACIANO
La ES independiente del tiempo para una partícula
en tres dimensiones es entonces
⎡ h2 2
⎤
∇ + V ( x, y, z )⎥ψ ( x, y, z ) = Eψ (x, y, z )
⎢−
2
m
⎣
⎦
Consideremos un sistema tridimensional de n
partículas. Sea la partícula i que tiene masa mi y
coordenadas (xi,yi,zi) donde i=1,2....n
12
La energía cinética es la suma de las energías cinéticas
de las partículas individuales
T=
(
)
(
)
(
2
2
2
2
2
p x21 + p y21 + p z21 +
p x22 + p y22 + p z22 + ... +
p xn
+ p yn
+ p zn2
2m1
2m2
2mn
)
El operador energía cinética es
h2 ⎛ ∂2
h2
∂2
∂2 ⎞
⎜⎜ 2 + 2 + 2 ⎟⎟ − ... −
T =−
2m1 ⎝ ∂x1 ∂y1 ∂z1 ⎠
2mn
∧
∧
⎛ ∂2
∂2
∂2 ⎞
⎜⎜ 2 + 2 + 2 ⎟⎟
⎝ ∂xn ∂yn ∂z n ⎠
h2 2
T = −∑
∇i
i =1 2mi
n
⎛ ∂2
∂2
∂2 ⎞
∇ = ⎜⎜ 2 + 2 + 2 ⎟⎟
∂yi
∂zi ⎠
⎝ ∂xi
2
i
Normalmente nos limitamos a los casos donde la
energía potencial depende solo de las 3n
coordenadas
V = V ( x1 , y1 , z1 ,..., xn , yn , z n )
13
El operador Hamiltoniano para un sistema de n
partículas en tres dimensiones es entonces:
∧
h2 2
H = −∑
∇ i + V ( x1 ,..., z n )
i =1 2 mi
n
y la ecuación de Schrödinger independiente del
tiempo es
⎡ n h2 2
⎤
(
)
−
∇
+
V
x
,...,
z
i
1
n ⎥ψ = Eψ
⎢ ∑
2
m
i
⎣ i =1
⎦
donde la función de onda independiente del
tiempo es una función de las 3n coordenadas de las
partículas
ψ = ψ ( x1 , y1 , z1 ,..., xn , yn , z n )
14
TEOREMAS DE LA MECANICA CUANTICA
NOTACION BRACKET
∫f
*
m
∧
∧
∧
A f n dτ = f m A f n = m A n
fm y fn dos funciones
Se asume que se toma la conjugada compleja de la
función que aparece en primer lugar
∫f
∫f
*
m
∧
A f n dτ
∧
Elemento de matriz del operador A
f dτ = f m f n = m n
*
m n
[∫ f
]
*
f dτ = ∫ f n* f m dτ
*
m n
fm fn
y como
entonces
*
= fn fm
15
OPERADORES HERMÍTICOS
∧
A operador lineal que representa la propiedad física A
El valor medio de A es
∧
A = ∫ψ Aψdτ
*
El valor medio de una magnitud física debe ser real
A = A* = A
*
⎛
⎞
*
=
ψ
A
ψ
d
τ
ψ
A
ψ
∫
∫ ⎜ ⎟ dτ
∧
∧
⎝
⎠
Un operador lineal que satisface esta condición se
denomina hermítico
En general, un operador hermítico es un operador
lineal que satisface
∫f
*
m
∧
A f n dτ = ∫
*
⎛ ∧ ⎞
f n ⎜ Af m ⎟ dτ
⎝
⎠
∧
∧
*
fm A fn = fn A fm
16
¿El operador energía potencial es hermítico?
∫
∞
f n (x )[V ( x ) f m (x )] dx = ∫
*
−∞
∞
−∞
∞
f n ( x )V * f m* ( x )dx = ∫ f m* ( x )V * f n ( x )dx
−∞
V es hermítico
El operador energía cinética también es hermítico
Se puede demostrar que la suma de dos operadores
hermíticos es un operador hermítico
∧
∧
∧
H = T +V
TEOREMA 1
∧
Los valores propios de un
operador
hermítico
son
números reales
hermítico, entonces satisface
A
∫f
Operador Hamiltoniano es
hermítico
*
m
∧
A f n dτ = ∫
*
⎛ ∧ ⎞
f n ⎜ Af m ⎟ dτ
⎝
⎠
queremos demostrar que ai=ai*
17
ai valores propios
∧
A g i = ai g i
gi funciones propias
fm=fn=gi
*
⎛ ∧ ⎞
∫ gi A gi dτ = ∫ gi ⎜⎝ Agi ⎟⎠ dτ
*
∫g
*
i
∧
∧
*
⎛ ∧ ⎞
* *
g
∫ i ⎜⎝ Agi ⎟⎠ dτ = ∫ gi ai gi dτ
A g i dτ = ∫ g i ai g i dτ
*
ai ∫ g i g i dτ = ai
*
*
(a − a )∫ g
∫ g i g i dτ
*
*
(a − a )∫ g
i
2
*
i
i
i
i
*
i
g i dτ = 0
dτ = 0
(a − a ) = 0
*
i
i
Los valores propios de un operador hermítico
son reales
18
TEOREMA 2
Dos funciones propias∧ de un
operador hermítico
B que
corresponden a valores propios
diferentes son ortogonales
Dos funciones f1 y f2 dependientes del mismo
conjunto de coordenadas son ortogonales si
∫
f1* f 2 dτ = 0
∧
Suponiendo que
∧
B F = sF
B G = tG
F y G dos funciones propias del operador
queremos demostrar
*
F
∫ Gdτ = F G = 0
Condición de hermiticidad
∧
F BG = F tG
F tG = G sF
*
∧
*
∧
F BG = G B F
∧
G BF
*
= G sF
*
t F G = s* G F
*
19
s=s
F G = G F
*
t F G =s G F
Como s≠t
*
*
(t − s ) F
=s F G
G =0
F G =0
Dos funciones propias de un operador hermítico
que corresponden a valores propios diferentes
son ortogonales
Elegimos funciones propias ortogonales
*
g
∫ i g j dτ = 0
Si i≠j
Elegimos funciones propias normalizadas
*
g
∫ i gi dτ = 1
Elegimos funciones propias ortonormales
*
g
∫ i g j dτ = gi g j = δ ij
δij =1
i=j
δij =0
i≠j
δij = delta de Kronecker
20
POSTULADOS DE LA MECÁNICA
CUÁNTICA
POSTULADO 1
El estado de un sistema cuántico esta descrito
por una función Ψ de las coordenadas y del
tiempo. Esta función llamada función de
estado o función de onda, contiene toda la
información que es posible conocer acerca del
sistema. Postulamos además que la función Ψ
es monoevaluada, continua y cuadráticamente
integrable.
POSTULADO 2
A cada observable físico de la mecánica
clásica le corresponde un operador hermítico
lineal
21
POSTULADO 3
En cualquier medida del observable asociado al
∧
operador lineal A , los únicos valores que serán
observables serán los valores propios an que
satisfacen la ecuación
∧
A φ n = anφ n
donde φn son las funciones propias asociadas a cada
estado del sistema (funciones de onda bien
comportadas)
POSTULADO 4
∧
Si A es cualquier operador hermítico lineal que
representa a un observable
físico, entonces las
∧
funciones propias φn de A forman un conjunto
completo.
Este postulado nos permite desarrollar la función de
onda de cualquier estado como una superposición
de las funciones propias ortonormales de cualquier
operador mecanocuántico
ψ = ∑ ciφi
i
22
POSTULADO 5
Si un sistema ocupa un estado descrito por una
función de onda normalizada ψ(n), entonces, el
valor medio del observable asociado al
∧
operador A estará dado por
∧
a = ∫ψ (r ) Aψ (r )dr
*
donde la integración se realiza en todo el espacio
accesible al sistema
∧
Aψ n (r ) = anψ n (r )
si
El valor medio del observable estará dado por
∧
a = ∫ψ n (r ) Aψ n (r )dr = ∫ψ n (r )anψ n (r )dr = an ∫ψ n (r )ψ n (r )dr
*
∫ψ (r )ψ (r )dr = 1
*
n
n
*
*
a = an
Si un sistema ocupa un estado que es una función
propia de un operador, cuando midamos el
observable asociado a ese operador, obtendremos
como resultado el valor propio del operador.
23
POSTULADO 6
La evolución temporal del estado de un sistema
mecanocuaántico no perturbado viene dado por
la ecuación de Schrödinger dependiente del
tiempo
h ∂Ψ ( x, t )
h 2 ∂ 2 Ψ ( x, t )
−
=−
+ V ( x, t )Ψ ( x, t )
2
2m ∂x
∂t
i
EL HAMILTONIANO MOLECULAR
El Hamiltoniano para un sistema de n partículas
∧
h2 2
H = −∑
∇ i + V ( x1 ,..., z n )
i =1 2mi
n
El Hamiltoniano molecular
∧
h2
H =−
2
1 2 h2
∇α −
∑
2me
α mα
∧
∧
∧
H = T +V
zα z β
z
1 2
1
∇
+
− ∑∑ α + ∑∑
∑i m i ∑
∑
α
i riα
i i > j rij
α β >α rαβ
i
α y β denotan a los núcleos
i y j denotan a los electrones
24
Las funciones de onda y las energías de una molécula
se obtienen a partir de la ES
∧
H ψ (qi , qα ) = Eψ (qi , qα )
APROXIMACIÓN DE BORN-OPPENHEIMER
Los núcleos son mucho más pesados que los electrones.
Es posible desacoplar ambos movimientos.
ψ (qi , qα ) = ψ el (qi ; qα )ψ nuc (qα )
La función de onda electrónica depende
paramétricamente de la posición de los núcleos
APROXIMACIÓN DE LOS NÚCLEOS FIJOS
Es posible hacer nula la componente de energía
cinética de los núcleos.
Ecuación
para
el
movimiento electrónico
⎞
⎛ ∧
⎜ H el + VNN ⎟ψ el = Uψ el
⎠
⎝
∧
H el
Hamiltoniano puramente electrónico
∧
h2
H el = −
2me
1
z
1
α
+ ∑∑
∑ m ∇ − ∑∑
r
r
α
i
i
2
i
i
iα
i
i> j
ij
25
⎛ ∧
⎞
⎜ H el + VNN ⎟
⎝
⎠
zα z β
β >α rαβ
VNN = ∑ ∑
α
hamiltoniano electrónico incluyendo la
repulsión internuclear
repulsión internuclear
U energía electrónica incluyendo la repulsión nuclear
Omitiendo VNN
∧
H el ψ el = Eelψ el
Eel energía puramente electrónica
U = Eel + VNN
SUPERFICIES DE ENERGÍA POTENCIAL
La energía electrónica del sistema, obtenida mediante
la solución de la ES electrónica es una función de las
coordenadas nucleares y determina la superficie de
energía potencial (PES)
Hay una serie de temas fundamentales relacionados
con las PES que tienen mucha importancia en
química
•Localización de puntos estacionarios
•Determinación de caminos de reacción
•Cálculo de trayectorias
26
LOCALIZACIÓN DE PUNTOS ESTACIONARIOS
• vector gradiente
• matriz Hessiana
Gradiente =0
PUNTO ESTACIONARIO
• estructuras de equilibrio
• estructuras de transición
(puntos de ensilladura)
Valores propios de
la matriz Hessiana
• todos positivos: mínimo. Todas las
frecuencias vibracionales reales.
• algunos positivos y algunos negativos:
punto de ensilladura. El orden del punto
de ensilladura está dado por el número de
valores propios negativos de la Hessiana.
Los puntos de ensilladura de primer orden
en general se asocian a las estructuras de
transición
27