x(m) t(s)

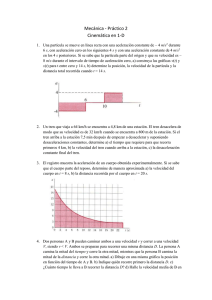
LICENCIATURA
EN QUÍMICAS
1.
FÍSICA
2002-2003
Un móvil se mueve en una trayectoria rectilínea.
La gráfica muestra la posición del móvil en
función del tiempo. Determínese la dirección y el
sentido de la velocidad y de la aceleración en los
distintos intervalos.
TEMA 2: CINEMÁTICA DE LA
PARTÍCULA
x(m)
t(s)
2.
Dos coches A y B están viajando en la misma dirección y sentido con velocidades vA y vB,
respectivamente. Cuando el A está a una distancia d detrás del B, el coche A comienza a frenar
siendo su aceleración a. Demuéstrese que para que ambos autos colisionen es necesario que se
verifique vA − vB > 2ad .
3.
Se dispara un proyectil con una velocidad inicial vo=40m/s formando un ángulo de 30º respecto a un
terreno horizontal. Determínese: i) el tiempo que tarda en caer a tierra; ii) alcance del proyectil; iii)
ángulo que forma con el terreno la dirección del proyectil en el instante en el que alcanza el suelo.
(Despréciese el rozamiento con el aire). (Resp: i) tvuelo ≈ 4 ⋅ s ; ii) xmax = 138.5 m; iii) ϕ=30º)
4.
Un tirador apunta a un blanco que está a una altura h. En el momento en el que el tirador dispara, el
blanco se deja caer. Demuéstrese que independientemente del módulo de la velocidad inicial de la
bala, ésta acertará al blanco.(Despréciese el rozamiento con el aire)
5.
Se lanza verticalmente un objeto hacia arriba de tal forma que tiene una velocidad de 19.6 m/s al
llegar a la mitad de la altura máxima. Calcúlese i) la altura máxima; ii) el módulo de la velocidad un
segundo después de haber sido lanzado; iii) el módulo de la aceleración al alcanzar la altura máxima.
(Despréciese el rozamiento con el aire). (Resp: i) hmax = 39.2 m; ii) v (t = 1s) = 17.9 m/s; iii)
a = 9.8 m/s2)
6.
Una partícula se está moviendo a lo largo de una parábola y=
instante la componente x de la velocidad es 3 m/s. Calcúlense
de la partícula en la posición x =2/3 m. (Resp: v = 3 i + 4j m/s y
7.
Una partícula que parte del reposo en t=0 se mueve según una trayectoria recta con una aceleración
a=aoe(-kt), siendo ao y k constantes positivas. Determínense las expresiones de la velocidad máxima
que puede adquirir la partícula y el espacio recorrido al cabo de un intervalo de tiempo t. (Resp:
a
a
a
vmax = o ; x(t) − x o = − o t + 2o (e −kt − 1) , el espacio recorrido d = x(t) − x o )
k
k
k
8.
Se hace girar una piedra que está en el extremo de una cuerda en un círculo vertical de radio 1.2m
con una velocidad de módulo constante de 1.5 m/s. El centro de la cuerda está a 1.5m del suelo.
¿Dónde caerá piedra si la soltamos cuando la inclinación de la cuerda es de 30º respecto a la
horizontal en el: i) 1er cuadrante; ii) 2do cuadrante; iii) aceleración de la piedra justo antes y justo
después de ser soltada en el caso i). (Resp: El plano del movimiento es el XY. Si el origen del sistema
de referencia es (0,0) y el centro de la circunferencia está en (0,1.5m); i) cae en x=0.44 m; ii) x= -
(1 m-1) x2 de modo que en cualquier
los vectores velocidad y aceleración
a = 18j m/s2.)
v2 1.44 m; iii) justo antes: a(t) = −
ur = −1.87ur (m/s2) ;justo después: a = −9.8j m/s2 )
R
9.
Un coche parte del reposo y en una vía circular de 400 m de radio va moviéndose con una
aceleración angular constante, de forma que a los 50 s el módulo de la velocidad alcanzada es de 72
km/h, para posteriormente mantener constante dicha valor. Calcúlese i) la aceleración tangencial en
1
LICENCIATURA
EN QUÍMICAS
FÍSICA
2002-2003
TEMA 2: CINEMÁTICA DE LA
PARTÍCULA
la primera etapa del movimiento; ii) la aceleración normal, total y la longitud de vía recorrida al cabo
de los 50 s. (Resp: i) at = 0.4 ut = 0.4uϕ m/s2 (suponiendo sentido antihorario); ii)
aN = 1 uN = −1ur m/s2; a = 1.16 = 1.07 m/s2, l=500 m).
10. Un chico se desliza por un tejado que forma un ángulo de 37º con la horizontal. Parte del reposo
desde el borde superior y llega al borde inferior del tejado, que tiene 8m de longitud y está a una
altura de 6 m sobre el suelo, con una aceleración de 5m/s2. Determinar i) las componentes de la
velocidad del chico al caer en la nieve; ii) tiempo total de su movimiento; iii) distancia entre la casa
y el punto en el que cae en la nieve. ( Resp: i) v = 7.14 i − 12.24 j m/s; ii) t=2.5s; iii) cae a una
distancia de 4.8 m de la casa).
11. Un comprador, que está en una tienda, puede recorrer una escalera mecánica en 30 s. Si la escalera
funciona y el comprador no camina sobre ella puede llevar al comprador al siguiente piso en 20 s.
¿Cuánto tiempo tardaría el comprador en subir por la escalera con ésta en marcha? (Resp.:12 s).
12. Un globo asciende con una rapidez de 12 m/s hasta una altura de 80 m sobre el suelo y entonces
deja caer un paquete. ¿Cuánto tarda en llegar el paquete al suelo?. (Despréciese el rozamiento con
el aire). (Resp: 5.4s).
13. Un avión de reacción vuela con una rapidez respecto al aire de 560km/h entre la ciudad A y la
ciudad B, que está situada a 600 km al este de A. Determínese el tiempo total de vuelo desde A
hasta B suponiendo que hay viento del oeste con una v=60 km/h constante. Calcúlese el tiempo de
vuelo para el viaje de retorno en las mismas condiciones. (Resp: i) 58min; ii) 72 min).
14. El vector de posición de una partícula referido a unos ejes tomados en el borde de una mesa es
r´= 3t2 i + 2t2 j m. La mesa se mueve con una aceleración constante de 1 m/s2 paralela al borde
tomado como eje O´X´. Hallar el vector de posición y la velocidad de la partícula con relación a unos
ejes fijos en la habitación y paralelos a los bordes de la mesa, sabiendo que O´ está en el punto
7 t2 (2,3) con respecto a los ejes fijos al iniciarse el movimiento. (Resp: rA = (2 +
) i + (2t2 + 3) j (m);
2
v A = 7 t i + 4tj (m/s):
15. Un tren viaja hacia el sur con una velocidad de 88 m/s bajo una lluvia desviada hacia el sur por el
viento. La trayectoria de las gotas forma un ángulo de 20º con la vertical con respecto a un
observador en tierra. Sin embargo, un pasajero del tren ve las trazas de la lluvia en la ventana
verticales. Determínese la velocidad de las gotas respecto al suelo. (Resp:
v = 88i − 242 j (m/s),
siendo OX la dirección de movimiento del tren).
16. Un río tiene una anchura de 100 m. Un nadador quiere cruzarlo a nado en dirección perpendicular a
la corriente y va a parar 20 m agua abajo. Si la velocidad del nadador es 2m/s, calcúlese la
velocidad del agua y el tiempo que tarda el nadador en cruzar el río. (Resp: i) v = 0.4 i m/s, siendo
OX la dirección de la corriente ; ii) t=50 s).
17. Un tren se mueve a 72 km/h cuando una linterna que está colgada al final del vagón y a una altura de
4.9 m respecto al suelo del vagón se suelta. Calcúlese la distancia recorrida por el tren hasta que la
lámpara cae al suelo. ¿Dónde cae con respecto al tren y a los rieles?. Deducir la trayectoria relativa
al tren y a los rieles.(Resp: i) 20m; ii) respecto al señor que está fuera del tren cae a 20 m de donde
empezó a caer, respecto a un señor en el tren cae en el mismo punto que el inicial).
2