Segunda convocatoria del curso 2012/2013

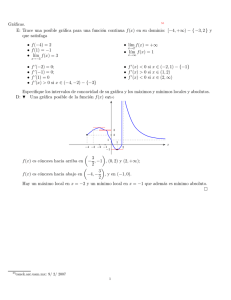
Cálculo I
Curso 2012/2013
21 de junio de 2013
Universidade de Vigo
Departamento de Matemática Aplicada II
E.T.S.I. Minas
(4 p.) 1) Se considera la función f (x) = x4 e1−x − 2.
a) Calcular los intervalos de crecimiento y decrecimiento de f y sus máximos
y mı́nimos relativos.
b) Calcular los puntos de inflexión de la gráfica de f y determinar los intervalos
de concavidad y convexidad.
c) Calcular las ası́ntotas horizontales y representar de forma aproximada la
gráfica de f .
d ) Hallar el polinomio de Taylor de grado 2 de f centrado en x0 = 1.
e) Probar que f tiene una única raı́z en el intervalo (0, 2) y acotarla en un
intervalo de longitud uno.
(3 p.) 2) Se considera el campo escalar en R2 dado por g(x, y) = 4xey − 4x2 − e2y − y 2 .
a) Determinar los puntos crı́ticos de g y estudiar si son máximos locales, mı́nimos locales o puntos de silla.
b) Calcular un vector unitario ~u ∈ R2 tal que la derivada direccional de g en
(0, 0) en la dirección de ~u sea cero.
(3 p.) 3) Se considera la superficie z = z(x, y) definida implı́citamente por la ecuación
3x2 z − x2 y 2 + 2z 3 − 3yz = 15.
a) Probar que z(1, 1) = 2.
b) Calcular la dirección de crecimiento más rápido de la función z(x, y) a partir
del punto (x0 , y0 ) = (1, 1).
c) Hallar la pendiente de la recta tangente a la curva de nivel z(x, y) = 2 en el
punto (1, 1).
SOLUCIONES
PROBLEMA 1.
(a) La función f es continua y derivable en R. Utilizando la fórmula de la derivada de
un producto y simplificando, se obtiene que la derivada de f es
f 0 (x) = x3 (4 − x)e1−x , ∀ x ∈ R.
Por tanto, f 0 (x) = 0 si y sólo si x = 0 o x = 4. Además f 0 (x) < 0 si x < 0 o x > 4
y f 0 (x) > 0 si 0 < x < 4. En consecuencia, f es estrictamente creciente en (0, 4) y
estrictamente decreciente en (−∞, 0) ∪ (4, ∞).
De los intervalos de crecimiento y decrecimiento se deduce que f alcanza en x = 0
un mı́nimo relativo y en x = 4 un máximo relativo.
(b) Aplicando de nuevo la fórmula de la derivada del producto a f 0 y simplificando, se
obtiene la derivada segunda de f :
f 00 (x) = x2 (x2 − 8x + 12)e1−x , ∀ x ∈ R.
Ası́,
f 00 (x) = 0 ⇐⇒
2
x =0
x2 − 8x + 12 = 0


 x=0 
x=2
⇐⇒


x=6
Analizando el signo de f 00 se obtiene que f 00 (x) > 0 si x < 2 o x > 6 y f 00 (x) < 0 si
2 < x < 6. Los puntos de inflexión de f son x = 2 y x = 6. La gráfica de f es convexa
en (−∞, 2) ∪ (6, ∞) y cóncava en (2, 6).
(c) Para determinar las posibles ası́ntotas horizontales, calculamos los lı́mites de f en
±∞.
Por una parte,
lı́m f (x) = lı́m x4 e1−x − 2 = ∞.
x→−∞
x→−∞
Por otra parte, usando la regla de L’Hôpital varias veces, se tiene:
4x3
x4
=
−2
+
lı́m
=
x→∞ ex−1
x→∞ ex−1
lı́m f (x) = lı́m x4 e1−x − 2 = −2 + lı́m
x→∞
x→∞
12x2
24x
24
= −2 + lı́m x−1 = −2 + lı́m x−1 = −2.
x−1
x→∞ e
x→∞ e
x→∞ e
= −2 + lı́m
En consecuencia, la recta y = −2 es una ası́ntota horizontal a la gráfica de f en
+∞.
Teniendo en cuenta los intervalos de crecimiento, la concavidad y la ası́ntota, obtenemos la siguiente forma aproximada de la gráfica de f :
2
0
2
6
4
-2
(d) De las expresiones de f y sus derivadas se obtiene:
f (1) = −1 ;
f 0 (1) = 3 ;
f 00 (1) = 5 .
Por tanto el polinomio de Taylor de grado 2 de f centrado en x0 = 1 es
p2 (x) = f (1) + f 0 (1)(x − 1) +
5
f 00 (1)
(x − 1)2 = −1 + 3(x − 1) + (x − 1)2 .
2
2
(e) En primer lugar, ya sabemos por el apartado a) que f 0 (x) 6= 0 , ∀ x ∈ (0, 2). Una
consecuencia del teorema de Rolle permite deducir que f no puede tener más de una
raı́z en el intervalo (0, 2).
Para probar que existe una raı́z, usamos el teorema de Bolzano:
f (0) = −2 < 0
f (2) =
16
− 2 > 0, ya que 16 > 2e.
e
Para acotar la raı́z en un intervalo de longitud uno, observemos que f (1) = −1 < 0.
Como el cambio de signo se produce en el intervalo (1, 2), la raı́z debe pertenecer a
dicho intervalo.
PROBLEMA 2.
(a) Los puntos crı́ticos de g son los puntos donde se anula el gradiente.
∂g
∂g
∇g(x, y) =
(x, y), (x, y) = 4ey − 8x , 4xey − 2e2y − 2y .
∂x
∂y
3
Igualamos a cero las dos derivadas parciales:

∂g


(x, y) = 0 ⇐⇒ 4ey = 8x ⇐⇒ ey = 2x

∂x
∂g



(x, y) = 0 ⇐⇒ 4xey − 2e2y = 2y
∂y
Sustituyendo ey = 2x en la parte izquierda de la segunda ecuación, se obtiene que
2y = 4xey − 2e2y = 8x2 − 8x2 = 0 =⇒ y = 0
Como x = ey /2 = 1/2, el único punto crı́tico es P = (1/2, 0).
La matriz hessiana es:

∂ 2g
 ∂x2
Hg(x, y) = 
 ∂ 2g
∂y∂x

∂ 2g
∂x∂y 
=
∂ 2g 
∂y 2
4ey
−8
4ey 4xey − 4e2y − 2
!
.
Para P = (1/2, 0), se tiene:
Hg(1/2, 0) =
−8
4
4 −4
.
Los menores principales de Hg(1/2, 0) son ∆1 = −8 < 0, ∆2 = 16 > 0. Por tanto,
Hg(1/2, 0) es definida negativa y g alcanza en P un máximo local.
(b) Si denotamos ~u = (u1 , u2 ) el vector buscado, la derivada direccional de g en (0, 0)
en la dirección de ~u es
u1
D~u g(0, 0) = ∇g(0, 0) · (u1 , u2 ) = (4, −2)
= 4u1 − 2u2 .
u2
Igualando a cero, se obtiene 4u1 = 2u2 y por tanto
~u = (u1 , 2u1 ) = u1 (1, 2).
En consecuencia, ~u es un vector unitario en la dirección de (1, 2) y podemos tomar
~u =
√
√ (1, 2)
= 1/ 5 , 2/ 5
k(1, 2)k
o ~u =
4
√
√ −(1, 2)
= −1/ 5 , −2/ 5 .
k(1, 2)k
PROBLEMA 3.
(a) Para x = y = 1, la expresión 3x2 z − x2 y 2 + 2z 3 − 3yz = 15 se convierte en
2z 3 − 1 = 15 y por tanto
√
3
2z 3 − 1 = 15 ⇐⇒ z 3 = 8 ⇐⇒ z = 8 = 2.
(b) La dirección de crecimiento más rápido es la del gradiente de z en el punto (1, 1):
∂z
∂z
∇z(1, 1) =
(1, 1), (1, 1) .
∂x
∂y
La función z = z(x, y) está definida implı́citamente por la expresión
F (x, y, z) = 3x2 z − x2 y 2 + 2z 3 − 3yz − 15 = 0.
Usando la regla de la cadena, tenemos:
∂F
∂F ∂z
∂z
−∂F/∂x
+
= 0 =⇒
=
∂x
∂z ∂x
∂x
∂F/∂z
∂F
∂F ∂z
∂z
−∂F/∂y
+
= 0 =⇒
=
.
∂y
∂z ∂y
∂y
∂F/∂z
Las derivadas parciales de F son
∂F
= 6xz − 2xy 2
∂x
;
∂F
= −2x2 y − 3z
∂y
;
∂F
= 3x2 − 3y + 6z 2 .
∂z
Por tanto,
∂z
−∂F/∂x
−6xz + 2xy 2
=
= 2
∂x
∂F/∂z
3x − 3y + 6z 2
∂z
−∂F/∂y
2x2 y + 3z
=
= 2
.
∂y
∂F/∂z
3x − 3y + 6z 2
;
Para x = 1, y = 1, z = 2, se tiene:
−10
−5
∂z
(1, 1, 2) =
=
∂x
24
12
;
∂z
8
1
(1, 1, 2) =
= .
∂y
24
3
Ası́, la dirección de crecimiento más rápido de la función z(x, y) a partir del punto
(1, 1) es
∇z(1, 1) = (−5/12 , 1/3) .
(c) La recta tangente a la curva de nivel en el punto (1, 1) es ortogonal al gradiente de
z en ese punto, que calculamos en el apartado anterior:
∇z(1, 1) = (−5/12 , 1/3) =
1
(−5, 4).
12
La ecuación de la recta tangente es
5
1
−5
(x − 1, y − 1)
= 0 ⇐⇒ −5x + 4y + 1 = 0 ⇐⇒ y = x − .
4
4
4
Finalmente, la pendiente de la recta es m = 5/4.
5