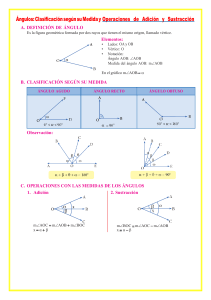
5 8 : / 9 x f R R f x / 2 9 g R R g x x

Matemática Discreta usando el computador 2012 (Matemática I)
Examen de Matemática I
27 de setiembre del 2012
Comentarios:
1. No podrán utilizarse funciones auxiliares, salvo que se indique explícitamente lo contrario, en cuyo caso
deberán definirse las mismas.
2. Las funciones predefinidas de Haskell podrán usarse solamente si se indica explícitamente.
Ejercicio 1 Sean f: AoB, g: A o(AoB), h: (AoA)oAoA, j: AoA, p:(AoB) o$, x: A , y: B
Indicar si las siguientes expresiones tienen tipo, en caso afirmativo indicarlo, justificando en
todos los casos su respuesta.
a) g x
b) g x x
c) g x (f x)
d) g x f
e) p f
f) p (g x) g) h j x h) h (j x) x
Ejercicio 2
Considerar la definición inductiva de naturales vista en el curso.
a) Definir la función producto: N ĺ N ĺ N que dados dos naturales a y b devuelve el producto de
ambos. (No se pueden usar la multiplicación)
b) Dar la secuencia de cómputo para (producto 5 3).
Ejercicio 3
Definir la función mezclar que dadas dos listas de enteros ordenadas en forma creciente,
devuelva la lista ordenada tambien en forma creciente, resultado de mezclar los elementos de
las dos listas. No se deberán utilizar funciones auxiliares.
Ejemplo:
mezclar [1, 4, 6] [2, 3, 4, 7] = [1,2,3,4,4,6,7]
Ejercicio 4
¿Cuáles de las siguientes relaciones son funciones? En caso de que la relación sea función, clasifícala.
Justifica.
2 x`
R3
^ x, y / x, y  N u N š y
^ x, y / x, y  N u N š y
^ x, y / x, y  N u N š y
R4
^ x, y / x, y  Z u N š y
x2`
R1
R2
Ejercicio Nº 5
Sea la función
x`
x 1`
f x
f :RoR /
5 x 8
3
9
a) Demuestra que f es biyectiva
b) Halla la función inversa de f
c) Sea la función g : R o
Calcula
f
Ejercicio Nº 6
R /
g x
2x 9
D g (5)
Analiza la veracidad de las siguientes afirmaciones.
Si es cierta, demostrarla. Si es falsa, dar un contraejemplo.
a)
A Ž B y C Ž D Ÿ A ˆ C Ž B ˆ D
b)
A ˆ B A
‡
Profesores: Patricia Echenique, Saúl Tenenbaum