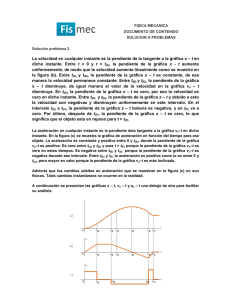
1 1 kt v v = +

Movimiento en el plano
Problema # 2.15
2.15.- Después de para el motor de una canoa, ésta tiene una aceleración en sentido
opuesto a su velocidad y directamente proporcional al cuadrado de ésta; osea, que se
dv
puede escribir
 kv 2 , donde k es constante. Supongamos que se paró el motor
dt
cuando la velocidad era de 6,0 metros por segundo y que la velocidad disminuye hasta
3,0 metros por segundo en un tiempo de 15,0 segundos. ( a) Demostrar que la velocidad v
en el instante t después de para el motor está dada por la relación matemática siguiente:
1 1
  kt
v v0
( b ) Calcular el valor de k. ( c ) Encontrar la aceleración en el instante en que se para el
motor. ( d) Demostrar que la distancia recorrida en un tiempo t es igual a:
1
x   ln  v0  k  t  1
k
( e) Demostrar que la velocidad después de recorrer una distancia x es igual a:
v  v0  e  k  x
Solución:
(a)
a
dv
  kv 2
dt
dv
 kdt
v2
v
t
dv
 1


v0 v 2 0 kdt   v  v  kt
0
v
1  1
1 1
      kt  
v  v0 
v0 v
Luego
1 1
  kt
v v0
(b)
Aplicando la fórmula anterior
FVR (23/01/2007)
Problemas de Física
1
Movimiento en el plano
Problema # 2.15
1 1
  k  15
3 6
1
k
90
(c)
a  kv 2
a
 m 
1
2
  6   0, 4 
2 
90
seg


(d)
1 1
  kt
v v0
1 1  kv0t

v
v0
v
v0
dx

dt 1  kv0t
dx 

x
0
v0 dt
1  kv0t
v0 dt
0 1  kv t
0
dx  
x
t
1
 ln  kv0t  1
k
(e)
FVR (23/01/2007)
Problemas de Física
2
Movimiento en el plano
Problema # 2.15
kx  ln  kv0t  1
Tomando antilogaritmo y dividiendo ambos lados de la ecuación por v0
ekx kv0t  1 1


v0
v0
v
De donde:
v0
v  kx  v0e kx
e
FVR (23/01/2007)
Problemas de Física
3