Document

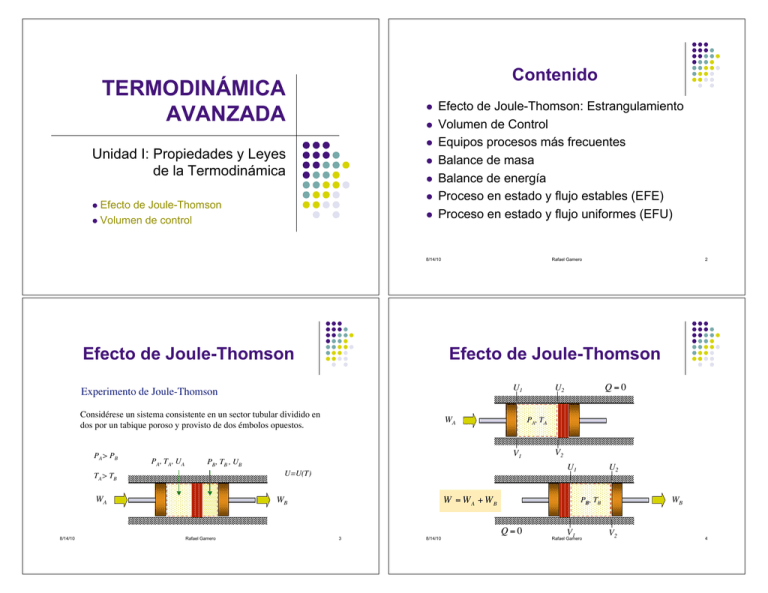
Contenido
TERMODINÁMICA
AVANZADA
!
!
!
Unidad I: Propiedades y Leyes
de la Termodinámica
!
!
!
Efecto de Joule-Thomson
! Volumen de control
!
!
Efecto de Joule-Thomson: Estrangulamiento
Volumen de Control
Equipos procesos más frecuentes
Balance de masa
Balance de energía
Proceso en estado y flujo estables (EFE)
Proceso en estado y flujo uniformes (EFU)
8/14/10
Efecto de Joule-Thomson
Rafael Gamero
Efecto de Joule-Thomson
U1
Experimento de Joule-Thomson
Considérese un sistema consistente en un sector tubular dividido en
dos por un tabique poroso y provisto de dos émbolos opuestos.
PA > P B
PA , T A , U A
V1
!
V2
U1
W = WA + WB
WB
Rafael Gamero
Q=0
U2
PA , T A
U=U(T)
WA
8/14/10
WA
PB, TB , UB
TA> TB
2
3
!
!
WB
PB, TB
Q=0
8/14/10
U2
V1
Rafael Gamero
V2
4
Efecto de Joule-Thomson
Efecto de Joule-Thomson
Experimento de Joule-Thomson
Experimento de Joule-Thomson
"U = Q + W
Q=0
W = "P (V2 " V1 )
!
!
"P (V2 " V1 ) A " P (V2 " V1 ) B = (U 2 " U1 ) A + (U 2 " U1 ) B
"U = W
W = WA + WB
!
"U = "U A + "U B
8/14/10
U A + PAVA = U B + PBVB
Característico de los
procesos irreversibles de
expansión
!
"P (V2 " V1 ) A " P (V2 " V1 ) B = (U 2 " U1 ) A + (U 2 " U1 ) B
!
!
Proceso isentálpico:
!
"U A + "U B = W A + W B
!
!
PAVA " PBVB = "U A + U B
Rafael Gamero
HA = HB
H = cte
"H = 0
!
5
8/14/10
Rafael Gamero
!
!
!
6
!
Efecto de Joule-Thomson
Efecto de Joule-Thomson
Diferencial total de entalpía
Diferencial total de entalpía
El diferencial total de la entalpía describe la variación de esa
propiedad con la temperatura y la presión.
Si en un proceso de estrangulamiento la entalpía es constante:
"H = 0
(
)
f H,P,T = 0
H = H (T,P )
8/14/10
Rafael Gamero
#" H &
#" H &
% !
( dT + %
( dP = 0
$ "T ' P
$ "P 'T
!
#"H &
#"H &
dH = %
dT + %
(
( dP
$ "!T ' P
$ "P 'T
!
dH = 0
µJ
7
Coeficiente de Joule-Thomson
8/14/10
!
Rafael Gamero
!
!
!
#" H &
%
(
# "T &
$ "P 'T
= µJ
% ( =)
#" H &
$ "P ' H
%
(
$ "T ' P
8
Efecto de Joule-Thomson
Efecto de Joule-Thomson
Coeficiente de Joule-Thomson
Coeficiente de Joule-Thomson
Un coeficiente de Joule-Thomson con signo positivo significa que la
temperatura del fluido disminuye durante el estrangulamiento.
El estrangulamiento es un proceso de expansión irreversible cuando
un fluido pasa por un paso restringido representado por el tabique del
sistema mostrado inicialmente.
Un coeficiente de Joule-Thomson con signo negativo significa que la
temperatura del fluido aumenta durante el estrangulamiento.
# "T &
µJ = % (
$ "P ' H
Aproximación
discreta, para usar
e.g. la tabla
termodinámica.
8/14/10
$T #T '
µJ " & 2 1 )
% P2 # P1 ( h
H = cte
Rafael Gamero
!
El proceso ocurre en el paso del fluido a través de válvulas de
expansión.
9
8/14/10
H = cte
Rafael Gamero
10
!
Volumen de Control
Equipos de Procesos
El sistema abierto
Equipos de transferencia de calor
Los sistemas se clasifican en cerrados y abiertos.
también se denominan volumen de control.
El estudio de efectos energéticos en
procesos industriales se efectúan por
volumen de control.
8/14/10
Calderas:
Equipos de
generación de vapor
para transporte de
energía
˙ s2 es2
m
W˙
˙
m
! e1 !
ee1
Sistema abierto
(volumen de control)
Estos últimos
!Q
˙
!
!
Rafael
! Gamero
!
!
!
m(t)
E(t)
!
!
˙ e 2 e!e 2
m
˙ s1
m
es1
La energía transportada
mediante vapor puede
ser utilizada para
transferencia de calor o
generación de potencia.
11
8/14/10
Rafael Gamero
12
Equipos de Procesos
Equipos de Procesos
Equipos de transferencia de calor
Equipos de transferencia de calor
Interior de una caldera
acuatubular o con agua en los
tubos
En una planta industrial puede haber más de una caldera para generar el
vapor requerido en los procesos térmicos.
Tubos con flujo de agua
Gase de combustión
entre los tubos
Flama generada por
atomización
8/14/10
Batería de calderas acuatubulares (agua en los tubos)
Rafael Gamero
13
8/14/10
Equipos de Procesos
Rafael Gamero
14
Equipos de Procesos
Equipos de transferencia de calor
Equipos de transferencia de calor
Batería de calderas
pirotubulares
8/14/10
Caldera pirotubular o de fuego en los tubos
Rafael Gamero
15
8/14/10
Rafael Gamero
16
Equipos de Procesos
Equipos de Procesos
Equipos de transferencia de calor
Equipos de transferencia de calor
Corte de una caldera
pirotubular
Válvula de
seguridad
Funcionamiento de una calera
Salida de vapor saturado
Vapor saturado
Vapor sobrecalentado
Tambor de vapor
Coraza con agua
Agua en ebullición
Tubos con gases
de combustión
Tubo descendente
Flama generada por
combustión de
combustible atomizado
8/14/10
Rafael Gamero
Tubos de agua
Agua
Combustible
17
8/14/10
Caldera acuatubular
Tambor de
alimentación de agua
Rafael Gamero
18
Equipos de Procesos
Equipos de generación de potencia
Condensadores:
Turbinas:
Transferencia de calor
para condensar un vapor
Intercambiadores de calor:
Sobrecalentador
Quemador
Equipos de Procesos
Equipos de transferencia de calor
Gas exhausto
Equipos de generación de potencia mediante la transformación de energía contenida
en un vapor o gas a trabajo de árbol (movimiento giratorio).
Calentamiento o enfriamiento de
un fluido
Condensador de tubo y
coraza
Intercambiador de tubo y
coraza
8/14/10
Intercambiador de placas
Rafael Gamero
19
8/14/10
Turbina de gas
Detalle del eje y álabes de una turbina
Rafael Gamero
20
Equipos de Procesos
Equipos de Procesos
Equipos de generación de potencia
Equipos de transporte de fluidos
Una turbina industrial de
vapor generalmente
requiere vapor
sobrecalentado, lo que
garantiza un alto
contenido energético
capaz de generar
potencia suficiente para
realizar trabajo mecánico
a gran escala.
8/14/10
Rafael Gamero
Instalaciones de una
turbina de vapor de una
planta de generación de
energía eléctrica
21
Bombas:
Equipos para mover un líquido aumentando la
presión de flujo.
Bomba centrífuga
8/14/10
Rafael Gamero
Equipos de Procesos
22
Equipos de Procesos
Equipos de transporte de fluidos
Equipos de almacenamiento de fluidos
Compresores:
Tanques:
Equipos para move un gas aumentando la presión de
flujo.
Equipos para
almacenamiento,
transporte, o procesos
de transferencia de
masa con
transferencia de calor
por lotes (batch).
Compresor reciprocante
Tanque
enchaquetado
Compresor rotatorio
8/14/10
Rafael Gamero
23
Tanque con
serpentín
8/14/10
2
2
Rafael Gamero
24
Producción de Potencia
Producción de Potencia
Ciclo de potencia Rankine
Ciclo de potencia Rankine con reactor nuclear
Generador de
vapor
Turbina
Generador
Agua de
enfriamiento
Condensador
Reactor
8/14/10
Rafael Gamero
25
Bomba del condensado
Bomba del agua de reacción
8/14/10
Equipos de Procesos
Rafael Gamero
26
Equipos de Procesos
Simbología y condiciones para los equipos y dispositivos
Simbología y condiciones para los equipos y dispositivos
P = cte
P = cte
2
1
2
Condensador
1
b
P = cte
W
P1>P2
Q=0
a
W
Q=0
2
P = cte
1
2
1
1
2
2
Intercambiador
8/14/10
Evaporador
Rafael Gamero
P1>P2
Turbina
Caldera
27
8/14/10
1
Cilindro-pistón con flujo
Rafael Gamero
28
Equipos de Procesos
Equipos de Procesos
Simbología y condiciones para los equipos y dispositivos
2
Simbología y condiciones para los equipos y dispositivos
Q=0
W
P1<P2
Q=0
Q=0
W
P1<P2
P1<P2
Q=0
1
Bombas
2
P1<P2
1
Compresor rotatorio
W=0
H = cte
H = cte
Compresor reciprocante
Tanque
Válvulas
8/14/10
Rafael Gamero
29
8/14/10
Rafael Gamero
Balances de Masa y Energía
Balance de Masa
Balances en un volumen de control
Tiempo t
Para poder comprender las ecuaciones de balance en un volumen
de control, se toma arbitrariamente un espacio a través del cual
fluye un fluido con propiedades conocidas (medibles y/o
calculables) a la entrada y a la salida de dicho espacio.
To
Pi
!
ei
vi
31
8/14/10
Po
m( t ) =!mvc
E ( t ) = E vc
mi
Este análisis se realiza en un intervalo de tiempo !t.
Rafael Gamero
W vc
Ti
También se establece la relación de calor y trabajo que
interactúan con el volumen de control a través de la superficie de
control, que constituye sus límites.
8/14/10
30
!
!
32
!
!
eo
vo
!
Q
Rafael Gamero
!
mo
Balance de Masa
Tiempo t + !t
W vc
To
Pi
Po
m( t ) =!mvc
E ( t ) = E vc
ei
!
!
vi
8/14/10
(m )
i
mo
eo
Rafael Gamero
!
(m
!
t + "t
t + "t
!
# ( mi ) = m t + "t # m t
t
#m
(
!
) + [(m )
t vc
o
tiempo t + "t
tiempo t
t + "t
) + (m )
o
vc
t + "t
] [
# (mo ) # ( mi )
t
# (mo )
!t
]
t + "t
# ( mi ) = 0
t + "t
# ( mi )
t
Dividiendo la expresión entre !t:
vo
!
Q
[ Entrada] = [ Acumulación] + [Salida]
Balance de masa en el
inervalo de tiempo !t
trancurrido:
Ti
mi
!
Balance de Masa
(m
!
33
!
t + "t
#m
"t
8/14/10
) + [(m )
o
t vc
t + "t
# (mo )
"t
t
] # [(m )
i
Rafael Gamero
"t
t
] =0
34
!
!
Balance de Masa
Balance de Energía
Aplicando límite cuando !t tiende a cero:
%m
$m
t
lim' t + "t
"t #0'
"t
&
(
)
Tiempo t
(
%m
( o ) t + "t $ (mo ) t (* %'(mi ) t + "t $ (mi ) t (*
vc *
+ lim'
$ lim
=0
* "t #0'
* "t #0'
*
"t
"t
&
)
&
)
)
Ti
!
n
" dm %
dmo n dmi
)(
=0
$ ' +(
dt
# dt & vc i=1 dt
i=1
8/14/10
!
Rafael Gamero
ei
vi
Ecuación de continuidad
35
8/14/10
Po
m( t ) =!mvc
E ( t ) = E vc
mi
• Considerando que puede haber más de una entrada y más de una salida:
!
To
Pi
" dm %
d (mo ) d( mi )
(
=0
$ ' +
dt
dt
# dt & vc
!
W vc
!
!
36
!
!
eo
vo
!
Q
Rafael Gamero
!
mo
Balance de Energía
Tiempo t + !t
W vc
To
Pi
Po
m( t ) =!mvc
E ( t ) = E vc
ei
vi
!
!
mo
t
!
eo
(
Rafael Gamero
!
t + "t
(
)
# ( miei ) = E t + "t # E t + ( moeo )
# ( moeo )
t + "t
t
vc!
! t
Qt + "t + tW t + "t = E t + "t # E t
) + [(m e )
o o
vc
t + "t
] [
# ( moeo ) # ( miei )
t
t + "t
# ( m ie i )
t
]
Dividiendo la expresión entre !t:
!
t
8/14/10
tiempo t + "t
tiempo t
!
t Qt + "t + tW t + "t + ( m iei )
vo
!
Q
[ Entrada] = [ Acumulación] + [Salida]
Balance de energía en el
inervalo de tiempo !t
trancurrido:
Ti
mi
!
Balance de Energía
37
8/14/10
!
(
E
#E
Qt + "t tW t + "t
t + "t
t
+
=
"t
"t
"t
) + [( m e )
o o
vc
Rafael Gamero
t + "t
# ( moeo )
"t
t
] # [( m e )
i i
t + "t
# ( m ie i )
"t
t
]
38
!
!
Balance de Energía
Balance de Energía
Aplicando límite cuando !t tiende a cero:
+ E
*E
$ Q
W '
t
lim& t t + "t + t t + "t ) = lim- t + "t
"t #0% "t
"t ( "t #0"t
,
(
!
)
n
n
" dE %
eo dmo
e dm *Q *W
)( i i =
+
$ ' +(
dt
dt
dt
dt
dt
# & vc i=1
i=1
.
+me
( o o ) t + "t * (moeo ) t .0 +-(miei ) t + "t * (miei ) t .0
vc 0
+ lim* lim
0 "t #00 "t #00
"t
"t
,
/
,
/
/
!
d ( moeo ) d ( miei )
"Q "W # dE &
+
=% ( +
)
dt
dt $ dt ' vc
dt
dt
W = W vc + W flujo
n
" dE %
dmo n dmi *Q *W vc *W flujo
) ( ei
=
+
+
$ ' + ( eo
dt
dt
dt
dt
dt
# dt & vc i=1
i=1
!
!
!
• Considerando que puede haber más de una entrada y más de una salida y
• Que la energía e es constante en cada punto.
"W flujo $
dm
dm '
= &(#Pov o ) o + ( Piv i ) i )
dt
dt
dt (
%
!
W flujo = " # PdV
"W flujo = #Pd ( mv )
"W flujo
dm
= #Pv
dt
dt
!
n
" dE %
eo dmo n ei dmi *Q *W
)(
=
+
$ ' +(
dt
dt
dt
# dt & vc i=1 dt
i=1
8/14/10
!
Rafael Gamero
n
dmo n
dm *Q !*W vc +
dm
dm .
! " dE %
) ( ( ui + eci + e pi ) i =
+
+ -()Pov o ) o + ( Piv i ) i 0
$ ' + ( ( uo + eco + e po )
dt
dt
dt
dt
dt
dt /
,
# dt & vc i=1
i=1
39
8/14/10
!
Rafael Gamero
40
Balance de Energía
Procesos EFE y EFU
n
" dE %
dmo n
dm *Q *W vc
) ( ( ui + eci + e pi + Piv i ) i =
+
$ ' + ( ( uo + eco + e po + Pov o )
dt
dt
dt
dt
# dt & vc i=1
i=1
Los procesos en un volumen de control pueden ser de dos
tipos:
• En estado estacionario:
Proceso en estado y flujo estable (EFE)
Ecuación desarrollada de Primera Ley
!
n "
n "
" dE %
v 2o
g % dm
v2
g % dm *Q *W vc
+ z o ' o ) ($ h i + i + z i ' i =
+
$ ' + ($ h o +
2gc gc & dt
2gc gc & dt
dt
dt
# dt & vc i=1 #
i=1 #
!
Donde la energía total E es:
Ejemplo: Claderas, intercambiadores, condensadores, bombas,
turbinas y compresores.
• En estado no estacionario:
Proceso en estado y flujo uniforme (EFU)
E = U + Ec + E p
Ejemplo: Tanques durante el llenado o descarga, reactores tipo batch.
8/14/10
Rafael Gamero
41
8/14/10
Rafael Gamero
42
!
Estado Estacionario
n
" dm %
dmo n dmi
)(
=0
$ ' +(
dt
# dt & vc i=1 dt
i=1
Estado Estacionario
Ecuación de continuidad
n
n
•
•
"m # "m
o
i=1
i
=0
Ecuación de continuidad para procesos de
estado y flujo estables (EFE).
i=1
Ecuación de Primera Ley
!
n "
n "
" dE %
v 2o
g % dm
v2
g % dm *Q *W vc
+ z o ' o ) ($ h i + i + z i ' i =
+
$ ' + ($ h o +
2gc gc & dt
2gc gc & dt
dt
dt
# dt & vc i=1 #
i=1 #
!
Ecuación de Primera Ley para procesos de estado y flujo estables (EFE).
n
!
" dm %
$ ' =0
# dt & vc
En estado estacionario:
8/14/10
Rafael Gamero
!
i=1
43
!
"
($ h
" dE %
$ ' =0
# dt & vc
8/14/10
!
#
o
+
n "
•
•
v 2o
g %•
v2
g %•
+ zo ' m o ) ($ hi + i + zi ' m i = Q+ W vc
2gc gc &
2gc gc &
i=1 #
Rafael Gamero
44
Estado no Estacionario
n
" dm %
dmo n dmi
)(
=0
$ ' +(
dt
# dt & vc i=1 dt
i=1
Estado no Estacionario
Ecuación de continuidad
n
(m
2
n
" m1 ) vc + # mo " # mi = 0
i=1
Ecuación de continuidad para procesos de
estado y flujo uniformes (EFU).
i=1
Ecuación de Primera Ley
!
n "
n "
" dE %
v 2o
g % dm
v2
g % dm *Q *W vc
+ z o ' o ) ($ h i + i + z i ' i =
+
$ ' + ($ h o +
2gc gc & dt
2gc gc & dt
dt
dt
# dt & vc i=1 #
i=1 #
!
Ecuación de Primera Ley para procesos de estado y flujo uniformes (EFU).
Multiplicando ambas ecuaciones por dt e integrando:
n t
t "
t n
dm %
dm
dm
E.g.: Ecuación de continuidad:
( $# dt '& dt + ( ) dt o dt * ) ( dt i dt = 0
0
0 i=1
i=1 0
vc
!
8/14/10
Rafael Gamero
(E
45
2
r
r
n
$
$
#2
g ' n
#2
g '
" E1 ) vc + * mo & ho + o + zo ) " * mi & hi + i + zi ) = Q + W vc
2gc gc ( i=1 %
2gc gc (
%
i=1
8/14/10
Rafael Gamero
46
!
!
Estado no Estacionario
Volumen de Control
Selección de un volumen de control
n
" dm %
dmo n dmi
)(
=0
$ ' +(
dt
# dt & vc i=1 dt
i=1
Ecuación de continuidad
t
" dm %
( $# dt '&
!
0
t
dt +
vc
El volumen de contro se puede seleccionar según las condiciones
medibles en el proceso.
n
n t
dmo
dmi
dt * ) (
dt = 0
dt
dt
i=1
i=1 0
()
0
2
(
)
(
)
n d " xoA
n d " xiA
o
o
i
i
d
!$ #
=0
("V ) vc + #
dt
dt
dt
i=1
i=1
!
d
dt
8/14/10
!
n
n
### vc "dV + % ## sc "o$ odAo & % ## sc "i $ i dAi = 0
i=1
i=1
Rafael Gamero
W
Turbina
Caldera
Ecuación de continuidad en
función de propiedades
locales del fluido
47
8/14/10
1
Rafael Gamero
3
48