u.2.

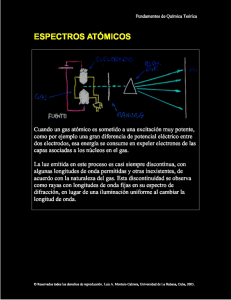
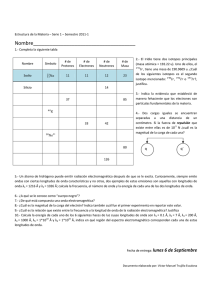
ANTARES - Módulo 2 - Unidad 2 - Programa de Nuevas Tecnologías - MEC
Unidad didáctica 2:
Espectros estelares
Espectros observados de estrellas
file:///F|/antares/modulo2/m2_u200.html [12/3/2000 17.09.01]
ANTARES - Módulo 2 - Unidad 2-01- Programa de Nuevas tecnologías - MEC -
2.1. Radiación electromagnética y espectros
Naturaleza de la luz
● Unidades: Angstrom
●
Líneas espectrales
●
El fotón
●
Líneas de emisión
●
Líneas de absorción
Figura 2-2-1: Espectrógrafo
Cuando la luz pasa a través de un prisma se descompone en bandas de
colores como el arco iris. Así la "luz blanca" se compone de todos los colores
del arco iris y en un cierto orden que siempre es el mismo, rojo, anaranjado,
amarillo, verde, azul, índigo y violeta (Figura 2-2-1). Podemos entender porque
la luz contiene los diferentes colores si pensamos que la luz son ondas
electromagnéticas que viajan a la velocidad de 300 000 km/s, este valor se
conoce como la velocidad de la luz. La distancia entre dos crestas sucesivas
de la onda se denomina la longitud de onda. Luz de diferentes longitudes de
onda aparece como de diferentes colores. La luz roja tiene una vez y media la
longitud de onda de la luz azul y la luz amarilla tiene una longitud de onda
intermedia entre las dos.
file:///F|/antares/modulo2/m2_u201.html (1 de 4) [12/3/2000 17.09.03]
ANTARES - Módulo 2 - Unidad 2-01- Programa de Nuevas tecnologías - MEC -
Unidades: el Angstrom
Las longitudes de onda de la luz son muy cortas, unas pocas centésimas o
milésimas de un centímetro, por ello los astrónomos usan una unidad de
longitud de onda llamada Angstrom, 1 Å es 10-8 cm o bien en nanometros
(1nm = 10-9m) 1 Å es 10-1 nm. Por ejemplo: la longitud de onda de la luz violeta
es aproximadamente 4000 Å , y la de la amarilla 6000 Å . El ojo no es sensible
a radiaciones de longitud de onda más corta que 4000 Å ni más larga que 6500
Å pero hay instrumentos que pueden medir la luz a más cortas y mas largas
longitudes de onda. La radiación más corta que el violeta es la ultravioleta y
rayos X, a longitudes mayores que el rojo está el infrarrojo, y las radio ondas.
Desde un punto de vista científico no hay diferencias cualitativas reales entre
las radiaciones de diferentes longitudes de onda, se denominan ondas
electromagnéticas y las ondas de luz están comprendidas en un rango
limitado. Cuando una onda electromagnética tiene una longitud de 1Å , se
llama rayos X. Cuando tiene 5 000 Å la llamamos luz y cuando tiene una
longitud de onda de 1 cm se denomina radio onda. Naturalmente hay
diferencia en el método de detectar estas radiaciones pero el principio que
gobierna su existencia es el mismo.
Líneas espectrales
El primero que mostró que la luz del Sol contenía los colores del arco iris fué
Newton en 1666, más tarde Fraunhofer en 1811 estudió la luz del Sol
haciéndola atravesar un prisma y vió que se descomponía en colores pero
que en ciertos colores había huecos que parecian líneas oscuras. Estos
huecos se llaman líneas espectrales y el fondo de colores sobre el que se
superponen los huecos se denomina el espectro continuo. Las líneas oscuras
del espectro del Sol, y del espectro de la mayoría de las estrellas, representan
una disminución de la radiación electromagnética a unas longitudes de onda
particulares y se denominaba líneas de absorción. También es posible que a
ciertas longitudes de onda a veces haya más radiación que en las longitudes
de onda próximas, apareciendo como huecos brillantes, reciben entonces el
nombre de líneas de emisión. El químico alemán Gustav Kirchhoff descubrió
en 1859 que las líneas espectrales pueden explicarse como la absorción o
emisión de energía, a una determinada longitud de onda, producida por los
átomos de un elemento químico que se encuentra en estado gaseoso. Un
átomo está constituido por un núcleo rodeado de partículas orbitantes,
llamadas electrones. Las partículas del núcleo son los protones que tienen
una unidad de carga eléctrica positiva, y los neutrones que no tienen carga
eléctrica. Los electrones tienen una unidad de carga eléctrica negativa y son
1800 veces menos masivos que los protones o los neutrones. Según la
mecánica cuántica un átomo sólo puede tener ciertos valores discretos de
energía, es decir, no son posibles todos los valores de la energía, se dice que
los estados de energía de un átomo están cuantificados.
Naturaleza de la luz: el fotón
file:///F|/antares/modulo2/m2_u201.html (2 de 4) [12/3/2000 17.09.03]
ANTARES - Módulo 2 - Unidad 2-01- Programa de Nuevas tecnologías - MEC -
Cuando un átomo pasa de un estado de energía superior a uno inferior, la
diferencia de energía entre los dos estados es emitida en forma de radiación,
llamada también fotones. Un fotón se considera como una partícula de
radiación electromagnética y de aquí la doble dualidad de la luz (y toda la
radiación electromagnética) que tiene propiedades de ondas en algunas
circunstancias y propiedades de partículas bajo otras circunstancias. Los
fotones naturalmente viajan a la velocidad de la luz. Una relación entre la
dualidad onda corpúsculo de la luz se ve claramente en la relación entre la
energía del fotón (partícula),E, y su longitud de onda (onda),λ,
E = h c/λ = h ν donde h es la constante de Planck (6.6256 x 10-34 J), c la
velocidad de la luz (300 000 km. s-1) y ν es la frecuencia de la radiación que es
inversamente proporcional a la longitud de onda, ν = c/λ. Un fotón muy
energético, por ejemplo un fotón de rayos X, tiene una longitud de onda muy
pequeña, 1 Å, un fotón de luz visible tiene menos energía pero una longitud de
onda mayor, 5000 Å .
Líneas de emisión
Cuando se calienta un gas sus átomos se encuentran en estados de energía
superiores al estado más bajo de energía posible (llamado estado
fundamental), se dice que los átomos están excitados. Pero los átomos sólo
pueden permanecer en estados excitados un cierto tiempo, llamado vida
media, al cabo del cual espontáneamente se desexcitan pasando al
fundamental y emitiendo fotones. Estos fotones representan energía a ciertas
longitudes de onda que corresponde en el espectro a longitudes de onda
brillantes, es decir, líneas de emisión.
Líneas de absorción
Cuando la radiación continua (energía emitida a todas las longitudes de onda
o frecuencias) de un cuerpo a una temperatura alta, pasa a través de un gas
frío, los átomos constituyentes del gas atrapan energía de la radiación
continua y se excitan a estados superiores de energía. En el espectro
observamos menos energía, la robada por los átomos, a ciertas longitudes de
onda, son las líneas de absorción que en el visible aparecen como líneas
oscuras. Las líneas de absorción no pueden formarse sin que exista una
fuente que emita un continuo ( radiación continua), por el contrario las de
emisión sí.
Cuando suministramos energía a un átomo y se excita, uno o más de sus
electrones orbitales pasa a un nivel superior de energía, puede ocurrir que la
energía suministrada se tal que permita al electrón escaparse del átomo.
Cuando ocurre esto decimos que el átomo se ioniza y el remanente que
queda, un átomo con menos electrones, recibe el nombre de ión. Si sólo
pierde un electrón se dice un átomo una vez ionizado, si pierde dos electrones
es un átomo dos veces ionizado y así sucesivamente.
Resumiendo lo anterior podemos decir que: sí un vapor de un elemento
cualquiera se calienta, produce un conjunto característico de líneas de
emisión, que ese elemento y sólo él posee esas líneas espectrales
específicas. Por otro lado, si un espectro continuo radiado por una fuente de
energía a alta temperatura pasa a través de un vapor frío de cualquier
file:///F|/antares/modulo2/m2_u201.html (3 de 4) [12/3/2000 17.09.03]
RECUERDA
Si un vapor de un
elemento
cualquiera se
calienta, produce un
conjunto
característico de
líneas de emisión,
que ese elemento y
sólo él posee esas
líneas espectrales
específicas
Si un espectro
continuo radiado
por una fuente de
energía a alta
temperatura pasa a
través de un vapor
frío de cualquier
elemento, aparece
un conjunto de
líneas de absorción
superpuestas al
espectro continuo y
estas líneas de
absorción tienen las
mismas longitudes
ANTARES - Módulo 2 - Unidad 2-01- Programa de Nuevas tecnologías - MEC -
elemento, aparece un conjunto de líneas de absorción superpuestas al
espectro continuo y estas líneas de absorción tienen las mismas longitudes
de onda características de las líneas de emisión de ese elemento químico. Así
el vapor de un elemento a través del que ha pasado la luz ha substraído
energía del espectro continuo a las longitudes de onda que son propias del
elemento. Sí un espectro continuo pasa a través de un vapor de un elemento y
después a través de otro vapor de un elemento diferente, o a través de una
mezcla de los dos gases, el espectro de absorción que resulta muestra las
líneas de absorción características de ambos elementos.
El espectro de la mayoría de las estrellas muestra un continuo y superpuestas
líneas de absorción que corresponden a los mismos elementos que se
observan en el laboratorio, luego estos son los constituyentes de las capas
exteriores de las estrella, que absorben la radiación continua generada en el
interior de la estrella, y producen la formación de las líneas de absorción. El
espectro de absorción de una estrella sirve pues a identificar los elementos
químicos constituyentes de su atmósfera, ya que cada elemento produce sus
propias líneas de absorción. Si un elemento químico está presente en gran
cantidad sus líneas espectrales características serán muy intensas, pero la
observación del espectro sólo nos indica los elementos presentes pero no
sus abundancias relativas, ya que la intensidad de las líneas depende no sólo
de la abundancia sino también de la temperatura a la que se encuentra el
elemento que produce la absorción, la observación de los espectros estelares
puede suministrar información sobre la temperatura y otras condiciones
físicas de las atmósferas estelares.
file:///F|/antares/modulo2/m2_u201.html (4 de 4) [12/3/2000 17.09.03]
de onda
características de
las líneas de
emisión de ese
elemento químico
ANTARES - Módulo 2 - Unidad 2-02- Programa de Nuevas tecnologías - MEC -
2.2. El cuerpo negro
●
Ley de Stefan-Boltzmann
●
Función de Planck
●
Ley de desplazamiento de Wien
Observando a simple vista las estrellas se puede notar que tienen diferentes
colores. El color del Sol es amarillo mientras que Sirio, que es la estrella más
brillante de nuestro Hemisferio, es blanca. La mayoría de las estrellas tienen
un color más rojizo que el Sol. Esta diferencia de color puede informara sobre
la naturaleza de las estrellas y se explica, como vamos a ver, por la diferencia
de temperaturas superficiales. Podemos comparar los colores de las estrellas
con los de una fuente ideal de luz, cuyas propiedades dependan sólo de un
parámetro, tal fuente es el cuerpo negro cuya radiación depende sólo de la
temperatura.
¿Qué es un cuerpo negro? Podemos llamar a un objeto negro si parece negro
a la luz del día, esto significa que el objeto no envía ningún rayo de luz a
nuestros ojos. La luz que recibimos de los objetos, que no parecen negros a
la luz del día, no es luz que los objetos emiten sino sólo luz solar reflejada por
ellos. La razón de la diferencia en color es que algunos objetos absorben
parte de la luz solar y sólo la parte no absorbida puede reflejarse. Si se
absorbe principalmente el azul, entonces los objetos parecerán más rojos que
el Sol, si se absorben las longitudes de onda rojas el objeto parecerá más
azul. Si todas las longitudes de onda se absorben, no queda luz para
reflejarse, y el objeto parecerá negro. Definimos un cuerpo negro como un
objeto que absorbe toda la luz que le llega. Esto no significa que un cuerpo
negro siempre parezca negro, un cuerpo negro puede generar radiación por si
mismo, y ser bastante brillante aún cuando absorba toda la luz que le llega.
Por ejemplo, la placa caliente de una cocina eléctrica, si está apagada parece
negra porque absorbe toda la luz que le llega, pero cuando se enciende y se
calienta produce su propia luz y brilla aunque se apaguen todas las luces
exteriores. La placa caliente es todavía un cuerpo negro porque absorbe casi
todas la luz que le llega pero ya no parece negra, cuando ponemos la placa en
el mínimo la vemos de color rojo conforme aumentamos la temperatura se
hace más brillante y amarilla, en el máximo la placa se hace más brillante y
más azul. Con este ejemplo vemos que el color de un cuerpo negro nos
informa de la temperatura que tiene.
Ley de Stefan-Boltzmann
file:///F|/antares/modulo2/m2_u202.html (1 de 3) [12/3/2000 17.09.04]
ANTARES - Módulo 2 - Unidad 2-02- Programa de Nuevas tecnologías - MEC -
En Física llamamos un cuerpo negro a aquel que se encuentra en equilibrio
termodinámico, tiene temperatura constante y la radiación que emite es
siempre la misma sino cambia la temperatura, es decir, la radiación emitida
depende de la temperatura. Para altas temperaturas, más radiación se emite y
parece más azul. Si medimos la radiación de un cuerpo negro encontramos
que la energía radiativa total E emitida por m2 y por segundo, en todas las
direcciones por un cuerpo negro de temperatura T, aumenta con la cuarta
potencia de la temperatura que es la ley de Stefan-Boltzmann, σ T4 . La
cantidad de energía que emite un cuerpo negro por m2 cada segundo en todas
las direcciones y a todas las longitudes de onda se denomina el flujo, πF
E = σ T4 = πF
donde σ es la constante de Stefan-Boltzmann σ = 2p 5 k4 / 15c2 h3 = 5.67 x
10-5 erg cm-2 s-1 K-4 = 5.67 x 10-8 W m-2 K-4 y F es el flujo en W m-2 .
La ley de Stefan-Boltzmann también se expresa como πB(T) = σ T4 donde
B(T) es la función de Planck integrada para todas las frecuencias o longitudes
de onda.
Función de Planck
Podemos medir la cantidad de radiación por intervalo de longitud de onda por
unidad de superficie y dentro de un ángulo sólido unidad emitida por un
cuerpo negro, entonces esta energía se conoce como la función de Planck y
nos da la distribución de energía de un cuerpo negro o distribución de Planck
y sólo depende de la temperatura y de la long. de onda.
Bλ = 2hc2 / λ 5 [1/ (ehc/λkT - 1)]
Bν = 2hν3/c2 [1/(ehν/kT - 1)
donde c = velocidad de la luz (3 x 108 m s-1), k = constante de Boltzmann (1.38
x 10-23 J K-1), y h = constante de Planck (6.63 x 10-34 J s).
Si dibujamos Bλ; (T) frente a λ obtenemos una curva que alcanza un máximo y
cae a cero para muy grandes y muy pequeñas longitudes de onda, lo mismo
ocurre para Bν; (T). La altura de la curva y la longitud de onda del máximo son
funciones de la temperatura, este máximo se obtiene haciendo la derivada de
la función de Planck igual a cero. La longitud de onda, λ max , para la que la
función Bλ; es máxima es la siguiente:
λ max T =
0.29 cm K = 2.9 x 10-3 m K
Ley de desplazamiento de Wien
file:///F|/antares/modulo2/m2_u202.html (2 de 3) [12/3/2000 17.09.04]
ANTARES - Módulo 2 - Unidad 2-02- Programa de Nuevas tecnologías - MEC Figura 2-2-2:
Distribución de
energía de un cuerpo
negro para distintas
temperaturas. El
máximo de la
distribución se
desplaza al variar la
temperatura: Ley de
Wien.
Al variar la temperatura el valor de l max se desplaza, a mayor temperatura en
longitudes de onda menores se presenta el máximo, esta ley se conoce como
ley de desplazamiento de Wien (Figura 2-2-2).
file:///F|/antares/modulo2/m2_u202.html (3 de 3) [12/3/2000 17.09.04]
ANTARES - Módulo 2 - Unidad 2-03- Programa de Nuevas tecnologías - MEC -
2.3. Temperaturas estelares
●
Temperatura efectiva
●
Obtención de radios
●
Temperatura de Wien
Se puede suponer que las estrellas se comportan como cuerpos negros, esta
hipótesis implica que la temperatura y la cantidad luz (flujo: energía por m2 y
segundo) que emite son constantes. Si las estrellas radian como cuerpos
negros se podría deducir su temperatura.
Temperatura efectiva
Sabiendo que la cantidad total de energía emitida por un cuerpo negro sólo
depende de la temperatura, se puede comparar la cantidad de energía emitida
por las estrellas por m2 y por segundo con la del cuerpo negro. La cantidad de
energía emitida por las estrellas por m2 y por segundo es el llamado flujo
superficial πFsurf. Para determinar este flujo medimos la cantidad de energía
que llega a la tierra, corregida de la atmósfera terrestre, por m2 y por segundo
que hemos llamado brillo, b. La luminosidad de la estrella, la energía emitida
por segundo será
L = 4π d2 b
donde d es la distancia a la que se encuentra la estrella. Por otro lado, la
luminosidad en función del flujo superficial emitido por la estrella será el área
de la estrella 4π R2, multiplicada por el flujo emitido por su superficie π Fsurf
(energía por m2 y por segundo) .
L = 4π R2 π Fsurf
igualando las dos expresiones de la luminosidad de una estrella, se obtiene
una relación entre el brillo medido en la Tierra y la cantidad de luz emitida por
la superficie de la estrella.
π Fsurf = b (d/R)2 = b 1/θ 2
donde θ = R/d es semidiametro angular de la estrella que debemos conocerlo
para obtener π Fsurf.
La ley de Stefan-Boltzmann nos define la temperatura efectiva de una estrella
file:///F|/antares/modulo2/m2_u203.html (1 de 3) [12/3/2000 17.09.04]
ANTARES - Módulo 2 - Unidad 2-03- Programa de Nuevas tecnologías - MEC -
σ T4 = π B = π Fsurf = σ T4eff
que es la temperatura de un cuerpo negro que radia la misma cantidad de
energía total que la estrella. Así se define la temperatura efectiva de una
estrella, es la temperatura de un cuerpo negro que emite el mismo flujo total
que la estrella, la energía perdida por la estrella por m2 y por segundo es la
misma que la de un cuerpo negro a T = Teff .
Esta temperatura es la de la superficie de la estrella que es la que emite
principalmente la radiación que recibimos. Se considera, pues que la
temperatura efectiva es la de las capas superficiales (atmósfera, fotosfera)
que son las que contribuyen a la radiación observada
Obtención de radios
Por la definición de temperatura efectiva podemos obtener una nueva
expresión de la luminosidad de la estrella en función de la Teff.
L = 4π R2 πFsurf = 4π R2 σ T4eff
si conocemos la temperatura y la luminosidad podemos obtener el radio. La
luminosidad total viene medida por la magnitud bolométrica absoluta
Mbol - M¤ bol = - 2.5 log L /L¤
Mbol - M¤ bol = - 2.5 log L /L¤ = - 5 log R /R¤ +
10 log Teff / T¤ eff
Recordando que la magnitud bolométrica absoluta la obtenemos a partir de la magnitud absoluta
visual y la corrección bolométrica
Mbol = MV - c.b.
y la magnitud absoluta visual se obtiene a partir de la aparente V y la distancia
Temperatura de Wien
file:///F|/antares/modulo2/m2_u203.html (2 de 3) [12/3/2000 17.09.04]
ANTARES - Módulo 2 - Unidad 2-03- Programa de Nuevas tecnologías - MEC -
La distribución de energía de una estrella se puede usar también para
determinar la temperatura. Podemos usar la ley de desplazamiento de Wien, y
determinar su temperatura calculando la longitud de onda del máximo de su
distribución y como los cuerpos negros se hacen más azules para altas
temperaturas es de esperar que los colores de las estrellas estén relacionados
con sus temperaturas.
Por ejemplo, para un temperatura de 4000 K el máximo de radiación está
situado en 7.2 x 10-5 cm, la longitud del color rojo, luego las estrellas rojas
tienen temperaturas de 3000 a 4000 K. Una estrella amarilla tiene entre 5000 y
6000 K, su máximo cae en el visible. Las estrellas más calientes tienen un
máximo de radiación en la región ultravioleta (UV) del espectro (λ = 3 x 10-5
cm ) que no es perceptible por el ojo humano, en consecuencia sólo
observamos que la intensidad de la radiación disminuye en la región visible.
Para el Sol el máximo está en el visible alrededor de 5000 Å que nos da una
temperatura de unos 6000 K que es muy parecida a la temperatura efectiva,
5780 K. Ambos valores de temperatura obtenidos están en buen acuerdo y es
de esperar que nos indiquen la temperatura de las capas superficiales del Sol
y que su radiación no es muy diferente de la de un cuerpo negro.
Los índices de color también están relacionados con la temperatura
superficial, sí una estrella es muy caliente su radiación tendrá el máximo de la
distribución en longitudes de onda del ultravioleta, lo que implica que será
mas brillante en el filtro U que en el B y mucho más que en el V. Por el
contrario, una estrella fría emitirá más en el filtro V que en el B y en el U.
file:///F|/antares/modulo2/m2_u203.html (3 de 3) [12/3/2000 17.09.04]
ANTARES - Módulo 2 - Unidad 2-04- Programa de Nuevas tecnologías - MEC -
2.4. El efecto Doppler
●
Efecto Doppler
●
Velocidad radial
●
Velocidad tangencial
Efecto Doppler
El efecto Doppler es una herramienta importante para entender el Universo, ya
que sin conocer la distancia a un objeto podemos utilizar el efecto Doppler
para determinar su velocidad radial, que es la velocidad en la dirección de
observación con que el objeto se aleja o se acerca a la Tierra. Si la estrella se
mueve a la misma velocidad que el observador no se detectaría el efecto
Doppler.
El efecto Doppler en el sonido es un hecho conocido en la vida diaria, su
análogo en la radiación electromagnética, incluyendo la luz, es muy similar.
Por ejemplo, en el sonido, el cambio en el pitido del tren cuando se aproxima,
pasa y empieza a alejarse. Al principio el objeto que emite la onda sonora se
está acercando y cuando emite la segunda onda se ha movido más cerca que
cuando emitió la primera onda, así las ondas pasa con más frecuencia que si
la fuente estuviese en reposo, las longitudes de onda parecen comprimirse y
el pitido del tren se hace más fuerte. Cuando la fuente emisora pasa nuestra
posición, las longitudes de onda parecen dilatarse y el pitido disminuye.
Figura 2-2-3: Efecto
Doppler. El emisor de
sonido o luz se mueve
hacia la izquierda
desde S1 hasta S4
emitiendo en cada
posición una onda,
numerada de 1 a 4. La
distancia entre las
ondas es más estrecha
en el sentido del
movimiento y más
ancha en el contrario.
En consecuencia la
observadora percibirá
una longitud de onda, λ
, más corta, un sonido
más agudo y la luz más
azulada. El observador,
por el contrario, vera
como la fuente se aleja,
λ , será más larga, y
por tanto el sonido más
file:///F|/antares/modulo2/m2_u204.html (1 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2-04- Programa de Nuevas tecnologías - MEC grave y la luz más roja.
Figura 2-2-4: Efecto Doppler. Un observador en una nave espacial que se mueve muy
rápida, verá las estrellas delante de él más azules de lo normal mientras que las que
están detrás parecen más rojas. el cambio de color se debe al movimiento de la nave
respecto a las estrellas.
file:///F|/antares/modulo2/m2_u204.html (2 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2-04- Programa de Nuevas tecnologías - MEC -
La radiación visible es así desplazada hacia el azul. Por el contrario si el
objeto emisor se está alejando del observador las longitudes de onda se
hacen más largas y se dice que la radiación se desplaza hacia el rojo (Figura
2-2-3 y 2-2-4). Generalizando a todo tipo de radiación, se dice que se desplaza
hacia el azul si cambia a longitudes de onda más cortas y el objeto emisor se
acerca al observador y por convenio su velocidad es negativa. Por el contrario
decimos que la radiación se desplaza hacia el rojo si cambia a longitudes de
onda mayores y la fuente emisora se aleja con velocidad positiva. Este
desplazamiento es función de la longitud de onda en reposo λ0 y de la
velocidad radial del cuerpo emisor vr. Así la fracción que la longitud de onda
en reposo, λ - λ 0 = ∆ λ , se desplaza es la misma que la fracción de la
velocidad de la luz a la que el cuerpo se mueve, que se escribe ∆ λ /l 0 = vr /c,
donde ∆ λ es el desplazamiento en longitud de onda, λ 0 es la longitud de onda
en reposo, vr la velocidad radial (componente de la velocidad proyectada en la
dirección de observación) del cuerpo emisor y c la velocidad de la luz.
Velocidad radial
Del análisis de los espectros de las estrellas se puede determinar su
velocidad radial, ya que después de identificar las líneas espectrales
comparando con los espectros de laboratorio, se puede medir la posición en
que se observan las líneas, λ obs, que será distinta de la longitud de onda en
reposo o de laboratorio, λ 0 , la diferencia dará, por efecto Doppler, la
velocidad radial. Para medir la posición de las líneas se toman espectros de
comparación de elementos conocidos, antes y después de observar la estrella
problema con el mismo detector. Como el espectro de comparación es
conocido identificamos sus líneas y su posición nos permite obtener la
longitud de onda de las líneas de la estrella. Una vez obtenida las longitudes
de onda de las líneas estelares, su diferencia con las de laboratorio nos da la
velocidad radial, vr de la estrella. Evidentemente para tener los valores
respecto del Sol, que es como se dan en los catálogos, hay que corregir del
movimiento de la Tierra.
Velocidad tangencial
Figura 2-2-5: La
velocidad de una
estrella respecto al
Sol, v, tiene dos
componentes, la
velocidad radial en la
dirección de
observación, vr, y la
componente
perpendicular o
velocidad tangencial,
vt.
file:///F|/antares/modulo2/m2_u204.html (3 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2-04- Programa de Nuevas tecnologías - MEC -
La velocidad de una estrella respecto al Sol, además de la componente en la
dirección de observación o velocidad radial, tiene otra componente en la
dirección perpendicular que se llama velocidad tangencial (Figura 2-2-5). Esta
se obtiene a partir de la velocidad angular o movimiento propio, µ,
multiplicado por la distancia, d,
vt = µ d
El movimiento propio se puede medir tomando placas fotográficas en
intervalos de varios años o décadas y se mide en segundos de arco por año
("/año). Si medimos la distancia en parsecs, para obtener la velocidad
tangencial en km s-1, hay que hacer la transformación de unidades siguiente:
segundos de arco a radianes (1 rad = 206 265"), años a segundos (1 año =
3.156 x 107 s), y parsecs a kilómetros (1 pc = 3.086 x 1013 km). Con este
cambio de unidades obtenemos la siguiente expresión para la velocidad
tangencial,
vt = µ d
vt = 4.74 µ d
La velocidad de la estrella respecto al Sol será
v = (vr2 + vt2)1/2
file:///F|/antares/modulo2/m2_u204.html (4 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2-05- Programa de Nuevas tecnologías - MEC -
2.5. Clasificación espectral
●
Tipos espectrales
En las últimas décadas del siglo XIX se fotografiaron miles de espectros de
estrellas, encontrándose que había muchas diferencias entre ellos y se
empezó a desarrollar una clasificación de los diferentes tipos de espectros.
Annie Jump Cannon de la Universidad de Harvard clasificó más de 500.000
espectros estelares, su trabajo está recogido en el catálogo de Henry Draper,
así denominado en honor del benefactor que hizo posible está investigación.
La mayoría de las estrellas se conocen por su número en este catálogo, su
HD, por ejemplo HD 155555.
Al principio, los espectros estelares se clasificaron por las intensidades de las
líneas de absorción correspondientes al hidrógeno y a cada tipo o clase
espectral se le denominaba por una letra en orden alfabético : A para las
estrellas con líneas muy intensas de hidrógeno, B para estrellas con líneas
algo más débiles y así sucesivamente. Posteriormente se comprobó que los
tipos de espectros variaban principalmente debido a las diferentes
temperaturas de las atmósferas de las estrellas. Las líneas de hidrógeno son
muy intensas en estrellas que tienen cierta temperatura y sí la temperatura es
más alta o más baja las líneas son más débiles. Se ordenó, entonces, la lista
de tipos espectrales en función de temperaturas decrecientes y naturalmente
ya no quedó en orden alfabético.
Se puede suponer que las estrellas se comportan como cuerpos negros, esta
hipótesis implica que la temperatura y la cantidad luz (flujo: energía por m2 y
segundo) que emite son constantes. Si las estrellas radian como cuerpos
negros se podría deducir su temperatura.
Tipos espectrales
file:///F|/antares/modulo2/m2_u205.html (1 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2-05- Programa de Nuevas tecnologías - MEC -
Se clasifican actualmente las estrellas por sus espectros estelares en una
secuencia espectral caracterizada por una letra que se denomina tipo
espectral o clase espectral, con la temperatura disminuyendo hacia la
derecha.
C
( R - N)
O - B - A - F - G -K - M
S
⇐ Tef
Notaciones adicionales son Q para novas, P para nebulosas planetarias y W
para estrellas Wolf-Rayet. La clase C constituye los antiguos tipos R y N
(estrellas de carbono). Las clase C y S representan ramas paralelas a los tipos
G-M siendo su composición química superficial diferente.
Los tipos O, B, y A se llaman primeros tipos o estrellas tempranas pero no
tiene nada que ver con la edad de las estrellas, también se denominan
estrellas calientes. Las estrellas K, M, N, R, S se llaman estrellas de los
últimos tipos o estrellas frías.
Figura 2-2-6: Espectros
observados para
estrellas de distintas
temperaturas efectivas
(tipos espectrales
diferentes). La más
calientes, arriba,
muestran líneas de
helio y las más frías,
abajo, tienen líneas de
átomos neutros y
moléculas. A
temperaturas
intermedias las líneas
dehidrógeno son más
intensas, en el tipo
espectral A alcanzan su
máxima intensidad.
file:///F|/antares/modulo2/m2_u205.html (2 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2-05- Programa de Nuevas tecnologías - MEC -
Cada uno de estos tipos espectrales se divide, a su vez, en diez subclases
numeradas de 0 a 9. Por ejemplo, en las estrellas de tipo A las más calientes
son las A0, seguidas con menor temperatura por A1, A2, etc., al tipo A9 le
sigue el F0.
Para algunas clases espectrales todavía se puede afinar más, así tenemos la
clase B0.5 que significa entre B0 y B1. Con experiencia es bastante fácil
deducir el tipo espectral por la mera inspección del espectro de una estrella
(Figura 2-2-6).
Las estrellas de tipo O son las más calientes, sus temperaturas son del orden
de 60 000 a 30 000 grados, luego hay suficiente energía par arrancar los
electrones más exteriores de los átomos y el hidrógeno se encuentra casi
todo ionizado, hay poco hidrógeno atómico así sus líneas espectrales son
débiles. Aparecen líneas correspondientes al helio una vez ionizado y a otros
elementos como el silicio y el nitrógeno también ionizados.
Las estrellas de tipo B son algo más frías, de 30 000 a 10 000 grados. Las
líneas de hidrógeno son más intensas que en el tipo anterior y aparecen líneas
de helio neutro.
En el tipo espectral A las temperaturas son del orden de 10 000 a 7 500
grados. Las líneas de hidrógeno alcanzan en esta clase su máxima intensidad
y empiezan a aparecer líneas correspondientes a elementos una vez ionizados
como el magnesio y el calcio. Sirio y Vega son estrellas de esta clase. Los
tipos O, B y A son de color azulado.
Las estrellas de tipo F tienen temperaturas de 7 500 a 6 000 grados. Las líneas
de hidrógeno son más débiles que en la clase A pero las líneas del calcio
ionizado son más intensas. El calcio ionizado una vez tiene dos líneas,
denominadas H y K, que son particularmente intensas y fáciles de reconocer
en el espectro. La estrella polar pertenece a este tipo espectral.
El tipo espectral G es el correspondiente al Sol, las temperaturas son de 6 000
a 5000 grados. Las líneas del hidrógeno son visibles pero las más intensas del
espectro son las líneas H y K del calcio. El color de las estrella de esta clase
es amarillo.
Las estrellas de tipo espectral K son relativamente frías, de 5 000 a 3 500
grados, el espectro está cubierto por muchas líneas que corresponden a
metales no ionizados, en contraste con los espectros de las estrellas calientes
que muestran pocas líneas. Arturo y Aldebaran son de este tipo cuyo color es
rojo.
Las estrellas M son las más frías, con temperaturas inferiores a los 3 500
grados. Sus atmósferas son tan frías que pueden existir moléculas (elemento
constituido por varios átomos, como el agua H2O molécula que tiene tres
átomos dos de hidrógeno y uno de oxígeno) que no se disocian en sus
átomos constituyentes y el espectro muestra muchas líneas moleculares, en
particular son intensas las de la molécula del óxido de titanio. Betelgeuse es
una estrella roja que pertenece a este tipo.
Existen también otros tipos espectrales R, N y S que tienen temperatura
similar al tipo M pero las líneas de sus espectros corresponden a diferentes
átomos y moléculas. Las estrellas de tipo R y N se denominan también de
carbono (C) por presentar una gran abundancia de este elemento. Los
espectros de tipo S se caracterizan por la intensidad de las líneas de la
molécula de óxido de circonio.
file:///F|/antares/modulo2/m2_u205.html (3 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2-05- Programa de Nuevas tecnologías - MEC -
Figura 2-2-7: Tipos
espectrales. Los
espectros observados
se han obtenido con un
CCD, mientras que los
de la Figura 6.5 estan
tomados en placa
fotográfica. Se
representa la
intensidad del espectro
en función de la
longitud de onda, las
líneas de absorción se
ven como una
disminución del
espectro continuo, el
cual tiene una forma
bastante similar a la de
un cuerpo negro a la
temperatura efectiva
de la estrella.
Las diferencias entre los espectros estelares son debidas principalmente a
diferencias de temperatura (Figura 2-2-7) y no de composición química, la
mayoría de las estrellas están constituidas por los mismos elementos y en
aproximadamente la misma proporción.
Así, la composición química obtenida del análisis de los espectros indica que
la mayoría de las estrellas están constituidas principalmente por Hidrógeno
(H) con alrededor de un 10% ± 5% de Helio (He) en número de átomos. Los
elementos más abundantes después son Carbono (C), Nitrógeno (N), Oxigeno
(O), y Neón (NE) que constituyen los cuatro un 1% del número total de
partículas. Los siguientes elementos Silicio (Si), Magnesio (Mg), Hierro (Fe), y
Aluminio (Al) son menos abundantes que C, N, O y Ne en un factor de
aproximadamente 10.
file:///F|/antares/modulo2/m2_u205.html (4 de 4) [12/3/2000 17.09.05]
ANTARES - Módulo 2 - Unidad 2 - 06 - Programa de Nuevas tecnologías - MEC -
Cuestiones y problemas para autoevaluación
●
Cuestiones
●
Problemas
Cuestiones
1. La estrella X tiene un índice de color B-V igual a 0.0 mientras que en la
estrella Y es 1.0 ¿Cuál tiene mayor temperatura efectiva y por qué?
2. ¿Cómo se puede describir el espectro de una estrella de tipo A ?
3. ¿Cómo se puede obtener la velocidad de una estrella respecto al Sol ?
4. Sí una estrella tiene un espectro similar al del Sol, pero todas sus líneas
espectrales están desplazadas un 2% de su longitud de onda hacia el rojo
¿qué podemos decir respecto al movimiento de la estrella?
5. Las diferencias entre los tipos espectrales ¿ a qué son debidas
principalmente?
6. ¿Por qué algunas estrellas tienen intensas líneas de hidrógeno y otras no,
sí se sabe que todas las estrellas contienen aproximadamente el 90% de
hidrógeno?
7. Indicar dos métodos para determinar la temperatura de una estrella.
8. Betelgeuse tiene una temperatura superficial de 3 400K, mientras que Rigel
tiene 10 100 K. ¿En qué región del espectro emiten su máxima radiación?
9. La longitud de onda de laboratorio para la primera línea de la serie de
Balmer de hidrógeno, Hα , es 6562.80 Å. Sin embargo, en el espectro de la
estrella Vega (α Lyrae) la longitud de onda de Hα es 6562.50 Å ¿ Cuál es la
velocidad radial de Vega?
10. El espacio está lleno de la llamada radiación de fondo, resto de la primera
edad del universo. La distribución de esta radiación es similar a la de un
cuerpo negro a la temperatura de 2.7 K. ¿Cuál es la longitud de onda del
máximo de esta radiación?
file:///F|/antares/modulo2/m2_u2autoeva.html (1 de 2) [12/3/2000 17.09.06]
ANTARES - Módulo 2 - Unidad 2 - 06 - Programa de Nuevas tecnologías - MEC -
Problemas
1. Una estrella sufre una explosión de modo que su temperatura efectiva se
duplica pero su densidad disminuye en un factor 8, se supone despreciable
la masa perdida. ¿Cuales serán los nuevos radios y luminosidad de la
estrella?
2. Una estrella tiene Tef = 8700 K, magnitud bolométrica absoluta Mb = 1.6 y
aparente mb = 7.2. Calcular su distancia, luminosidad y radio.
Datos: L¤ = 3.9 x 1026 W ; Mb¤ = 4.77 ; σ = 5.67 x 10-8 W m-2 K-4
file:///F|/antares/modulo2/m2_u2autoeva.html (2 de 2) [12/3/2000 17.09.06]
ANTARES - Módulo 2 - Unidad 2 - 07 - Programa de Nuevas tecnologías - MEC -
Proyectos o actividades de observación
1. Clasificación en tipos espectrales de una muestra de estrellas observadas
desde el Observatorio Astronómico Virtual. Obtención de los espectros,
clasificación y estimación de las temperaturas efectivas. La descripción
completa de esta práctica así como los procesos necesarios para su
realización están explicados con detalle en el Apéndice. Por favor, antes de
acceder al Observatorio, consulte el manual de instrucciones.
file:///F|/antares/modulo2/m2_u2activid.html [12/3/2000 17.09.06]
ANTARES - Módulo 2 - Unidad 2 - 08 - Programa de Nuevas tecnologías - MEC -
Soluciones
●
Cuestiones
●
Problemas
Cuestiones
2. ¿Cómo se puede describir el espectro de una estrella de tipo A ?
Tiene líneas muy intensas de hidrógeno.
5. Las diferencias entre los tipos espectrales ¿a qué son debidas
principalmente?
A la temperatura.
6. ¿Por qué algunas estrellas tienen intensas líneas de hidrógeno y otras no,
sí se sabe que todas las estrellas contienen aproximadamente el 90% de
hidrógeno?
Las condiciones de temperatura y presión no son suficientes
para que puedan observarse.
Problemas
2. Una estrella tiene Tef = 8700 K, magnitud bolométrica absoluta Mb = 1.6 y
aparente mb = 7.2. Calcular su distancia, luminosidad y radio.
Datos: L¤ = 3.9 x 1026 W ; Mb¤ = 4.77 ; σ = 5.67 x 10-8 W m-2 K-4
d = 132 pc
L = 7.21 x 1027 W ;
R = 1.33 x 109 m.
file:///F|/antares/modulo2/m2_u2soluciones.html (1 de 2) [12/3/2000 17.09.06]
ANTARES - Módulo 2 - Unidad 2 - 08 - Programa de Nuevas tecnologías - MEC -
file:///F|/antares/modulo2/m2_u2soluciones.html (2 de 2) [12/3/2000 17.09.06]