Diapositiva 1
Anuncio

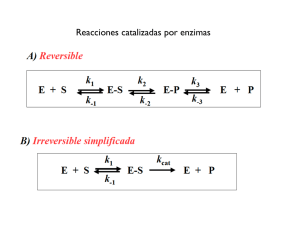
Tema 5 CATÁLISIS ENZIMÁTICA 1. Introducción 2. Teoría del Complejo Activado” o “Teoría del Estado de Transición 3. Perfil Energético de una Reacción Catalizada 4. Perfil energético de una Reacción enzimática Efecto de la concentración de sustrato 5. Centro activos de las enzimas 1. Introducción: La acción catalítica A comienzos del S. XX, Jöns Jacob Berzelius introdujo el término catálisis y llamó catalizadores a aquellas sustancias capaces de aumentar la velocidad de una reacción. Definición Un catalizador es una sustancia que acelera una reacción química pero que no sufre alteración tras el proceso catalítico. Pero esto no supone que el catalizador no intervenga en la reacción química que cataliza. Todo lo contrario, en toda catálisis la molécula de catalizador interacciona directamente con las especies reaccionantes. No modifica la energia libre de Gibbs ∆G Condiciones estándar (∆Go) no modifica la constante equilibrio Ke 2. “Teoría del Complejo Activado” o “Teoría del Estado de Transición” Energía libre de activación de Gibbs k1 S ===== P k-1 G Trabajo máximo útil que, a presión constante, produce o consume un sistema cuando evoluciona de un estado inicial al final P G S ∆G – Reacción exergónica Espontánea ∆G + Reacción endergónica P No espontáneo * Fundamentos básicos: - Para que una reacción tenga lugar, el potencial químico de los reactivos ha de ser mayor que el de los productos. debe haber un desprendimiento de energía libre de Gibbs (∆G < 0). - Para que los reactivos interaccionen entre si, se ha de formar un complejo activado de potencial químico mayor que el de los reactivos en su estado elemental. - La diferencia de energía entre el estado elemental de los reactivos y el del complejo activado es la llamada energía libre de activación de Gibbs, (∆G≠). Esta energía es siempre positiva “representa la energía que debe comunicarse a las moléculas para que pasen del estado elemental al de transición”. S≠ ∆G ∆G≠ S ∆G P - Esta teoría ignora el proceso (mecanismo) por el cual las moléculas reaccionan. Solamente se consideran los estados elementales estables de los reactivos y productos y el estado de transición inestable. - Se supone que todos los estados de transición se descomponen con la misma constante de velocidad a una temperatura determinada. * Esta constante de velocidad está representada por la frecuencia de vibración de los enlaces que se han de romper en el estado de transición * De todo ello deriva el nombre de velocidad absoluta de reacción. Esta constante depende únicamente de la temperatura y es la misma para todas las reacciones químicas. - La frecuencia de vibración de los enlaces a una temperatura determinada es la causante de la ruptura de los enlaces del complejo activado ¿Cómo podemos calcular el valor mínimo de la frecuencia para que se rompa un enlace? La frecuencia de vibración del enlace la podemos obtener igualando: Energía de oscilador excitado (Eν) = Energía potencial del enlace (Ep) Eν = h ν Ep = kBT h ν = kBT k BT h constante Planck ν = k cte Boltzman h ν Frecuencia de vibración B Esta frecuencia de vibración de enlace, ν, representa la constante de velocidad universal a partir de la cual se descomponen/rompen todos los complejos activados. Supongamos una reacción sencilla monomolecular, una isomerización por ejemplo: S P - Según la “Teoría del estado de transición”: S S# P S# dará lugar a P al descomponerse según la “constante de velocidad universal”, ν, a una temperatura determinada. Vreacción − d[S] # = =ν S dt [ ] Por otro lado, según la Cinética, Vreacción = k [ S] Igualando ambas ecuaciones: [ ] k [ S] = ν S # [ ] ν S k= [S] # Teniendo en cuenta que el S y el S# están en equilibrio, podemos definir una constante de equilibrio de formación del complejo activado, [ ] ν S k= [S] # K = # [S ] # [S] k BT # k = νK = K h # k = νK # k BT ν = h - Si expresamos la cte de equilibrio de activación, K#, en function de la energía libre de Gibbs de activación: # ∆ G = − RTLnK # # k BT k= e h K# = e − ∆ G# RT −∆G RT k valor de la constante de velocidad o constante cinética de la reacción S P - Y teniendo en cuenta que: ∆G# = ∆H# - T∆S# k BT k= e h − ∆H RT # e ∆S R # Expresión que se conoce como ecuación de Eyring, que expresa el valor de la constante de velocidad en función del incremento de la entalpía de activación y de la entropía de activación. * Una propiedad característica de los catalizadores es que catalizan igualmente la reacción en sentido directo como la reacción en sentido inverso, es decir no influyen sobre la constante de equilibrio. k1 S ===== P k-1 k1 k-1 ∆G # k1 keq = k−1 3. Perfil Energético de una Reacción Catalizada Reacción sin catalizar S ≠ Reacción catalizada ∆G≠nc SC≠ ∆G≠c S ∆G P Existen diferentes clases de catalizadores químicos - Catalizadores homogéneos: La reacción catalizada se produce por completo en una fase. Ventaja de difusión de moléculas reactantes y catalizador Ej. OH- Hidrólisis de ester (saponificación de trigliceridos) - Catalizadores heterogéneos: la reacción catalizada se produce en una superficie entre dos fases. Catalizador Sólidos. Proceso adsorción Sustrato sobre zonas Centro activos Ventaja Especificidad * Todas las reacciones catalizadas parecen transcurrir a través de la formación de una “especie intermedia” formada entre el catalizador y el sustrato. Catálisis enzimática -Enzimas solubles Solución. Fluidos biológicos, citosol celular, lisosomas,vacuolas, estroma del cloroplasto, et -Enzimas particuladas. Membranas plasmáticas , mitocondriales o otros orgánulos celulares. Peso Molecular 30-50 Kda Metabolitos 0.2-0.4 Kda Catálisis microheterogénea Ventajas de la homogénea y heterogénea Facilita la difusión HIDROLASAS ?? Alta especificidad 4. Perfil Energético de una Reacción Enzimática Reacción sin catalizar S‡ Reacción catalizada ∆G‡nc SC ‡ ∆G‡c S ∆G P * Hemos representado el perfil energético o coordenadas de reacción para una reacción catalizada y no-catalizada en general, teniendo, únicamente, en cuenta los estados inicial y final y el estado de transición del S de acuerdo con la “Teoría del Estado de Transición” * Sin embargo, en el caso de una reacción catalizada por una enzima hemos de tener en cuenta la formación del complejo-ES (o de los complejos enzima-sustratos, si la reacción tiene más de un sustrato), que es el que pasa al Estado de Transición, ES‡, o complejo activo, -en una reacción que es siempre monomolecular-. Supongamos la siguiente reacción elemental: S <=====> P Catalizada por la enzima, E. - Para esta reacción enzimática podemos considerar los siguientes pasos: E + S <==> ES* <==> ES <==> ES# <==> EP <==> EP* <==> E + P Estado de Transición para la formación del complejo-ES Estado de Transición de la reacción global Estado de Transición para la formación del complejo-EP ES# ES* E+S ES EP* EP E+P ES# ES* E+S ES EP* EP E+P De acuerdo con la anterior secuencia de reacciones, podemos definir una serie de energías libres de Gibbs: ∆G --> Energía libre actual de la reacción S<===>P en el supuesto de una reacción espontánea en la dirección S-->P, ∆G será negativo ES# ES* E+S ES ∆G EP* EP E+P ∆Gs* --> Energía libre de activación para la formación del complejo-ES* a partir de E libre y del S inicial. Esta energía será siempre positiva ES# ES* E+S ∆Gs* ES EP* EP E+P ∆Gp* --> Energía libre de activación para la formación del complejo-EP* a partir de E libre y de P. Esta energía será siempre positiva ES# ES* E+S ES EP* ∆Gp* EP E+P ∆Gs --> Energía libre actual para la formación del ES a partir de E libre y de S. ES# ES* E+S ∆Gs ES EP* EP E+P ∆GT# --> Energía libre de Gibbs para la formación del complejo-ES activado, ES#, a partir de la enzima, E, y del sustrato, S. ES# ∆GT# ES* E+S ES EP* EP E+P ∆G# Energía libre de Gibbs para la formación del complejo-ES activado, ES#, a partir del complejo-ES, (su valor es siempre positivo), y equivale a la energía de activación. ES# ∆G # ES* E+S ES EP* EP E+P * El valor de ∆G# marca la velocidad de reacción ecuación de Eyring Constante cinética de velocidad de una reacción catalizada por una enzima k BT k= e h − ∆ H# RT e ∆ S# R Valores de la entropia y entalpia de activación a una temperatura determinada ΔH# Entalpia de transición es siempre positivo indica la energía que debe entregarse a los reactantes para alcanzar el estado de transición ΔS# Entropia de transición deberá aumentarse para catalizar la reacción EFECTO DE LA CONCENTRACIÓN DE SUSTRATO SOBRE ∆G# ∆Gs = ∆G 0 S [ ES ] + RT ln [E ][S ] Ks constante de disociación de la formación de complejo ES a partir de E y S ∆GS0 = RT ln Ks ∆Gs = Signo dependerá Ks [S ] ∆Gs = [ ES ] RT ln Ks + RT ln [E ][S ] [ Ks ES ] + RT ln RT ln [S ] [E ] ES ES>>E Substrato está en exceso [E ] >1 [S] > Ks [S ] valor de ∆Gs Ks ES* E+S ES ∆Gs [S] < ES* Ks E+S ∆Gs Perfiles energéticos a diferentes valores de la razón Ks/S ES‡ ∆G E+S ES S>Ks ES‡ ∆GT# ES ∆G E+S ∆Gs ∆GT# ∆Gs S<Ks Una enzima el poder catalítico es mayor a pequeñas concentraciones de sustrato Afinidad por el sustrato es elevada y la concentracion es alta, el complejo ES cae en un pozo de potencial 5. CENTRO ACTIVO DE LAS ENZIMAS Región de la enzima donde se une el sustrato (o sustratos) NOTA: Este centro activo es, con frecuencia, un bolsillo o cavidad rodeada por cadenas aminoacídicas laterales que facilitan la unión del sustrato y por otras que participan en la catálisis. La estructura terciaria de las enzimas hace posible que en este bolsillo se ajuste el sustrato de manera muy estrecha, lo cual explica la extraordinaria especificidad de la catálisis enzimática. 129 aminoácidos Centro activo 35,52,62,63 y 101 Catálisis Glutámico 35 Aspartico 52 Enlaces no covalentes: Electrostáticos, puentes de hidrógeno, fuerzas de Van der Waals, interacciones hidrofóbicas. . Esto es debido a la flexibilidad de la enzima para acoplarse o ajustarse al sustrato *Emil Fischer (1894) hipótesis de la “cerradura y la llave” (lock and key) Selectividad: complementaridad adaptabilidad Elementos: geometría, H, carga, puentes de etc. Supone una rigidez en ambas estructuras no compatible con la realidad de las moléculas de los sustratos y enzimas en solución - Este modelo explicaba la especificidad enzimática, pero no permitía entender la catálisis en sí, ya que una cerradura no hace nada a su llave. - El propio Fischer dio el primer paso para entender mejor la catálisis, “.. lo que se ajusta mejor al centro activo de la enzima es una molécula de sustrato a la que se induce a adoptar una configuración que se aproxima al estado de transición”. - En otras palabras, la enzima no acepta simplemente al sustrato, sino que también le obliga a que se distorsione, tomando la forma de algo cercano al estado de transición. En 1958 Daniel Koshland elabora y madura esta idea y propone la hipótesis del “Ajuste Inducido” (induced fit), que actualmente continua siendo el modelo más aceptado. El “ajuste inducido” implica tanto la distorsión del sustrato como de la enzima, pudiendo ser esta distorsión local o comportar un cambio importante de la conformación molecular de la enzima (ver p. ej. caso de la hexoquinasa). RESUMEN 1. Catálisis enzimática se considera como catálisis micro-heterogénea. Ventajas de difusión facilitada y especificidad del centro activo 2. Teorías de las velocidades absolutas de reacción. Todas las substancias para reaccionar deben pasar a un estado activado. La constante de velocidad de ruptura de enlace en el estado activado es igual a la frecuencia de vibración de los enlaces de los enlaces en el estado de activación. Se define una energía libre de activación de Gibbs ∆G# o energía necesaria para alcanzar el estado activado. 3- Enzimas Rebajan la ∆G# . Formacion del complejo ES # a partir del complejo ES. La formación del complejo hay perdida de Entropia que es compensada por el calor de reacción ∆Hs. El signo de energía libre de formación del complejo ES depende de la relación Ks/S 4-Centro activo un bolsillo o cavidad rodeada por cadenas aminoacídicas laterales que facilitan la unión del sustrato y por otras que participan en la catálisis Hipótesis del “ajuste inducido”. Los sustratos producen un ajuste inducido (cambio conformacional) del centro activo.