FÍSICA EXPERIMENTAL I TRABAJO PRACTICO DE
Anuncio

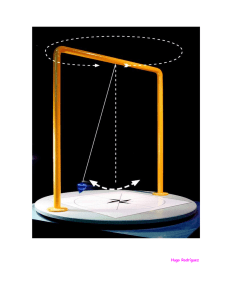
FÍSICA EXPERIMENTAL I TRABAJO PRACTICO DE LABORATORIO Nº 2 Péndulo Objetivo Específico: Determinación de la aceleración de la gravedad local con una incertidumbre porcentual del orden de 0,1%. Objetivo General: - Familiarizarse con la medición de tiempos. - Tratamiento de incertidumbres Tipo A. - Propagación de incertidumbres. - Construcción de histogramas Introducción: Consideremos el péndulo que se muestra en la Fig. 1, formado por un cilindro de masa mC, radio r y longitud Lc, suspendido de un hilo inextensible de radio despreciable, masa mH y longitud LH. El hilo esta sostenido por un prisma rectangular de masa mP, de lados a y b que pivotea alrededor de dos puntos de apoyo, como se muestra en la Fig. 1. b a LH L=LH+LC/2 θ0 Figura 1. Esquema del péndulo a utilizar para medir la aceleración de la gravedad local. Las cantidades están definidas en el texto. (a): Vista de frente. (b): Vista lateral. Llamemos I al momento de inercia de un péndulo respecto a su eje de rotación, M a su masa total, d a la distancia entre el punto de suspensión y el centro de masa del péndulo y g a la aceleración de la gravedad local. Si θ0 es la amplitud angular de oscilación, el período de oscilación del péndulo, despreciando efectos de fricción, se describe por la expresión: T = 2π I Mgd k 2 9 k 4 25 k 6 1 + 2 + + + .......... 2 2 44 4 8 2 k = sen θ0 2 En el límite de pequeñas amplitudes de oscilación (θ0 « 1) el período se puede aproximar de la siguiente manera: T = 2π I Mgd θ o2 1 + 16 Para el péndulo de la Fig. 1, escribiendo adecuadamente I, M y d en términos de las cantidades a medir directamente (masas y distancias), se llega a la siguiente expresión: 2 2 L m L2 m 2 1 + 1 C2 + 1 mC r 2 + 1 H H2 + 5 P a 2 4 12 mC L L 3 mC L L 12 L T = 2π g 1 m H LH 1 m P a 1 + + 2 mC L 2 mC L θ 02 1 + 16 Esta expresión se puede utilizar para medir g en término de las restantes cantidades, conservando solo términos cuadráticos de θ0: g = 4π 2 L T2 2 2 L m L2 m 2 1 + 1 C + 1 r + 1 H H + 5 P a 12 L2 4 L2 3 mC L2 12 mC L2 θ 02 1 + 8 1 m H LH 1 m P a 1 + + 2 mC L 2 mC L (1) Si asumimos que mH « mC , mp « mC , LC « L, r « L, a « L y b « L y recordando que L=LH+LC/2, obtenemos para g en un desarrollo hasta segundo orden: g ≈ 4π 2 L T2 2 2 θ 2 m L m m2 m L 1 + 1 C + 1 r − 1 H + 1 H − 1 H C − 1 p a 1 + 0 12 L 2 4 L 2 6 m 12 mC2 12 mC L H 2 mC L H 8 C H H Conservando solo términos de primer orden la expresión anterior se reduce a: g ≈ 4π 2 L T2 1 mH 1 − 6 mC θ 02 1 + 8 (2) A modo de ejemplo se ha graficado, en la Fig. 2, la diferencia relativa entre la ecuación (1) y la ecuación (2) en función de la longitud del hilo, para un péndulo compuesto por: un cilindro de 700 g de masa, 5 cm de largo y 4 cm de diámetro, un hilo con densidad lineal λH=1 g/m y un prisma rectangular de lados a = 1 cm, b =5 cm y 67 g de masa. -5 5.0x10 Diferencia relativa 0.0 -5 -5.0x10 -4 -1.0x10 -4 -1.5x10 -4 -2.0x10 0.8 1.2 1.6 2.0 2.4 2.8 LH [m] Figura 2. Diferencia relativa entre la ecuación (1) y la ecuación (2) en función del largo del hilo. Despreciando el término de primer orden (mH/6mC) y el de segundo orden en la amplitud en la ecuación (2), esta se reduce a la correspondiente a un péndulo simple: g = 4π 2 L T2 (3) A partir de las expresiones (1), (2) o (3) (o de alguna otra expresión apropiada) se puede determinar, con distinto grado de aproximación, la aceleración de la gravedad g midiendo las distintas cantidades que intervienen en ellas. Procedimiento: Parte I: Medición preliminar de g. A modo de entrenamiento mida T y L en no más de 5 minutos y determine el valor de g, con su incertidumbre, haciendo uso de la ecuación (3). Parte II: Introducción al análisis de incertidumbres tipo A. Utilizando un cronómetro mida 100 veces el tiempo correspondiente a 10 períodos del péndulo. Construya un histograma con los valores medidos. Calcule el valor medio y la desviación estándar de las mediciones. Investigue la dependencia de la desviación estándar con la cantidad de mediciones. Para ello calcule la desviación estándar de las n primeras mediciones (n=5, 10, 15,..100). Grafique la desviación estándar en función de n. Parte III: Planee el experimento para medir g con una incertidumbre porcentual del orden de 0,1%. Decida qué expresión utilizará para obtener el valor de g en función del experimento que llevará a cabo. Evalúe el efecto del amortiguamiento en el período del péndulo. Parte IV: Determine el valor de g con su respectivo error, utilizando un fotodetector y una central de adquisición de datos para medir el período del péndulo. Determine el valor de g con su respectivo error. APENDICE A Uso de la calculadora (Fuego, Casio y semejantes) Encienda la calculadora con la tecla ON Apriete la tecla MODE Aparecerá en la pantalla COMP 1 SD 2 REG 3 COMP (computar) uso corriente SD (estadística) REG (regresión o cuadrados mínimos) Apriete la tecla 2 Aparecerá en parte superior de la pantalla en letras muy pequeñas SD En este modo de cálculo su calculadora le permite ingresar un conjunto de n datos, calcular su valor medio y dispersión cuadrática media de un modo muy simple. Para ello Teclee el primer valor de sus n datos y luego Apriete la tecla M+ Así habrá ingresado su primer valor. Repita la operación todas las veces que haga falta. Si n=40 tendrá que apretar 40 veces la teclas M+ posterior a cada dato que haya tecleado. Algunas calculadoras con mucha memoria permiten recorrer la tabla de datos que se ingresa mediante el uso de las flechas. Esto permite revisar los datos ingresados. En la mayoría de las calculadoras esto no se puede hacer por lo que deberá tener cuidado en el ingreso de datos. Apriete la tecla SHIFT y luego la tecla 1 para obtener el número n de datos ingresados. Le aparecerán 3 opciones Apriete la que corresponda y luego Apriete = Apriete AC (función de pantalla clear all) SHIFT y 2 para obtener el valor del x medio o el valor de la dispersión cuadrática media (calculada usando n o n-1 según necesite). Apriete la tecla luego la tecla Antes de ingresar sus datos asegurarse que la memoria esté en cero.