A n

ÁLGEBRA:
MATEMÁTICA DISCRETA
Parte 1ª: Combinatoria y Recurrencia
Profesor: José-Miguel Pacheco Castelao
Curso 2011-2012
ESCUELA DE INGENIERÍA INFORMÁTICA DE LA ULPGC
1
Combinatoria Elemental (1)
La Combinatoria es la parte de las Matemáticas cuyo objetivo es establecer modos y
fórmulas para contar diversas clases de objetos y grupos de ellos, seleccionados de entre
un conjunto finito. Partimos, pues, de un conjunto A formado por n elementos, todos ellos
diferentes.
Una primera pregunta combinatoria es: ¿De cuántas maneras pueden elegirse k
elementos distintos entre los n disponibles?
Para empezar, supondremos que k<n , y como ejemplo, pongamos k=2. Podemos
seleccionar un primer elemento de A de n maneras, pues A tiene n elementos. Una vez
elegido éste, como el segundo ha de ser diferente de él, quedarán n-1 posibilidades para él.
Por tanto el número posible de parejas será n(n-1), como puede verse construyendo una
tabla de doble entrada.
Hemos utilizado, sin definirlo, el llamado principio fundamental de la Combinatoria:
Si un objeto a se puede elegir de p modos y otro b de q maneras, el número
posible de pares (a,b) es pq.
2
Elemento nº
1
2
3
…
k-1
k
Posibilidades:
n
n-1
n-2
…
(n-k+2)
(n-k+1)
Nº objetos
por grupo
1
2
3
…
k-1
k
Nº de
grupos
n
n(n-1)
n(n-1)(n-2)
…
n(n-1)…(n-k+2)
n(n-1)…(n-k+1)
Construcción y recuento de las Variaciones sin elementos repetidos
Una Variación es un grupo formado por k elementos distintos, seleccionados entre los n
disponibles. Dos variaciones de k elementos se diferencian entre sí, bien por los objetos que
las componen, bien por el orden en que aparecen los componentes. El número de
variaciones se obtiene a partir de la tabla y resulta ser:
Vkn = n(n − 1)(n − 2)...(n − (k − 1)) =
= n(n − 1)(n − 2)...(n − k + 1)
3
Elemento nº
1
2
3
…
k-1
k
Posibles:
n
n
n
…
n
n
Nº objetos
por grupo
1
2
3
…
k-1
k
Nº de
grupos
n
nxn
nxnxn
…
nxnx…xn
(k-1 veces)
nxnx…xn
(k veces)
Construcción y recuento de las Variaciones si se permite que los elementos se repitan
En este caso la tabla se modifica según se ve más arriba, pues una vez elegido un objeto,
éste se devuelve al conjunto A y puede volver a ser seleccionado. Ahora se puede trabajar
también con k>n. Los grupos así formados se llamarán variaciones con repetición, y su
número será:
VRkn = n × n × n.... × n = n k
4
Construcción y recuento de las Variaciones sin repetición cuando n=k.
De acuerdo con la definición de las Variaciones sin repetición, cuando n=k dos variaciones
sólo se diferencian en el orden de aparición de sus elementos. Los grupos así formados se
llamarán Permutaciones de los n elementos, y su número será:
Vnn = n × (n − 1) × (n − 2).... × 2 × 1 = n !
n
n!
0
1
1
1
2
2
3
6
4
24
5
120
6
720
7
5040
8
40320
…
…
o bien, cambiando la notación,
Vnn = Pn = n !
La expresión n! se lee factorial de n.
Las factoriales crecen con gran rapidez,
según se ve en la tabla adjunta.
Es necesario definir la factorial de 0
como 1 para que los desarrollos
posteriores tengan sentido…
5
Construcción y recuento de las Combinaciones (sin repetición)
Una combinación es simplemente un grupo de k elementos distintos seleccionados entre los
n disponibles. Dos combinaciones de k elementos se diferencian entre sí sólo por los objetos
que las componen, pero no por el orden en que aparecen. Dada una combinación cualquiera
de k elementos, habrá k! variaciones con esos mismos elementos, porque las posibles
permutaciones –que no cambian la combinación– son k!, luego el número de combinaciones
es:
n
V
n(n − 1)(n − 2)...(n − k + 1)
Ckn = k =
=
Pk
k!
[n(n − 1)(n − 2)...(n − k + 1)] × (n − k )!
=
=
k !× (n − k )!
n!
=
k !(n − k )!
6
Notaciones, definiciones, y la ley de simetría
El número de las combinaciones se suele escribir abreviadamente así:
⎛n⎞
n!
C =
=⎜ ⎟
k !(n − k )! ⎝ k ⎠
n
k
Estos números se llaman números combinatorios o coeficientes binómicos, y se
leen: n sobre k.
De la construcción de los números combinatorios se deduce inmediatamente la
siguiente Ley de Simetría, que permite ahorrar la mitad de los cálculos:
⎛n⎞ ⎛ n ⎞
n!
n!
n
=⎜ ⎟=⎜
=
=
C =
C
n−k
⎟
k !(n − k )! ⎝ k ⎠ ⎝ n − k ⎠ (n − k )!k !
n
k
7
Algunas observaciones sobre números combinatorios
Si hacemos k=0, la fórmula de las combinaciones será
n! ⎛ n ⎞
C =
= ⎜ ⎟ =1
0!n ! ⎝ 0 ⎠
n
0
Véase que hemos necesitado usar la convención sobre la factorial de 0, esto es,
0!=1. Sin ella sería imposible calcular el cociente que define el número
combinatorio.
Dicho de otra manera, cuando k=0 estamos construyendo grupos con cero
elementos: Sólo hay un modo de conseguirlo, que es… ¡no elegir nada!
8
Leyes de Recurrencia (1)
Al construir las factoriales se puede observar que la factorial de un número se obtiene
multiplicando dicho número por la del número anterior. En efecto:
n ! = n × (n − 1) × (n − 2)... × 2 × 1 =
= n × [ n − 1) × (n − 2)... × 2 × 1] =
= n × [(n − 1)!]
Este es un caso de Ley de Recurrencia. Vamos a definir estas Leyes de modo más preciso:
Supongamos que para cada número entero n existe una fórmula que denominaremos F(n).
Dicha familia de fórmulas se llama recurrente cuando es posible obtener la n-sima fórmula
a partir de un número fijo de las anteriores mediante una regla (la ley de recurrencia),
siempre la misma, realizable mediante un número finito de operaciones. En los casos más
simples, la recurrencia se plantea entre la fórmula n-sima y su inmediata anterior
F (n) = R[ F (n − 1), F (n − 2),..., F (n − r )]
Caso más simple: F (n) = R[ F (n − 1)]
9
Por ejemplo, el caso de las factoriales se puede enmarcar en esta teoría en la forma
F (n) = n ! = n × (n − 1)! = n × F (n − 1) = R[ F (n − 1)]
Vemos que podemos ir descendiendo desde F(n) hasta la última posible, que sería F(1) ó
F(0), según qué problema estemos manejando. Estos valores iniciales son los únicos
necesarios para calcular todos los demás. Por tanto, una ley de recurrencia necesita
especificar la regla de formación y los datos iniciales:
F (n) = R[ F (n − 1)]
F (1) = F1 (ó F (0) = F0 )
Por ejemplo, el conjunto de todas las factoriales de los números naturales constituye la
solución del problema de recurrencia
F (n) = nF (n − 1)
F (0) = 1
10
La Ley de Recurrencia básica de la Combinatoria
En las Matemáticas Discretas, y en particular en la Combinatoria, hay gran abundancia de
leyes recurrentes. La mayor parte de ellas usan recurrencia sobre más de una variable.
Vamos a ilustrarlo con el caso conocido como Triángulo Combinatorio o Triángulo de
Pascal:
⎛ n + 1⎞ ⎛ n ⎞ ⎛ n ⎞
⎜
⎟ = ⎜ ⎟+⎜
⎟
k
1
k
k
1
+
+
⎝
⎠ ⎝ ⎠ ⎝
⎠
Esta fórmula es un caso particular de una ley de doble recurrencia del tipo:
F ( n + 1, k + 1) = R [ F ( n , k ), F ( n , k + 1)]
En estos casos, las condiciones suplementarias consisten en especificar los valores:
F (0, k ) = F0 k , F ( n , 0) = Fn 0 , F (0, 0) = F00
A continuación construiremos una tabla para describir esta recurrencia.
11
⎛ n + 1⎞ ⎛ n ⎞ ⎛ n ⎞
⎜
⎟ = ⎜ ⎟+⎜
⎟
k
1
k
k
1
+
+
⎝
⎠ ⎝ ⎠ ⎝
⎠
El Triángulo Combinatorio
k
0
1
0
1
dato
inicial
1
1
1
2
1
2
1
3
4
5
1
1
1
3
4
5
3
6
10
1
4
10
1
5
1
6
7
8
1
1
1
6
7
8
15
21
28
20
35
56
15
35
70
6
21
56
n
2
3
4
5
éste
más éste
6
…
1
7
28
1
8
dan éste
12
Algo sobre el triángulo de Pascal: Justificación del nombre de “coeficientes
binómicos” para los números combinatorios
⎛n⎞
n
Triángulo de Pascal, ⎜ ⎟
⎝k ⎠
nk
0
1
2
3
4
5
6 …
0
1
1
1
1
2
1
2
1
3
1
3
3
1
4
1
4
6
4
1
5
1
5
10 10
5
1
6
1
6
15 20 15
6
1
7
1
7
21 35 35 21
7
8
1
8
28 56 70 56 28 …
0
1
1
1
1
2
1
2
1
3
1
3
3
1
4
1
4
6
4
5
…
…
…
…
6
7
1
8
1
…
…
…
…
Coeficientes del desarrollo de las
sucesivas potencias de (a + b) n
13
Conjetura sobre los coeficientes del desarrollo de las potencias de un binomio.
Observando detenidamente los cuadros anteriores resulta razonable preguntarse si los
coeficientes del desarrollo de las potencias del binomio a+b coincidirán siempre con los
correspondientes números combinatorios cuyo elemento superior es igual a la potencia
con que se trabaje. En otras palabras, se intuye o conjetura que:
⎛ n ⎞ n−k k
n
=
+
a
b
a
b
(
)
∑
⎜ ⎟
k =0 ⎝ k ⎠
n
Para asegurar que la conjetura es cierta –con lo que ya se transforma en un Teorema–
necesitamos una Demostración por Inducción.
La inducción es el proceso mental por el cual se obtiene conocimiento general a
partir del conocimiento de casos particulares.
En Matemáticas la inducción se plantea en la siguiente forma: Si se tiene una familia de
fórmulas f(n), para n=0,1,2,3…, de las que se sabe que son válidas las primeras ¿cómo
podemos asegurarnos de que todas son válidas? Las primeras fórmulas son los casos
particulares, y el núcleo del proceso de demostración consiste en establecer con claridad
que se puede pasar de la fórmula f(n) a la siguiente f(n+1).
14
Demostración por Inducción y sus tres pasos.
Este tipo de demostración nos dice que la fórmula f(n) es válida para todos los valores de n
si se cumple que:
• Se puede comprobar que los primeros casos de la fórmula f(n) son válidos, y que
• tras suponer que hasta un cierto valor de n es cierto lo que se afirma,
• es posible construir la fórmula f(n+1) a partir de la f(n).
Veámoslo para los coeficientes binómicos:
⎛ n ⎞ n−k k
Sea cierto que hasta el número n es f (n) = (a + b) = ∑ ⎜ ⎟ a b
k =0 ⎝ k ⎠
Poniendo (a + b) n +1 = (a + b)(a + b) n =
n
n
n
⎛ n ⎞ n−k k
⎛ n ⎞ n − k +1 k n ⎛ n ⎞ n − k k +1
= ( a + b)∑ ⎜ ⎟ a b = ∑ ⎜ ⎟ a
b + ∑⎜ ⎟ a b =
k =0 ⎝ k ⎠
k =0 ⎝ k ⎠
k =0 ⎝ k ⎠
n +1 n + 1
⎛
⎞ ( n +1) − k k
= ∑⎜
b = (a + b) n +1 = f (n + 1)
⎟a
k =0 ⎝ k ⎠
n
El paso intermedio, marcado en rojo, se obtiene aplicando la recurrencia del triángulo de
Pascal (pista: desarrollar los sumatorios y reordenar los términos)
15
Una consecuencia (Suma por filas en el triángulo de Pascal), y un vistazo a la Teoría de
Conjuntos:
Pongamos a = b = 1 en la fórmula del binomio, con lo que tendremos que la suma de los
números de la n-sima fila del triángulo de Pascal es:
⎛ n ⎞ n−k k n ⎛ n ⎞ n
(1 + 1) = ∑ ⎜ ⎟1 1 =∑ ⎜ ⎟ = 2 , o bien
k =0 ⎝ k ⎠
k =0 ⎝ k ⎠
⎛n⎞ ⎛n⎞
⎛n⎞
n
2 = ⎜ ⎟ + ⎜ ⎟ + ... + ⎜ ⎟
⎝0⎠ ⎝1⎠
⎝n⎠
n
n
Análogamente, si ponemos a =1 y b= -1, se tiene que:
n
⎛ n ⎞ n−k
⎛n⎞
k
0 = (1 − 1) = (1 + (−1)) = ∑ ⎜ ⎟1 (−1) =∑ (−1) k ⎜ ⎟, o bien
k =0 ⎝ k ⎠
k =0
⎝k⎠
n
⎛n⎞ ⎛n⎞ ⎛n⎞
⎛ n ⎞
n⎛ ⎞
+
−
0 = ⎜ ⎟ − ⎜ ⎟ + ⎜ ⎟ − ... + (−1) n −1 ⎜
(
1)
⎟
⎜ ⎟
⎝ 0⎠ ⎝ 1⎠ ⎝ 2⎠
⎝ n − 1⎠
⎝ n⎠
n
n
n
16
La fórmulas anteriores tienen algunas consecuencias interesantes. Notemos que el número
combinatorio “n sobre k” representa el número de posibles subconjuntos del conjunto
original A que tienen k elementos. Por tanto, el número total de subconjuntos se puede
calcular observando el desarrollo del binomio con a = b = 1.
El número n de elementos de un conjunto finito A se llama "cardinal de A",
y se escribe A = n.
La familia de todos los subconjuntos de A es otro conjunto que se llama
"Partes de A", y denotamos P ( A). La fórmula anterior se puede escribir ahora:
P( A) = 2 = 2n
A
Dado que cada elemento de A es por sí solo un subconjunto de A, hemos probado también que para conjuntos finitos, P ( A) = 2 > A , o sea, que 2n > n.
A
17
Trabajando con el triángulo de Pascal: Sumar por columnas…
nk
0
1
2
3
4
5
6 …
0
1
1
1
1
2
1
2
1
3
1
3
3
1
4
1
4
6
4
1
5
1
5
10
10
5
1
6
1
6
15
20
15
6
1
7
1
7
21
35
35
21
7
1
8
1
8
28
56
70
56
28
…
La suma de los n primeros números,
incluidos los ceros del principio, de
la columna k-ésima viene dada por la
fórmula siguiente, que se demuestra
por inducción sobre n:
⎛ m ⎞ ⎛ n + 1⎞
∑
⎜ ⎟ =⎜
⎟
m=0 ⎝ k ⎠
⎝ k + 1⎠
n
18
Trabajando con el triángulo de Pascal: Sumar por diagonales…
nk
0
1
2
3
4
5
6 …
0
1
1
1
1
2
1
2
1
3
1
3
3
1
4
1
4
6
4
1
5
1
5
10
10
5
1
6
1
6
15
20
15
6
1
7
1
7
21
35
35
21
7
1
8
1
8
28
56
70
56
28
…
La suma de los n primeros números,
de la diagonal m-ésima viene dada
por la fórmula siguiente, que se
demuestra por inducción sobre n:
⎛ m + k ⎞ ⎛ m + n + 1⎞
∑
⎜
⎟ =⎜
⎟
k
n
k =0 ⎝
⎠ ⎝
⎠
n
19
Combinatoria Elemental (2)
Combinaciones con repetición y la técnica de RENOMBRAR los elementos…
Ejemplo ilustrativo para el cálculo del número de Combinaciones con elementos repetidos.
Consideremos un conjunto A = {1,2,3,4,5} con 5 elementos, y vamos a construir
ordenadamente todas las posibles combinaciones de 3 elementos, permitiendo que haya
repeticiones. Para ello formamos la tabla de la izquierda, obteniendo 25 de ellas. Añadiendo
las 10 combinaciones ordinarias, aparece el total de 35 posibilidades existentes
111 222 333 444 555
112 223 334 445
113 224 335 455
114 225 344
115 233 355
122 244
133 255
144
155
En general, podemos renumerar los
elementos de A según la siguiente regla:
123 234 345 456 567
El elemento i-ésimo seguirá llamándose i si
está en primera posición. En caso contrario,
se llamará i+j-1, siendo j el puesto que ocupa
en la combinación.
124 235 346 457
En el ejemplo, el mayor valor posible para
i+j-1 es 5+3-1=7, luego…
127 245 357
vemos que las combinaciones con
repetición de 5 objetos tomados de 3 en 3
son las mismas que las de 7 (=5+3-1) sin
repetición tomados de 3 en 3 (tabla de la
derecha)
125 236 347 467
126 237 356
134 246
145 247
156
167
20
En general, para n objetos y grupos de k, el número de Combinaciones con
elementos repetidos vendrá dado por la fórmula:
⎛ n + k − 1⎞
n + k −1
CR = ⎜
⎟ = Ck
⎝ k ⎠
En particular, volviendo al ejemplo motivador:
n
k
⎛ 5 + 3 − 1⎞
⎛7⎞
5 + 3−1
= ⎜ ⎟ = 35
CR = ⎜
⎟ = C3
⎝ 3 ⎠
⎝ 3⎠
5
3
Nótese que en el cálculo del número de las Combinaciones con repetición puede
ocurrir que k > n, como en las Variaciones con repetición.
21
Permutaciones con elementos repetidos
Ejemplo ilustrativo del cálculo del número de Permutaciones con elementos repetidos
Supongamos dadas las permutaciones de tres elementos, p. ej. {a,b,c}, que son 3! = 6.
Permitamos que uno de ellos se repita, digamos que el primero, dos veces: (a,a,b,c). Ahora
tendremos 4 elementos, y 24 permutaciones posibles. Si numeramos las dos a’es como a1 y a2,
observamos que las 24 permutaciones son todas diferentes, pero si les quitamos los índices,
dos permutaciones como (a1,b,c,a2) y (a2,b,c,a1) se convierten en indistinguibles, pues ambas
se escriben igual, (a,b,c,a). Esto es, cada dos permutaciones con las dos a’es intercambiadas se
convierten en una sola. Como en todas las permutaciones hay dos a’es, nos quedará que sólo
son posibles 24/2 = 24/2! = 12 permutaciones distintas de 4 elementos, siendo dos de ellos
iguales.
En general, siguiendo este mismo razonamiento obtendremos:
Pnn1 ,n2 ,...,nr =
n!
n1 !n2 !...nr !
Nótese que se ha de cumplir que n = n1 + n2 + ... + nr
22
Una observación sobre el número de permutaciones con elementos repetidos.
Consideremos en la fórmula de la permutaciones con repetición que r = 2. En tal caso
se tiene que:
n
n1 , n2
P
⎛n⎞ ⎛ n⎞
n!
n!
n!
n
, y como n = n1 + n2 , Pn1 ,n2 =
=
=
= ⎜ ⎟ = ⎜ ⎟.
n1 !n2 !
n1 !n2 ! n1 !(n − n1 )! ⎝ n1 ⎠ ⎝ n2 ⎠
⎛n⎞
Si ponemos n2 = k , observamos que Ckn = ⎜ ⎟ = Pnn− k ,k . Esto permite reescribir
⎝k ⎠
la fórmula del binomio en una forma más simétrica:
( a + b) n =
∑
k = 0,..., n
Pnn− k ,k a n − k b k
La importancia de esta nueva forma es que pone de relieve el hecho que la
construcción de la fórmula del binomio se reduce a saber de cuántas maneras se
puede descomponer el número n en suma de otros dos, teniendo en cuenta el
orden de los sumandos. Además esto abre la vía a una generalización natural,
cambiando binomio por trinomio, cuatrinomio, polinomio,…
23
Un ejemplo ilustrativo: La potencia n-sima de un trinomio.
(a + b + c) n =
∑
n1 + n2 + n3 = n
Pnn1 ,n2 ,n3 a n1 b n2 c n3
Todos los términos del sumatorio son de grado n, como muestra el hecho de que los exponentes
suman n. A cada descomposición ordenada de n en 3 sumandos le corresponde un término del
desarrollo. Veamos como ilustración el caso n = 3. Las posibles descomposiciones de 3 en tres
sumandos son (no ponemos los +):
300, 030, 003, 201, 210, 102, 120 y 111. Por ejemplo, la descomposición 120 se corresponde
3! 1 2 0
3
con el término P1,2,0
a1b 2 c 0 =
a b c = 3ab 2 .
1!0!2!
En el caso general, la potencia n-sima de un multinomio, (a1 + a2 + ... + ar )n , será:
(a1 + a2 + ... + ar )n =
∑
n1 + n2 +...+ nr = n
Pnn1 ,n2 ,...,nr a1n1 a2n2 ....arnr
Este ejemplo y su generalización nos indican que un problema combinatorio
de gran importancia es el cálculo de las particiones de números y conjuntos.
Así pasamos a la Combinatoria avanzada.
24
Combinatoria Avanzada: Particiones, Permutaciones y más Recurrencias
Particiones de conjuntos
Sea A un conjunto con n elementos. Una partición de A en k partes consiste en distribuir
los n elementos en k grupos (o cajas), de manera que ningún grupo quede vacío. Por
supuesto, ha de cumplirse que
0<k ≤n
Ejemplo: Sea A={a,b,c,d}, esto es, n=4. Si ponemos k=2 tendremos las siguientes siete
posibles distribuciones de A en dos partes (véase que el orden no cuenta):
a+bcd, b+acd, c+abd, d+abc, ab+cd, ac+bd, ad+bc
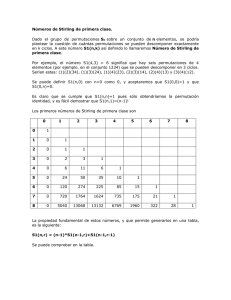
El número de particiones de n elementos en k grupos es un número de Stirling de segunda
clase, que se escribe en la forma siguiente:
Número de Stirling de segunda clase: S nk
En el ejemplo, S 42 = 7
25
Particiones de números
Sea n un número entero. Una partición de n en k partes consiste en escribir n como suma
de k sumandos, que pueden aparecer repetidos. En la teoría se suele exigir que ningún
sumando sea nulo (aunque en las potencias de polinomios sí que lo admitimos):
0<k ≤n
Ejemplo: Sean n = 5 y k = 3. Las posibles particiones son dos: 3+1+1 y 2+2+1, si no
tenemos en cuenta el orden de los sumandos. Sin embargo, en las aplicaciones hay que
considerar a veces el orden. En ese caso las posibles particiones serían 6: 3+1+1, 1+3+1,
1+1+3, 2+2+1, 2+1+2 y 1+2+2. Podemos dar una definición más refinada:
Una partición de n es una familia de k números, {n1 ≥ n2 ≥ ... ≥ nk } , mayores que 0,
k
tales que ∑ ni = n. (Recordar la fórmula de (a + b + c) n ...)
i =1
El número de particiones de n en k sumandos, sin el orden, se escribe: Pnk
En el ejemplo, P53 = 2 (5 = 3 + 1 + 1 y 5 = 2 + 2 + 1)
El número de particiones de n en k sumandos, contando el orden, se denota por: POnk
En el ejemplo, PO53 = 6 (5 = 3 + 1 + 1 = 1 + 3 + 1 = 1 + 1 + 3 y 5 = 2 + 2 + 1...)
26
Algunas observaciones
Para hallar POnk a partir de Pnk se razona así:
Tomemos una partición no ordenada cualquiera con k elementos. De esos, habrá
algunos grupos de elementos iguales. Por tanto, para hallar las particiones ordenadas
asociadas a la dada hay que calcular el número de permutaciones con repetición que le
corresponden, que dependerá de los elementos repetidos. Sumando después sobre todas
las particiones no ordenadas se halla el número de particiones ordenadas.
El “Principio del Palomar, (o del Casillero, o del Cajón…)” (Pigeonhole Principle)
Este principio es la sencilla observación de que (para particiones de conjuntos) cuando
n es mayor que k, al distribuir los n elementos en k grupos, en alguno de éstos hay más
de un elemento. Se usa en muchas demostraciones. Vea las hojas de ejercicios.
27
Permutaciones ordinarias y sus ciclos
Comenzamos con un ejemplo ilustrativo. Sea n = 3 y construyamos las 3! = 6
permutaciones ordinarias, pero escribiéndolas en forma de matriz de dos filas, donde en
la fila superior mantenemos los tres elementos en un orden fijado:
⎛123 ⎞
⎜
⎟,
⎝123 ⎠
⎛ 123 ⎞ ⎛ 123 ⎞ ⎛ 123 ⎞ ⎛ 123 ⎞ ⎛ 123 ⎞
⎜
⎟, ⎜
⎟, ⎜
⎟, ⎜
⎟, ⎜
⎟
⎝132 ⎠ ⎝ 213 ⎠ ⎝ 231⎠ ⎝ 312 ⎠ ⎝ 321⎠
En rojo se han marcado los “puntos fijos” y en azul los “ciclos” de 2 ó 3 elementos.
Así, tendremos que:
⎛123 ⎞
⎜
⎟ : En esta permutación todos los puntos son fijos
⎝123 ⎠
⎛ 123 ⎞
⎜
⎟ : Ésta se compone del ciclo 2 → 3 → 2 y un punto fijo
1
32
⎝
⎠
⎛ 123 ⎞
⎜
⎟ : Ésta corresponde al ciclo 1 → 2 → 3 → 1
231
⎝
⎠
28
Se observa que cualquier permutación se obtiene mediante una composición de ciclos de
diferentes longitudes, que pueden ir desde 1 hasta n (en el ejemplo, n = 3), luego:
⎛123 ⎞ ⎛ 123 ⎞ ⎛ 123 ⎞ ⎛ 123 ⎞ ⎛ 123 ⎞ ⎛ 123 ⎞
⎜
⎟, ⎜
⎟, ⎜
⎟, ⎜
⎟, ⎜
⎟, ⎜
⎟
⎝123 ⎠ ⎝ 132 ⎠ ⎝ 213 ⎠ ⎝ 231⎠ ⎝ 312 ⎠ ⎝ 321⎠
Se pueden escribir también de esta otra manera:
(1)(2)(3), (1)(23), (3)(12), (123), (132) y (2)(13)
Nótese que lo único que interesa son los ciclos que forman la permutación y que el
orden en que se escriben no tiene importancia.
Se plantea ahora el problema de contar cuántas permutaciones de n elementos existen
que se puedan escribir como combinación de k ciclos. Su número es un número de
Stirling de primera clase, y se escribe
snk
En el ejemplo, s31 = 2, s32 = 3, y s33 = 1
29
Relaciones de recurrencia para los números de Stirling
Para los números de segunda clase
Sea S nk el número de particiones de un grupo de n elementos en k bloques. Para
contarlas, elijamos un elemento fijo a. Pueden pasar dos cosas:
1. a constituye por sí sólo un bloque.
2. a no es un bloque por sí mismo.
En el primer caso, retiremos el bloque formado por a. Entonces nos quedarán k − 1 bloques
formados con los n − 1 elementos restantes. Se pueden formar S n -1,k -1 de ellos. Al añadir de nuevo
el bloque formado por a tendremos ya S n -1,k -1 de las S nk posibles particiones.
En el segundo caso, retiremos también el elemento a. Entonces nos quedarán k bloques
formados con los n − 1 elementos restantes. Se pueden formar S n -1,k de ellos. Al reponer el
el elemento a, que se puede ubicar de k modos distintos en cada permutación,
tendremos las restantes kS n -1,k de las S nk posibles particiones.
Luego hemos obtenido la ley de recurrencia S nk = S n -1,k −1 + kS n-1,k
30
El Triángulo de Stirling de 2ª clase
nk
0
1
2
3
4
5
6
…
0
1
1
0
1
2
0
1
1
3
0
1
3
1
4
0
1
7
6
1
5
0
1
15
25
10
1
6
0
1
31
90
65
25
1
7
0
1
33
201
350
190
31
1
8
0
1
…
…
…
…
…
…
…
n-1
n
…
k-1
k
…
…
…
Éste,
más
éste
por
dan
éste
S nk = S n −1,k −1 + kS n −1,k
31
Para los números de primera clase
Sea snk el número de permutaciones de n elementos descomponibles en k ciclos. Para
contarlas, elijamos un elemento fijo a. Pueden pasar dos cosas:
1. a constituye por sí sólo un ciclo, esto es, es un punto fijo.
2. a no es un ciclo por sí mismo, o sea, no es un punto fijo.
En el primer caso, retiremos el punto fijo a. Entonces nos quedarán k − 1 ciclos
formados con los n − 1 elementos restantes. Se pueden formar sn -1,k -1 de ellos. Al añadir de nuevo
el ciclo a tendremos ya sn-1,k -1 de las snk posibles permutaciones.
En el segundo caso, retiremos también el elemento a de todos los ciclo donde aparezca. Entonces
quedarán k ciclos formados con los n − 1 elementos restantes. Se pueden formar sn-1,k de ellos.
Al reponer a, que se puede ubicar de n − 1 modos distintos en cada permutación,
tendremos las restantes (n − 1) sn-1,k de las snk posibles particiones.
Luego hemos obtenido la ley de recurrencia s nk = sn -1,k −1 + (n − 1) sn-1,k
32
El Triángulo de Stirling de 1ª clase
n
k
0
1
2
3
4
5
6
…
0
1
1
0
1
2
0
1
1
3
0
2
3
1
4
0
6
11
6
1
5
0
24
50
35
10
1
6
0
120
274
225
85
15
1
7
0
720
176
4
1624
735
17
5
21
1
8
0
5040
…
…
…
…
…
…
…
…
k-1
k
…
…
…
Éste,
más
éste
por
n-1
dan
éste
n
snk = sn −1,k −1 + (n − 1) sn −1,k
(n-1)!
33
Leyes de Recurrencia (2)
Una familia ordenada –según los números naturales– de fórmulas F(n) se dice recurrente
o recursiva cuando la fórmula n-sima se puede obtener sistemáticamente a partir de un
número fijo de las anteriores. Habitualmente, la recurrencia utiliza un número pequeño
de fórmulas anteriores a la n-sima para establecer ésta. Ya hemos visto que un problema
de recurrencia completo está formado por una regla de recurrencia más el dato de
algunos valores iniciales.
La solución de un problema de recurrencia es una sucesión de números generada a partir
de los valores iniciales usando la ley recursiva de que se trate. Veamos un ejemplo:
⎧ F = F n −1
E l p r o b le m a d e r e c u r r e n c i a c o m p le t o f o r m a d o p o r ⎨ n
⎩ F0 = 2
t i e n e p o r s o lu c i ó n l a s u c e s i ó n n u m é r i c a {2 , 2 , 2 , 2 , . . . .} ,
p u e s la le y d e r e c u r r e n c i a d i c e q u e c a d a t é r m i n o e s i g u a l a l a n t e r i o r .
C o m o e l p r i m e r o q u e n o s d a n e s 2 , t o d o s lo s d e m á s v a le n i g u a l.
34
También puede considerarse la recurrencia sobre dos o más variables: Por ejemplo, el
Triángulo de Pascal muestra una fórmula recurrente sobre dos variables. La solución de
un problema completo de recurrencia sobre dos variables es una tabla de números
generada a partir de los valores iniciales usando la ley recursiva de que se trate.
La sucesión de Fibonacci
La sucesión de Fibonacci es la solución del siguiente problema de recurrencia:
⎧ Fn = Fn − 1 + Fn − 2
⎨
⎩ F0 = 0, F1 = 1
que es la sucesión num érica
{0,1,1,2,3,5,8,13,21,34,55,89,144,...} ,
pues la ley de recurrencia dice que cada térm ino es la sum a de los dos anteriores.
P or tanto hacen falta dos valores iniciales. Los elem entos de la sucesión se llam an
"núm eros de Fibonacci".
Una vez escrita la ley de recurrencia, hallar la sucesión es inmediato, pero se plantea este
problema: ¿Será posible dar una fórmula directa para el n-simo número sin tener que
pasar obligatoriamente por todos los anteriores?
35
Algunas herramientas matemáticas
a) Funciones generatrices
Una serie de potencias es una expresión
∑ a x . Cuando sea posible obtener una
n
n
serie de potencias a partir de alguna función f ( x ), diremos que la función f ( x ) es una
función generatriz de la sucesión de coeficientes {a0 , a1 , a2 ,...} .
1
, si efectuamos formalmente la división según la
1− x
regla de división de polinomios, obtenemos la serie 1 + x + x 2 + x 3 + ..., que podemos
Por ejemplo: Dada la expresión f ( x ) =
∞
también representar como
∑ a x . La sucesión de coeficientes es {1,1,1,1,...} , así que
n
n=0
f ( x) =
n
1
es función generatriz de {1,1,1,1,...} .
1− x
36
b) Desarrollo en fracciones simples: Un ejemplo ilustrativo
px + q
. Desarrollarla en fracciones simples
( x − a )( x − b )
px + q
A
B
=
+
consiste en calcular dos números A y B tales que
.
( x − a )( x − b ) x − a x − b
Los números A y B se hallan fácilmente operando y resolviendo un sistema de dos
Consideremos la expresión
ecuaciones con dos incógnitas:
⎧ A+ B = p
( A + B ) x − ( Ab + Ba )
A
B
px + q
+
=
=
⇒⎨
( x − a )( x − b )
( x − a )( x − b )
x−a x−b
⎩bA + aB = − q
Ejemplo:
⎧ A+ B =1
⎧ A = 1/ 2
x−2
x−2
luego ⎨
y por tanto
=
⇒⎨
−
+
=
2
=
3
/
2
A
B
B
x 2 − 1 ( x − 1)( x + 1)
⎩
⎩
x − 2 1/ 2 3 / 2
=
+
.
x2 − 1 x − 1 x + 1
37
Aplicación a la sucesión de Fibonacci: Función generatriz
Sea { F0 , F1 , F2 , F3 ,...} la sucesión de Fibonacci. Vamos a encontrar una función
generatriz para ella. Para hallarla, escribamos conjuntamente la ley de recurrencia
⎧ Fn = Fn −1 + Fn − 2
y las condiciones iniciales en una única ecuación: De ⎨
pasemos a
F
F
=
=
0,
1
1
⎩ 0
Fn = Fn −1 + Fn − 2 + [ n = 0, 0] + [ n = 1, 1] . Multipliquemos ahora toda la ecuación por
x n y sumemos sobre n desde 0 hasta ∞: Nos quedará:
∞
∞
∑F x = ∑F
n
n =0
n
n =0
∞
∑F x
n =0
n
∞
n
n −1
x + ∑ Fn − 2 x + ∑ {[ n = 0, 0] + [ n = 1, 1]} x n , o bien
= x ∑ Fn −1 x
n =1
∞
∞
n
n
n =0
n =0
n −1
+x
∞
2
∑F
n=2
n−2
x
n−2
∞
+ x. Si escribimos ahora f ( x) = ∑ Fn x n ,
n=0
obtendremos la "ecuación funcional" f ( x ) = xf ( x ) + x 2 f ( x ) + x, de donde:
(1 − x − x 2 ) f ( x) = x, luego f ( x) =
x
es la función generatriz buscada.
2
1− x − x
38
Aplicación a la sucesión de Fibonacci: Desarrollo en fracciones simples
−x
y apliquemos
2
x + x −1
la técnica de las fracciones simples. Para ello, resolvemos x 2 + x − 1 = 0 :
Escribamos la función generatriz como f ( x) =
−1 ± 5
, a cuyas soluciones llamaremos − ϕ y ϕ (el número ϕ se
2
llama "número de oro" o "divina proporción") . Las fracciones parciales
x=
A
A
B
ϕ
obtenidas son
y
. Si escribimos la primera en la forma
,
x
x +ϕ
x −ϕ
1+ ϕ
A
hallamos el desarrollo
ϕ
1 + ϕx
= ϕA ⎡1 − ϕx +
⎣⎢
( ) ( ) ...⎤⎦⎥ , y análogamente
x
ϕ
2
−
x
3
ϕ
para la otra. Sumando y juntando términos se obtiene la expresión de los
Fn , los coeficientes de x n en el desarrollo total: Acabarlo como ejercicio.
39
Las “Torres de Hanoi”, 1
El problema consiste en calcular el número de movimientos necesarios para pasar todos los discos de la
primera varilla a la segunda (o a la tercera) respetando las siguientes reglas:
• Sólo se puede mover un disco cada vez
• Los discos que haya en cualquier varilla han de estar ordenados por diámetros decrecientes hacia arriba.
El número de movimientos depende de la cantidad de discos. Si hay n discos,
M n representará el número de movimientos. Es claro que M 0 = 0 y M 1 = 1:
Varilla 1 Varilla 2 Varilla 3
Movts:
Varilla 1
Varilla 2
Varilla 3
0
Movts:
0
M0 = 0
1
M1 = 1
40
Las “Torres de Hanoi”, 2
Varilla 1 Varilla 2 Varilla 3
Movts:
Varilla 1
Varilla 2
Varilla 3
0
Movts:
0
1
1
2
2
3
M2 = 3
3
Tras el movimiento 2, estamos
en el caso de un único disco: un
movimiento más, y
terminamos…
4
M3 = 7
Tras el movimiento 4, estamos en el
caso de dos discos, así que con tres
movimientos más, acabamos…
41
Las “Torres de Hanoi”, 3
Ahora ya podemos formular la ley de recurrencia:
⎧ M n +1 = 1 + 2 M n
⎨
M0 = 0
⎩
Discos
0
1
2
3
4
…
Movs:
0
1
3
7
15
…
Si operamos un poco obtendremos una fórmula cerrada para M n :
M n = 1 + 2 M n −1 = 1 + 2(1 + 2 M n − 2 ) = 1 + 2 + 4 M n − 2 = 1 + 2 + 4(1 + 2 M n −3 ) =
= 1 + 2 + 3 + 4 + 8M n −3 = 20 + 21 + 22 + 23 M n −3 = ... =
= 20 + 21 + 22 + 23 + ... + 2k M n − k = 20 + 21 + 22 + 23 + ... + 2n −1 M 1 , y como
M 1 = 1, nos quedará, sumando la progresión geométrica de razón 2:
M n = 20 + 21 + 22 + 23 + ... + 2n−1 = 2n − 1
42