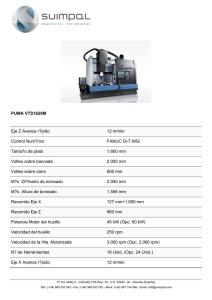
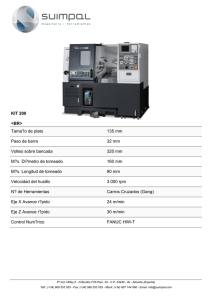
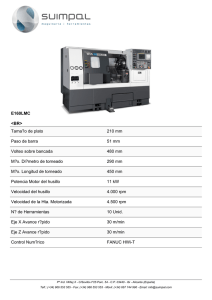
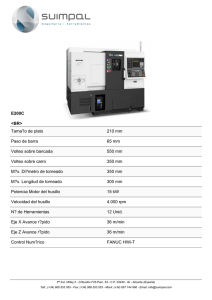
capitulo 1 ok a4

A = área; I = momento de inercia; i = radio de giro
NOTA: El momento de inercia con respecto a cualquier eje paralelo al eje que pasa por el centro de gravedad,
es igual al momento de inercia con respecto al centro de gravedad más el producto del área por el
cuadrado de la distancia perpendicular entre los dos ejes.
1. CUADRADO
Propiedades referidas al eje de gravedad
A = H2
C
H
G
G
C = H/2
IG = H4/12
iG = H/√12
H
2. RECTÁNGULO
Propiedades referidas al eje de gravedad
C
H
G
A = BH
G
C = H/2
IG = BH3/12
iG = H/√12
B
3. RECTÁNGULO HUECO
Propiedades referidas al eje de gravedad
C
A = BH - bh
H h G
G
C = H/2
IG = (BH3 - bh3)/12
iG = √(BH3 - bh3)/ 12A
b
B
PROPIEDADES DE ÁREAS PLANAS
ANEXO N°2 Propiedades de áreas planas
Grupo
Polpaico
Siempre en Obra
4. POLÍGONO REGULAR
Propiedades referidas al eje de gravedad.
y
b = 2R sen α
= 2 r tan α
α = 180˚/n; β = [(n-2)/n] x 180˚
r
b G
G
α
(n = nùmero de lados)
A = brn/2
R
β
IG = brn (6R2 - b2)/48
iG =
√(6R2 - b2)/ 24
y
5. RECTÁNGULOS IGUALES
Propiedades referidas al centro de gravedad
C
H
CG
G
h
G
A = B (H-h)
C = H/2
IG = B(H3 - h3)/12
iG
B
=
√(H3 - h3)/[12(H - h)]
6. TRIÁNGULO
Propiedades referidas al centro de gravedad
C
H
G
CG
G
A = BH/2
C = 2H/3
IG = BH3/36
iG = H/√18
B
287
Bs
A = [H (Bi+Bs)]/2
C = [H (2Bi+Bs)]/[3 (Bi+Bs)]
C
H
IG =
H3 (Bi2 + 4BiBs+Bs2)
36 (Bi + Bs)
G
G
Bi
8. CÍRCULO
Propiedades referidas al centro de gravedad
R
D
G
•
C
A = πD2/4 = πR2
C = D/2 = R
G
CG
IG = πD4/64
iG = D/4 = R/2
9. CORONA CIRCULAR
Propiedades referidas al centro de gravedad
C
De
288
Di
G
•
CG
G
A = π(De2- Di2)/4
C = De/2
IG = π(De4- Di4)/64
iG =
√(De2 + Di2)/4
PROPIEDADES DE ÁREAS PLANAS
7. TRAPECIO
Propiedades referidas al eje de gravedad
Grupo
Polpaico
Siempre en Obra
10. SEMICÍRCULO
Propiedades referidas al centro de gravedad
CG
R
C
G
4R/3π
G
A = πR2/2
C = R (1- 4/3π)
IG = (9π2 + 64)R4/72π
D
iG = R√(9π2 + 64)/6π
289