Ej. Campo eléctrico

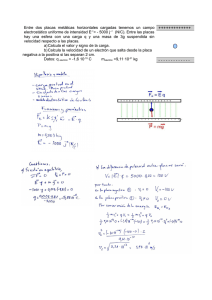
FÍSICA 2º
-
Ejercicios CAMPO ELÉCTRICO
-
Fecha : ……………….
1.- En los vértices de un cuadrado de lado 2 10-9 m se colocan cuatro protones. Otro protón está
inicialmente sobre la perpendicular al cuadrado por su centro, a una distancia de 2 10-9 m del
mismo. Calcular:
a) Velocidad inicial mínima que el quinto protón necesita para llegar al centro del cuadrado
b) Aceleración inicial y aceleración final del protón
c) Representar la energía potencial del protón en función de su distancia al centro del cuadrado
d) Describir el movimiento del protón en el caso de que la energía sea menor o mayor que la
que se deduce del apartado a)
2.- Una carga puntual de 4 C se encuentra localizada en el origen de coordenadas y otra carga
de -2 C en el punto (0,4) m . Suponiendo que se encuentran en el vacío, calcular:
a) La intensidad del campo eléctrico en el punto A (6,0) m
b) El potencial eléctrico en el punto A
c) La diferencia de potencial entre los puntos A y B (8,0) m
d) El trabajo necesario para llevar una carga de 3 C desde el punto A al punto B
3.- Dos esferas iguales, de masa m y carga q , están suspendidas del mismo punto por medio de dos
cuerdas de longitud l. Hallar el ángulo  que las cuerdas formarán con la vertical, una vez que se
alcance el equilibrio.
4.- Dos placas paralelas verticales están separadas por una distancia de 1 m y cargadas de forma
que sus potenciales respectivos son V1 = 600 voltios , V2 = - 400 voltios . Calcular :
a) Campo eléctrico entre las placas
b) Fuerza sobre una partícula de masa 1 mg y carga de +4 C colocada entre las placas
c) Trabajo necesario para llevar la partícula desde un punto A, situado a 20 cm de la placa V1,
hasta otro punto B, situado a 30 cm de la placa V2. Explicar el signo del trabajo.
d) Si la partícula se encuentra en reposo en el punto A, ¿ con qué velocidad llegará al punto B ?
5.- Se establece una diferencia de potencial de 1600 V entre dos placas paralelas separadas 4 cm.
Un electrón se libera de la placa negativa en el mismo instante en que un protón se libera de la
placa positiva. ( Suponer que el electrón y el protón están lo suficientemente alejados como para
que se pueda despreciar su interacción mutua )
a) ¿ A qué distancia de la placa positiva se cruzan ?
b) Comparar las velocidades de ambas partículas cuando inciden sobre las placas opuestas
c) Comparar sus energías
6.- Si entre las dos placas de un condensador plano separadas 3 cm entre sí, existe un campo
eléctrico uniforme de 7 10-4 N.C-1 :
a) ¿ Qué fuerza se ejercerá sobre un electrón situado en su interior ?
b) ¿ Qué aceleración adquiere el electrón ?
c) Si el electrón se desplaza, partiendo del reposo, de la placa negativa a la positiva
¿ qué velocidad y energía cinética posee al llegar a la placa positiva ?
* Datos: me = 9,1 10-31 kg , mp = 1,7 10-27 kg , e = 1,6 10-19 C , K = 9 109 N.m2.C-2
Emiliano González - IES Vicente Aleixandre (Pinto) - [email protected]
2
Física 2º
-
Repaso del Campo Eléctrico (ejercicios)
1.- Calcular el campo y el potencial en A.
Q1 = 5 mC , Q2 = -10 C
-
Fecha : ………………………..
6.- Calcular el campo y el potencial en los
puntos del plano A (a y b son placas paralelas
infinitas)
2.- Calcular el campo y el potencial en A.
Q1 = Q2 = -8 C
7.- Calcular el valor de Q sabiendo que  = 30º
3.- Calcular el campo y el potencial en A.
Q1 = -200 C , Q2 = 100 C
8.- Calcular E sabiendo que  = 10º y que la
carga es Q = 4C
4.- Calcular el campo y el potencial en A.
Q1 = Q3 = -2 C , Q2 = 4 C
9.- Se coloca un electrón con velocidad inicial
nula en un punto B situado a 120 mm de una
carga positiva de 0,001 C. Calcular con qué
velocidad llegará el electrón a un punto A
situado a 60 mm de la carga.
5.- Calcular el campo y el potencial en los
puntos del plano A (a y b son placas paralelas
infinitas)
10.- Se coloca un protón con velocidad inicial
nula en la placa positiva de un condensador de
placas paralelas. Calcular la velocidad con que
llegará el protón a la placa opuesta.
Los potenciales de las placas son +400 mV y
-200 mV respectivamente, y la separación entre
placas es de 2 mm.
Emiliano González - IES Vicente Aleixandre (Pinto) - [email protected]