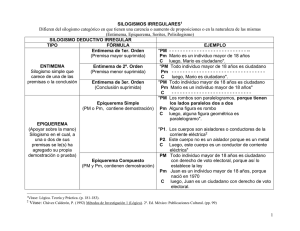
Epiquerema

TAREA 15 (APUNTES)
Nombre del alumno: ___________________________________________________ Grupo: _______
Ubicación en el Portafolio de evidencias
Campo disciplinar
Asignatura
Materia
Unidad
Tema
Subtema
SILOGISMOS ESPECIALES
Entimema
Es un silogismo abreviado en el cual falta una de las premisas. Para saber cuál de las premisas falta el
método es muy sencillo: hay que observar la conclusión. Recordemos que la conclusión se forma siempre
con el término menor más el término mayor. Ahora bien, si en la premisa se encuentra el término menor,
entonces falta la premisa mayor; y si en la premisa se encuentra el término mayor, entonces la premisa
que falta es la premisa menor.
Veamos dos ejemplos:
Juan es hombre
Juan es mortal
En este caso, el sujeto de la conclusión
es “Juan”. Entonces, “Juan” es el término menor (porque siempre el sujeto de
la conclusión es el término menor). Si
“Juan” se repite en la premisa, la premisa que nos dan es la premisa menor y
por lo tanto la premisa mayor es la que
falta.
Todo hombre es mortal
Juan es mortal
En cambio, en este caso vemos que el
término que se repite en la premisa es
el término mayor. Recordemos que el
predicado de la conclusión siempre es
el término mayor, en este ejemplo es
“mortal”. Ahora bien, si “mortal” está en
la premisa dada, esta premisa dada es
La mayor, y entonces falta la menor.
Ejercicio: escribe a la derecha de cada entimema la premisa que falta:
Todos los concursantes son becarios
Algunos alumnos de griego son becarios
_________________________________
Algunos diplomáticos no tienen chofer
Algunos diplomáticos no son embajadores
_________________________________
Todos los sospechosos son menores de edad
Algunos menores de edad son drogadictos
_________________________________
Algunos generales son clientes de gabriel
Algunos vegetarianos son generales
_________________________________
Epiquerema
El epiquerema es un silogismo cuyas premisas van acompañadas de una prueba. Si sólo una premisa
tiene prueba se llama “simple”, si las dos premisas tienen prueba se llama “doble”. Veamos un ejemplo:
Lo espiritual es indestructible, porque es simple
El alma humana es espiritual, porque es intelectual
El alma humana es indestructible
PRUEBA
PRUEBA
Podemos construir un epiquerema a partir de una conclusión dada. Los pasos son muy fáciles:
1. Se escribe la conclusión:
Todo hombre es libre
2. Se escriben el término menor y el término mayor en el lugar que les corresponde, suponiendo
que el silogismo es de la primera figura:
libre
Todo hombre
Todo hombre es libre
3. En los espacios que están en blanco inventamos un término medio y lo escribimos. Supongamos
que nuestro término medio será “todo ser inteligente” (tenemos que escribir “todo” y no “algún”
porque, si escribimos una premisa particular, la conclusión tendría que ser particular, por la
octava regla, y nuestra premisa es universal = todo hombre es libre):
Todo ser inteligente es libre
Todo hombre es ser inteligente
Todo hombre es libre
4. Una vez que tenemos el silogismo, para convertirlo en epiquerema añadimos una prueba, si
queremos que sea simple, o dos pruebas, si queremos que sea doble:
Todo ser inteligente es libre, porque sabe elegir
Todo hombre es ser inteligente, porque es racional
Todo hombre es libre
Ejercicio: ahora tú, construye un epiquerema a partir de la siguiente conclusión: “todo estudiante
disciplinado es un triunfador”:
Un epiquerema se puede descomponer en silogismos típicos si seguimos los siguientes pasos:
1. De cada premisa se puede derivar un silogismo completo.
2. La premisa mayor se descompone así: la primera premisa se forma con la prueba más el
predicado; la segunda premisa se forma con el sujeto más la prueba; la conclusión se forma
siguiendo las reglas generales que ya sabemos. Si tomamos como ejemplo el anterior
epiquerema, la premisa mayor se descompondría así:
Todo el que sabe elegir es libre
Todo ser inteligente sabe elegir
Todo ser inteligente es libre
3. La premisa menor también se descompone siguiendo los mismos pasos. Nótese que la
conclusión del primer silogismo típico es la premisa mayor original, y la conclusión de este
segundo silogismo típico es la premisa menor original:
Todo ser racional es ser inteligente
Todo hombre es ser racional
Todo hombre es ser inteligente
Ejercicio: descompón en silogismos típicos el siguiente epiquerema:
Todo hombre tiende a la perfección, porque ésta es parte de su naturaleza
Todo mexicano es hombre, porque posee racionalidad
Todo mexicano tiende a la perfección
Sorites
Es el silogismo compuesto de más de tres premisas dispuestas de tal manera que el predicado de la
primera pasa como sujeto de la segunda, el predicado de la segunda pasa como sujeto de la tercera, el
predicado de la tercera pasa como sujeto de la cuarta, y así sucesivamente.
Reglas:
1. Los términos que se repiten tienen que usarse en el mismo sentido y con el mismo significado
siempre.
2. Sólo la primera premisa puede ser particular.
3. Sólo la última premisa puede ser negativa
4. Debe tener como mínimo tres premisas, y puede tener como máximo las que se desee.
5. La conclusión se forma uniendo el primer sujeto con el último predicado.
Ejemplo:
1. Rocinante es un caballo
2. Todo caballo es cuadrúpedo
3. Todo cuadrúpedo es animal
4. Todo animal es viviente
 Rocinante es viviente
Conversión del sorites a silogismos simples
1.
2.
3.
4.
5.
6.
7.
La premisa 2 se escribe como si fuera la 1 y la 1 como si fuera la 2:
Se concluye según la regla general, y ya tenemos el primer silogismo típico.
Se escribe la siguiente premisa, en este caso la 3.
Se escribe la conclusión del anterior silogismo como premisa menor.
Se concluye según la regla general, y ya tenemos el segundo silogismo típico.
Se sigue con el mismo procedimiento hasta terminar las premisas.
Si la conclusión del último silogismo resultante es la misma que la del sorites, entonces hemos
hecho lo correcto y el sorites es válido.
1.
2.
3.
4.
Rocinante es un caballo
Todo caballo es cuadrúpedo
Todo cuadrúpedo es animal
Todo animal es viviente
 Rocinante es viviente
2. Todo caballo es cuadrúpedo
1. Rocinante es un caballo
 Rocinante es cuadrúpedo
3. Todo cuadrúpedo es animal
Rocinante es cuadrúpedo
 Rocinante es animal
4. Todo animal es viviente
Rocinante es animal
 Rocinante es viviente
Ejercicio: descompón el siguiente sorites en silogismos simples:
1. Todo estoico es disciplinado
2. El que es disciplinado es ordenado
3. El que es ordenado es metódico
4. El que es metódico es riguroso
5. El que es riguroso llega al éxito
 Todo estoico llega al éxito
Ejercicio: escribe un sorites con seis premisas