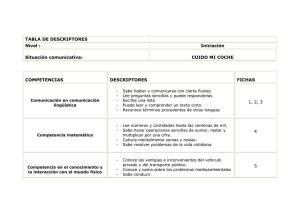
Punto crítico de una función escalar
Anuncio

Punto crítico de una función escalar
Publicado en Glosario Matemático (http://www.ub.edu/glossarimateco)
Punto crítico de una función escalar
Descripción: Dada una función escalar, \(f:{ A\subseteq \Re }^{ n }\longrightarrow \Re \), diferenciable,
siendo \(A\) un conjunto abierto de \({ \Re }^{ n }\), decimos que \(a\in A\) es un punto crítico de
\(f\) si cumple \(\triangledown f(a)=0\), es decir, el vector gradiente de \( f\) en el punto \(a\in A\) se
anula.
Descriptores: Óptimos Descriptores: Funciones de varias variables Descriptores: Funciones Funciones
Funciones de varias variables
Óptimos
Funciones
Funciones de varias variables
Óptimos
URL del envío:
http://www.ub.edu/glossarimateco/content/punto-cr%C3%ADtico-de-una-funci%C3%B3n-escalar
Powered by TCPDF (www.tcpdf.org)