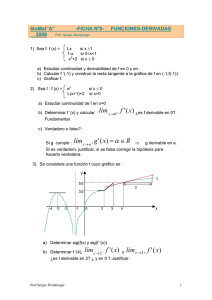
e x xgg )400 200()(: ∙ - = = )(: xff → )( xg )2( 6 g = 2
Anuncio

EXAMEN MAT 6toCB. Mat Cat “C” Tribunal: Balbier, Roballo, Weinberger 4/ 12 /13 Liceo Kennedy x 2 5x 4 x i) EAyRG de f (sin f ’’) 1) a) Sea f ( x) ii) Verificar que F ( x ) 1 2 x 5 x 4 L x es primitiva de f. 2 5 iii) Calcular e interpretar gráficamente: f 2 b) Sea g una función que cumple : d ( g ) R sig g ’ (x) x - - - 0 + + +? + +? + + + + -1 0 2 x 2 g ( 1) 2, g (3) 0 2 sig g ’’(x) + + + + 0 - - - - -------0 2 g (0) 3, lím x 0 1 e2x x R ii) EAyRG de g : g ( x) (200 x 400) e 2 x , sin g ’’ x2 3 b) Sea f : f ( x) si x 0 x 2 2 x si 0 x 2 (200 x 400) e 2 x si x 2 i) Estudiar continuidad y derivabilidad de f en 0 y en 2. ii) Graficar f. 2 i) Determinar si g es continua y derivable en 0 y 2. Fundamentar. ii) Graficar g, empleando todos los datos y deducir sig g(x) x g ( x ) g (0 ) 3 x 2) a) i) Verdadero o Falso?. Justificar: e 2 x g (x) 6 g (2)