J-06

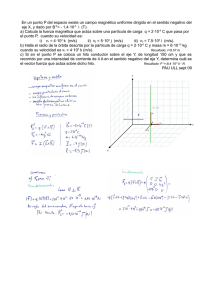
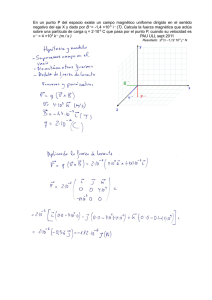
(J-06) Una partícula con carga 2.10-6 C se encuentra en reposo en el punto
(0,0). Se aplica un campo eléctrico uniforme de 500 N C -1 en el sentido
positivo del eje OY. a) Describa el movimiento seguido por la partícula y la
transformación de energía que tiene lugar a lo largo del mismo. b) Calcule la
diferencia de potencial entre los puntos (0,0) y (0,2) m y el trabajo realizado
para desplazar la partícula entre dichos puntos.
a)

a 


F e  q E (campo
eléctrico uniforme

(0,2)
(0,1)
v0=0
(0,0)
fuerza constante) ;

qE
m (constante) y v0 = 0. Al ser q >0 y m > 0 la aceleración tiene la
misma dirección y sentido que el campo eléctrico (sentido positivo del eje OY). El partir del
reposo obliga a la partícula a moverse en el sentido que le marca la aceleración (figura
adjunta; hacia arriba) y por lo indicado el movimiento es MRUA.
El ser la fuerza eléctrica conservativa y suponiendo que es la única presente, obliga a la
conservación de la energía mecánica.
F e  qE  2.10 6 .500  10 3 N (constante y hacia arriba)

NC  F ext
W 
F
W 
F e ; 0,00,2
 0  E M  Ec  Ep 

(  r  d
Ec  Ep
0,2   
  
  0,0 F e.d r  F e. r  q E . r  F e d  qEd (>0)
[El W es independiente del camino seguido]
Aplicando el teorema de las fuerzas vivas: W   W   Ec = qEd > 0.
FR
Fe
Aumenta linealmente con la distancia la energía cinética de la partícula (W=Ecf - Eci = Ecf
; v0 =0). Teniendo en cuenta las indicaciones anteriores y la ecuación del recuadro, disminuye
(linealmente con la distancia) la energía potencial eléctrica de la carga en lo mismo que
aumente la e. cinética en cualquier tramo recorrido o en los 2 metros totales.
................................
b)V(0,2)-V(0,0)

 20 
E .d r = 500.(0-2)=-1000 V.
De otro modo:
W  Ep e  V.q ; WFe= qEd = 2.10-6.500.2= - V.2.10 6 
Fe
V=-1000 V
-6
; WFe= qEd = 2.10 .500.2=
W   2.10 3 J
Fe

3 J

2.10
F e (“compensamos” la Fe )  W 
Fe
Si la fuerza a considerar es 
(recordemos que

E apunta hacia potenciales menores disminuye el potencial)