Una fabrica de automóviles, esta equipada para producir tres tipos

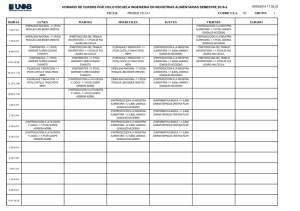
Fundamentos de Investigación de Operaciones.
22/08/2003
“Resolución de modelos de Programación Lineal y Análisis de Sensibilidad”.
Una fabrica de automóviles, esta equipada para producir tres tipos de automóviles, el
modelo X1, el modelo X2 y el modelo X3. Para ello se dispone al mes de 2400 horas de
trabajadores para ensamblaje y 600 horas para probar los modelos.
Los requerimientos de cada modelo se muestran a continuación.
Modelo
Horas requeridas de
montaje
Horas requeridas de
Prueba
Precio ($MM)
X1
4
2
7
X2
8
1
10
X3
8
2
12
MAX 7 X1 + 10 X2 + 12 X3
SUBJECT TO
2) 4 X1 + 8 X2 + 8 X3 <= 2400
3) 2 X1 + X2 + 2 X3 <= 600
END
a) Determine cual es el programa de producción óptimo utilizando el método Simplex.
b) Hasta cuanto podría disminuir la utilidad del modelo X3 sin que cambie la base óptima.
c) Usted es un fanático del modelo X2 (oX1), y desea que se fabriquen por lo menos 2
para comprarlos. Es tanto su deseo, que le ofrece al gerente de la fabrica trabajar gratis
ya sea en el área de montaje o de prueba. Con los conocimientos adquiridos en FIO
determine donde trabajar para conseguir su objetivo.¿ Cuántas horas se ofrecería, como
mínimo?.
d) Explique brevemente como podría resolver el problema anterior utilizando el método
gráfico visto en clases.(Recuerde que en el método Simplex son positivos, a lo sumo,
las variables básicas).
SOLUCIÓN:
Resolución por medio del método Simplex:
VB
Cj
X1
7
X2
10
X3
12
S1
0
S2
0
S1
S2
0
0
4
2
8
1
8
2
1
0
0
1
Zj
Cj-Zj
0
7
0
10
0
12
0
0
0
0
VB
Cj
X1
7
X2
10
X3
12
S1
0
S2
0
bj
bj/aj
X3
S2
12
0
0,5
1
1
-1
1
0
0,125
-0,25
0
1
300
0
600
0
Zj
Cj-Zj
6
1
12
-2
12
0
1,5
-1,5
0
0
3600
SOLUCIÓN 1
VB
Cj
X1
7
X2
10
X3
12
S1
0
S2
0
bj
bj/aj
X3
X1
12
7
0
1
1,5
-1
1
0
0,25
-0,25
-0,5
1
300
0
200
0
Zj
7
11
Cj-Zj
0
-1
Alternativamente se puede ingresar la variable X2 a la base
12
0
1,25
-1,25
1
-1
3600
bj
bj/aj
2400 300
600 300
0
SOLUCIÓN 2
VB
Cj
X1
7
X2
10
X3
12
S1
0
S2
0
bj
X3
X2
12
10
1,5
-1
0
1
1
0
-0,125
0,25
1
-1
300
0
Zj
Cj-Zj
8
-1
10
0
12
0
1
-1
2
-2
3600
25 puntos
b) Hasta cuanto podría disminuir la utilidad de X3 sin que cambie la base óptima
SOLUCIÓN 1
VB
Cj
X1
7
X2
10
X3
12
S1
0
S2
0
bj
X3
X1
12+D
7
0
1
1,5
-1
1
0
0,25
-0,25
-0,5
1
300
0
Zj
Cj-Zj
7
0
11
-1
12
0
1,25
-1,25
1
-1
3600
1)
2)
3)
-1-1,5D<=0
,25-0,25D<=0
-1+0,5D<=0
D>=-2/3
D>=-5
D<=2
Puede disminuir hasta en 2/3
SOLUCIÓN 2
VB
Cj
X1
7
X2
10
X3
12+D
S1
0
S2
0
bj
X3
X2
12+D
10
1,5
-1
0
1
1
0
-0,125
0,25
1
-1
300
0
Zj
Cj-Zj
8
-1
10
0
12
0
1
-1
2
-2
3600
1)
2)
3)
-1-1,5D<=0
1+0,125D<=0
-2-D<=0
D>=-2/3
D<=8
D>=-2
Puede disminuir hasta en 2/3
25 puntos
c) Usted es un fanatico del auto modelo X2 (o X1), y desea que se fabriquen por lo menos
2 para comprarlos. Es tanto su deseo, que le ofrece al gerente de la fabrica trabajar
gratis ya sea en montaje o prueba.
Con los conocimientos adquiridos en FIO determine donde trabajar (montaje o prueba),
para conseguir su objetivo.¿ Cuántas horas se ofrecería, como mínimo?
SOLUCIÓN 1
Del Tableau final se aprecia que la única actividad que aumenta la producción de
X1 es "Prueba".
 X 3   300 
 − 0.5   .... 

 = 
 + ∆S 2
 =  
 X1  0 
 1  2
⇒ ∆S 2 = 2
SOLUCIÓN 2
Del Tableau final se aprecia que la única actividad que aumenta la producción de
X2 es "Montaje".
 X 3   300 
 − 0.125   ....

 = 
 + ∆S1
 =  
 X 2  0 
 0.25   2 
⇒ ∆S1 = 8
25 puntos
e) Explique brevemente como podría resolver el problema anterior utilizando el método
gráfico visto en clases.(Recuerde que en el método Simplex son positivos, a lo sumo,
las variables básicas).
Como al menos una variable tiene valor cero, se tendrían que probar 3 casos.
1. X1=0; y resolver con método gráfico X2 y X3.
2. X2=0; y resolver con método gráfico X1 y X3.
3. X3=0; y resolver con método gráfico X1 y X2.
25 puntos