1 1- un autobus caracas- maracaibo ofrece plazas para

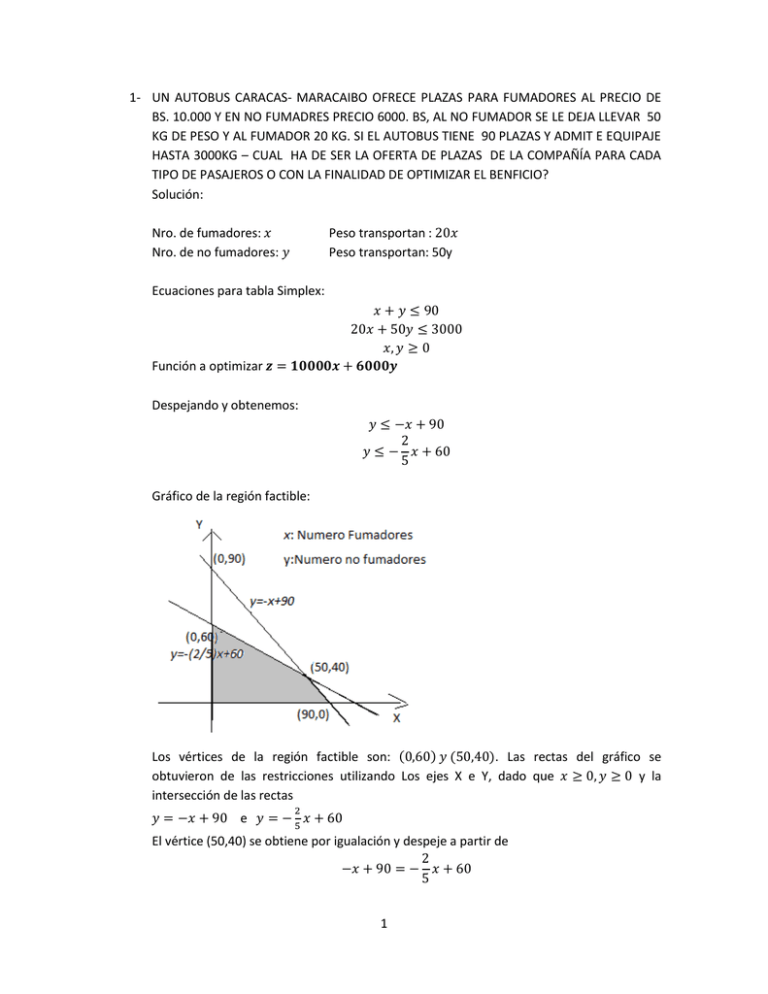
1- UN AUTOBUS CARACAS- MARACAIBO OFRECE PLAZAS PARA FUMADORES AL PRECIO DE
BS. 10.000 Y EN NO FUMADRES PRECIO 6000. BS, AL NO FUMADOR SE LE DEJA LLEVAR 50
KG DE PESO Y AL FUMADOR 20 KG. SI EL AUTOBUS TIENE 90 PLAZAS Y ADMIT E EQUIPAJE
HASTA 3000KG – CUAL HA DE SER LA OFERTA DE PLAZAS DE LA COMPAÑÍA PARA CADA
TIPO DE PASAJEROS O CON LA FINALIDAD DE OPTIMIZAR EL BENFICIO?
Solución:
Nro. de fumadores:
Nro. de no fumadores:
Peso transportan :
Peso transportan: 50y
Ecuaciones para tabla Simplex:
Función a optimizar
Despejando y obtenemos:
Gráfico de la región factible:
) (
Los vértices de la región factible son: (
). Las rectas del gráfico se
obtuvieron de las restricciones utilizando Los ejes X e Y, dado que
y la
intersección de las rectas
e
El vértice (50,40) se obtiene por igualación y despeje a partir de
1
De donde
De
y en consecuencia
.
, obtenemos
= 40
Según la teoría simplex, el valor Máximo de z, se obtiene en los vértices.
A continuación una tabla con los valores de z obtenidos en los vértices
x
y
0
60
360.000
50 40
290.000
90
0
900.000
En consecuencia el beneficio máximo se obtiene transportando 90 FUMADORES que van a
permitir un beneficio máximo de Bs. 900.000 y NINGUN No fumador.
2- UN SASTRE TIENE 80M2 DE TELA ALGODÓN Y 120 M2 DE TELA DE LANA. UN TRAJE
REQUIERE 1 M2 DE ALGODÓN Y 3 M2 DE LANA, Y UN VESTIDO DE MUJER REQUIERE
METRO CUADRADO DE CADA UNA DE LAS DOS TELAS, CALCULAR EL NUMERO DE TRAJES
Y VESTIDOS QUE DEBE CONFECCIONAR EL SASTRE PARA MAXIMIZAR LOS BENEFICIOS SI
UN TRAJE Y UN VESTIDO SE VENDE AL MISMO PRECIO.
Solución:
Nro. de trajes:
Nro. De vestidos:
Consumo algodón: x
Consumo algodón: y
Consumo lana: 3x
Consumo lana: y
Ecuaciones para tabla Simplex:
Función a optimizar
(variaría en una constante o sea
ya que trajes y vestidos se venden al mismo precio
(
) , que se optimizaría al optimizar
.
Despejando y obtenemos:
Función a optimizar obtenemos
2
Gráficos de la región factible:
Las fronteras de la región factible están en el primer cuadrante limitadas por el eje X, el
eje Y, y las rectas
)(
) (
Los vértices de la región factible son: (
). Las rectas del gráfico se
obtuvieron de las restricciones utilizando Los ejes X e Y, dado que
y la
intersección de las rectas
e
El vértice (20,60) se obtiene por igualación y despeje a partir de
De donde
De
y en consecuencia
, obtenemos
.
= 60
Según la teoría simplex, el valor Máximo de z, se obtiene en los vértices.
A continuación una tabla con los valores de z obtenidos en los vértices
x
y
0
80
80
20 60
80
40
0
40
En consecuencia el beneficio máximo se obtiene bien sea manufacturando 80 trajes o
manufacturando 20 trajes y 60 vestidos.
3
3- UNA COMPAÑÍA AEREA TIENE DOS AVIONES A Y B. PARA CUBRIR UN DETERMINADO
TRAYECTO. EL AVION A DEBE HACER MAS VECES EL TRAYECTO QUE EL AVION B PERO NO
PUEDE SOBREPASAR 120 VIAJES. ENTRE LOS 2 AVIONES DEBEN HACER MÁS DE 60 VUELOS
PERO NO MENOS DE 200. EN CADA VUELO A CONSUME 900 1 DE COMBUSTIBLE Y B 700
1. EN CADA VIAJE DE B. En cada viaje del avión A la empresa gana 300.000 pesetas y
200.000 por cada viaje del B. ¿CUANTOS VIAJES DEBE HACER CAD A AVION PARA OBTENER
EL MAXIMO DE GANANCIAS? ¿Cuántos VUELOS DEBE HACER CADA AVION PARA QUE EL
CONSUMO DE COMBUSTIBLE SEA MINIMO ?
Solución:
Nro. de viajes avión A:
Nro. de viajes avión B:
Consumo avión A: 900 l/viaje
Consumo avión B: 700 l/viaje
De las condiciones se sacan las siguientes ecuaciones:
Ecuaciones para tabla Simplex:
Función a optimizar
Para ganancia:
Para consumo de Combustible:
Despejando y obtenemos:
4
Gráfico de la región factible:
Las fronteras de la región factible están en el primer cuadrante limitadas por el eje X, el
eje Y, y las rectas
De la intersección de
y
,
obtenemos el punto (100,100).
De la intersección de
obtenemos el punto (130,70).
De la intersección de
De la intersección de
y
y
e
obtenemos el punto (60,0).
obtenemos (200,0)
Los vértices de la región factible son: (
La condición
) (
)(
).
obliga a que los vértices a estudiar sean (60,0),(120,0),(120,60)
Según la teoría simplex, el valor Máximo o mínimo de z, se obtiene en los vértices.
A continuación una tabla con los valores de z obtenidos en los vértices
x
y
60
0
17’946.000
54.000
120
0
35’892.000
108.000
120 60
47’850.000
150.000
5
En consecuencia el beneficio máximo de 47’850.000 se obtiene con 120 vuelos del avión A
y 60 vuelos del avión B. Mas si se tiene en cuenta solo el consumo mínimo de combustible,
esto será de 54.000 y se logrará con 60 vuelos del avión A y ningún vuelo del avión B.
4- Un hipermercado necesita como mínimo 16 Cajas de langostino 5 caja de necora 20
de percebes, 2 mayoristas A Y B, se ofrecen al hipermercado para satisfacer sus
necesidades pero solo venden dichos mariscos en contenedores completos
el mayorista A: envia en cada contenedor 8 cajas de langostino 1 de necora 2 de
perceberos
B: envia en cada contenedor 2, 10 y 7, respectivamente, cada contenedor que
suministra a:
A: cuesta 210.000 pecetas , mientras que los del mayorista B cuestan 300.000
pecetas cada uno.
para
satisfacer sus necesidades mínimas con el menor costo posible?
Solución:
Sean L, N y P, respectivamente, el numero requerido de Langostinos, Necoras y
Perceberos.
El contenido por contenedor de los proveedores A y B está en la siguiente tabla:
L
N
P
A
8
1
2
B
2
10
7
Las condiciones dadas nos llevan a las siguientes desigualdades:
Langostinos
Necora
Percebes
L:
N:
Las fronteras de estas restricciones son:
6
El grafico de estas restricciones es:
El único vértice para estas restricciones es (
)
El costo minimo se da por lo tanto para z= 210000x+300000y
=
139.375
Nota. Este problema debía tener soluciones enteras aproximadas. Porque la solución no es
entera.
7