Clase4DiscretizaciondeControladoresyPlan... 307KB Mar 01 2013

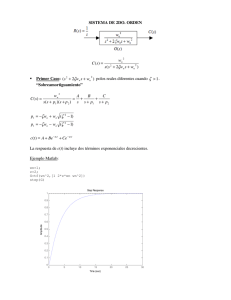
Control Automático
Discretización de reguladores y plantas
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Contenido
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
 Discretización a partir de la función de
transferencia en tiempo continuo




Por respuesta invariante al impulso
Por retenedor de orden cero (ZOH)
(
)
Por Tustin o transformación bilineal
Por mapeo de polos (solo para SISO)
 Ejemplos
 Ejercicios
Ej i i
1
2
3
4
Time (sec)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.5
Amplitude
Esquema de un control digital
0.4
0.3
0.2
0.1
0
0
1
2
3
y(t)
Computador
4
Time (sec)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Amplitude
Escogencia del periodo de
muestreo
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 El periodo de muestreo Ts debe ser escogido
para que sea menor que una décima parte de
la constante de tiempo dominante, del
sistema que se espera en lazo cerrado
1
Ts  Tdom.
10
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Amplitude
Escogencia del periodo de
muestreo
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Condiciones de la conversión
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
 Dos funciones continuas son discretizadas y se
encuentran en cascada
x(t)
X(s)
x*(t)
T X(z)
G1(s)
v(t)
V(s)
v*(t)
T V*(s)
V(z)
y(t)
Y(s)
G2(s)
y*(t)
T Y(z)
Y ((zz )
G( z) 
 G1 ( z )  G2 ( z )  ΖG1 ( s ) ΖG2 ( s )
X ( z)
 Dos funciones
f
continuas en cascada son
discretizadas; G(s) = G1(s)G2(s)
x(t)
X(s)
x*(t)
T X(z)
G1(s)
v(t)
V(s)
G2(s)
y(t)
Y(s)
Y ((zz )
G( z) 
 G ( s )  G1 ( s )G2 ( s )
X ( z)
y*(t)
T Y(z)
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Condiciones de la conversión
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
 Procedimiento:

x(t)
X(s)

Combinar todos los elementos continuos que se
encuentren directamente conectados en cascada
en una única función G(s)
y*(t)
y(t)
x*(t)
T X(z)
G1(((s)
K(z)
))
u*(t)
T U ((z))
G2(((s)
G(s)
))
T Y(z)
y(t)
Y(s)
Considerar como si la función G(s), tiene
además, paralelamente a su salida continua, una
( ) = Y(z)/U(z)
( ) ( )
salida muestreada. G(z)
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
El sistema híbrido de control
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
y(t)
r(t) +
x*(t)
R(s)
X(z)
-
T
G1(s)
K(z)
u*(t)
T U (z)
G2(s)
G(s)
5
y*(t)
T Y(z)
y(t)
Y(s)
H(s)
()
Y ( z)
K ( z )G ( z )
K ( z ) G ( s )
T ( z) 


R ( z ) 1  K ( z )GH ( z ) 1  K ( z ) G ( s ) H ( s )
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Amplitude
Transformación por respuesta
invariante al impulso
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)

Combinar
C
bi
ttodos
d llos elementos
l
t continuos
ti
que se
encuentren directamente conectados en cascada
en una única función G(s)
( )

Representar G(s) en fracciones parciales

Convertir
C
ti cada
d ffracción
ió parcial
i l a su fforma en Z
usando la transformada Z de la función exponencial
muestreada y con ayuda de tablas.
 
Le
 at
1

( s  a)
   e   1  e
e
 at
 akT
5
Tiene problemas de
aliasing
g
dependiente de T
1
 aT
z 1
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Respuesta invariante al impulso
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0

1
2
3
4
Time (sec)
P
Para
raíces
í
simples
i l
n
Ri
G( z)  
piT 1
(
1

e
z )
i 1

Para raíces repetidas
j
G( z)  
i 1

( 1)l 1 Ril  l 1 
1

l 1 
piT 1 
(
l

1
)!
(
1

e
z )
p

l 1

i
mi
No mantiene
N
ti
lla
respuesta ante
escalón. El factor
de escala es T
5
6
7
Impulse Response
0.7
0.5
Amplitude
Ejemplo 1: Discretización de
una planta por respuesta inv.
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Encuentre el modelo en tiempo discreto para
la planta P(s) mostrada, con T = 0.1s
4
P( s) 
( s  1)( s  4)
 Evaluando los residuos para los polos


P = [ -4 -1]
R = [-4/3 4/3]
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Ejemplo 1: cont.
cont
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Evaluando
Ri
4/3
4/3
P( z )  


piT 1
 4*0.1 1
1*0.1 1
z ) (1  e
z ) (1  e
z )
i 1 (1  e
2
 4 / 3* z
4 / 3* z
P( z ) 

( z  0.6703) ( z  0.9048)
0.31269 z
P( z ) 
( z  0.6703)( z  0.9048)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Por retenedor de orden cero
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
 Se combina la función de transferencia del
retenedor de orden cero con la de la planta.
y(k)
u(k)
1  e
Z
 s
u*(t)
ZOH
 sT
G(s)
( )

 G (s) 
* G ( s )  (1  z 1 ) * Z 

 s 

y(t)
Método preferible
para sistemas con
tiempo muerto
 El resultado se descompone en fracciones
parciales y cada fracción se transforma a Z.
6
7
Impulse Response
0.7
0.5
Amplitude
Ejemplo 2: Discretización de
una planta por ZOH
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Encuentre el modelo en tiempo discreto para
la planta P(s) mostrada, con T = 0.1s
4
P( s) 
( s  1)( s  4)
 Descomponiendo en fracciones parciales
P(s)/s los residuos y polos son:


R = [ 0.3333
0 3333 -1.3333
1 3333 1
1.0000]
0000]
P = [-4 -1 0]
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Ejemplo 2: cont.
cont
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Después de transformar cada fracción parcial
aplicando el periodo de muestreo T = 0.1s


0.33
1.33
1


P ( z )  (1  z ) 
( 4*0.1) 1
 (1*0.1) 1
0 1 
(
1

e
z
)
(
1

e
z
)
(
1

e
z )

1
 Sumamos,
S
aplicamos
li
ell ffactor
t (1 - z-11),
)
factorizamos y simplificamos:
0.01699 ( z+0.8466)
P( z ) 
, T  0.1s
( z-0.9048)( z-0.6703)
5
6
7
Impulse Response
0.7
0.5
Amplitude
Por el método de Tustin o
transformación bilineal
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
 Partimos de la relación de definición de z
z  e sT
 Despejamos s y desarrollamos la serie de
potencias
po
e c as de
del logaritmo
oga
o
No tiene p
problemas
de aliasing
dependiente de T
1
s  ln z
T
2 ( z  1) 2 ( z  1) 3
2 ( z  1) 5
s



3
5
T ( z  1) 3T ( z  1)
5T ( z  1)
 Finalmente aproximamos al primer término
2 ( z  1)
s
T ( z  1)
6
7
Impulse Response
0.7
0.5
Amplitude
Ejemplo 2: Discretización de
una planta por Tustin
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Encuentre el modelo en tiempo discreto para
la planta P(s) mostrada, con T = 0.1s
4
P( s) 
( s  1)( s  4)
 Sustituyendo
P( z ) 
4
2 ( z  1)
2 ( z  1)
(
 1)(
 4)
0.1 ( z  1)
0.1 ( z  1)
0.0079365( z  1) 2
P( z ) 
( z  0.6667)( z  0.9048)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.5
Amplitude
Por mapeo de polos y ceros
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
6
Solo para sistemas SISO. Se sustituye cada polo
de la forma (s - pi) por ( z – epiT ) y cada cero de
l fforma (s
la
( - zi) por ( z – eziT ).
) Finalmente
Fi l
t se
ajusta la ganancia K’ para una respuesta igual,
típicamente a frecuencia cero
cero. G ( s )
s 0  G ( z ) z 1
q
G ( s)  K
 (s  z )
i
i 1
n
 (s  p )
i
i 1
n>q
G ( z )  K ( z  1)
1
( n  q 1)
 =  en dom.
analógico   = ½ s
en el dom. discreto.
q
 (z  e
ziT
)
 (z  e
piT
)
i 1
n
i 1
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.5
Amplitude
Por mapeo de polos y ceros
0.4
0.3
0.2
0.1
0
0
La ganancia K’ se calcula como
n
K1  KB 
 (z  e
piT
)
i 1
( z  1)
( n  q 1)
q
 (z  e
i 1
K B  G ( s ) s 0  K
ziT
z 1
q
 z
)
i
i 1
n
 p
i
i 1
sT
Se satisface exactamente la relación z  e
1
2
3
4
Time (sec)
5
6
7
Impulse Response
0.7
0.5
Amplitude
Ejemplo 4: Discretización de
una planta por mapeo z = esT
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Encuentre el modelo en tiempo discreto para
la planta P(s) mostrada, con T = 0.1s
4
P( s) 
( s  1)( s  4)
 Los datos del sistema continuo son:



P = [-4 -1 ]
n = 2; q = 0
KB = P(0) = 1
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.5
Amplitude
Ejemplo 4: cont.
cont
0.4
0.3
0.2
0.1
0
0
 Evaluamos las fórmulas
P ( z )  K * Pˆ ( z )
1
Pˆ ( z ) 
( z  1)
- 4* 0 .1
-1* 0 .1
(z  e
)(z  e
)
Pˆ (1)  63.7486
( 2 - 0 -1)
K 1  1 / 63.7486
0.015687( z+1)
P( z ) 
, T  0.1s
( z-0.6703)( z-0.9048)
1
2
3
4
Time (sec)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.5
Amplitude
Respuesta al impulso
0.4
0.3
0.2
0.1
0
0
2
3
4
Time (sec)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Pt ti
Ptustin
Pmatched
0.6
0.5
Am
mplitude
Se puede
observar
b
que
solamente la
forma
invariante al
impulso
conserva este
tipo de
respuesta
t
1
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.5
Amplitude
Respuesta al escalón
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
6
7
Step
p Response
p
1
A
Amplitude
Todas las
f
formas
conservan la
respuesta ante
un escalón
excepto la
invariante al
impulso, que lo
h
hace
solo
l sii es
escalada por T
P
Pzoh
Ptustin
P
Pmatched
h d
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
Time (sec)
4
5
6
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.5
Amplitude
Respuesta ante rampa
0.4
0.3
0.2
0.1
0
0
2
3
4
Time (sec)
5
6
7
Respuesta ante rampa
3
2.5
2
A
Amplitude
Todas las
f
formas
conservan la
respuesta ante
una rampa
excepto la
invariante al
impulso.
1
1.5
P
Pzoh
PTustin
Pmatched
1
0.5
0
0
0.5
1
1.5
2
Time (sec)
2.5
3
3.5
4
Impulse Response
0.7
0.5
Amplitude
Ejemplo 5: Discretización del
regulador PID
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 El PID ideal se puede discretizar por los
métodos de

La aproximación
p
trapezoidal
p
a la integral
g y la
aproximación de Euler a la derivada

Transformación bilineal o método de Tustin
((s  z  kT))
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Amplitude
Discretización del PID por
aproximaciones a la I y D
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
6
 Partimos de la expresión para el PID en el
dominio del tiempo continuo
t
d
m(t )  K P e(t )  K I  e( )d  K D e(t )  m0
dt
0
 Obtenemos la forma posicional del algoritmo
del PID
e(k )  e(k  1)
 (e(k )  e(k  1)Ts

 Int prev.   K d
 m0
m ( k )  K P e( k )  K i 
Ts
2


7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Amplitude
Discretización del PID por
transformación bilineal
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
5
6
7
 Partimos
P ti
de
d lla expresión
ió para ell PID en ell
dominio de la frecuencia compleja
KP
K PID ( s )  K P 
 s  K PTd
Ti s
2 ( z  1)
 Sustituimos
s
T ( z  1)
y obtenemos la forma de velocidad del
algoritmo
l it
d
dell PID
K PTs
K PTd
e(k )  2e(k  1)  e(k  2)
m(k )  m(k  1)  K P e(k )  e(k  1) 
e( k ) 
Ti
Ts
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Amplitude
La forma de velocidad del PID
discreto
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 La forma de velocidad del PID se puede
simplificar a
m(k )  m(k  1)  A  e(k )  B  e(k  1)  C  e(k  2)
donde las constantes A, B y C dependen de
KP, Ti, Td y del tiempo de muestreo TS
 También se puede llegar a esta forma si
restamos la forma posicional del PID
evaluada en k y en k-1
 Esta forma es menos propensa al windup
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Ejercicios
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Obtenga y compare los modelos discretos,
con el periodo de muestreo T dado para las
funciones G(s), F(s) y H(s); por los cuatro
métodos vistos en clase.
3 * e  s*0.4
G ( s) 
; T  0.2s
( s  1)( s  2)
( s  0.4)( s  3)
F (s) 
; T  0.05s
s ( s  9)
( s  3)
H (s) 
; T  0.1s
2
s ( s  1)
5
6
7
Impulse Response
0.7
P
Pimp
Pzoh
Ptustin
Pmatched
0.6
Referencias
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0
1
2
3
4
Time (sec)
 Bollinger,
B lli
JJohn
h G
G., D
Duffie,
ffi N
Neilil A
A.. “C
“Computer
t C
Control
t l off
Machines and Processes”, Addison-Wesley, USA, 1988.
 Kuo, Benjamin C.. „Sistemas de Control Automático“,
Automático , Ed. 7,
Prentice Hall, 1996, México.
 http://www.ie.itcr.ac.cr/einteriano/control/clase/3.0SistemasdeCo
ntrolenTiempoDiscreto.pdf
t l Ti
Di
t df
 http://www.mathworks.com/access/helpdesk/help/toolbox/contro
l/manipmod/f2 3161 html
l/manipmod/f2-3161.html
5
6
7