Calcular la media, mediana y moda de un grupo de números

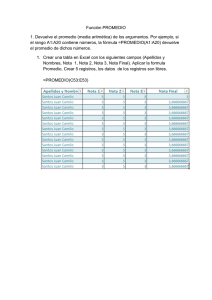
Universidad Pedagógica Experimental Libertador
Instituto Pedagógico de Miranda José Manuel Siso Martínez
Departamento de Ciencias Naturales y Matemáticas
Cátedra: Estadística aplicada a la educación
Estadística descriptiva con Excel
(Cálculo de medidas)
Prof. Cruz R. Guerra
1
Introducción
La sociedad mundial ha experimentado cambios globales que han afectado las
diversas áreas del quehacer social, cultural y económico. Entre los cambios más notables se
ubica el acelerado y exacerbado uso del computador en las labores diarias, en el desempeño
laboral así como en el desarrollo profesional. Es así como en la estadística se distingue el
uso de paquetes computacionales que elaboran con mayor facilidad, sencillez y rapidez los
cálculos estadísticos, gráficos y tablas de frecuencias. Entre estos programas se localizan:
STAT, GRAPH y SPSS. Las hojas de cálculo tienen potencialidades que pueden ser
aplicadas en el cálculo numérico.Excel no es un programa exclusivo para procesar datos
estadísticos sin embargo posee un conjunto de recursos que posibilitan el cálculo de las
medidas de tendencia central, las medidas de dispersión, las medidas de posición y las
medidas de forma, así como la elaboración de gráficos de distinta naturaleza. Es en este
sentido que Excel se muestra como un poderoso programa que proporciona herramientas y
funciones eficaces que pueden utilizarse para realizar análisis estadístico. De allí que el
presente material tenga como propósito explicitar los procedimientos para elaborar los
cálculos de las medidas estadísticas a través de Excel a fin de facilitar su aprendizaje.
2
Calcular la media, mediana y moda de un grupo de números
Media Devuelve el promedio (media aritmética) de los argumentos.
Sintaxis
PROMEDIO(matriz)
Matriz es la matriz o rango de datos que define la posición relativa.
Moda Devuelve el valor que se repite con más frecuencia en una matriz o rango de datos
Sintaxis
MODA(matriz)
Matriz es la matriz o rango de datos que define la posición relativa.
Mediana Es el número intermedio de un grupo de números; es decir, la mitad de los
números son superiores a la mediana y la mitad de los números tienen valores menores que
la mediana.
Sintaxis
MEDIANA(matriz)
Matriz es la matriz o rango de datos que define la posición relativa.
Ejemplo: cálculo de media, moda y mediana con Excel
Inicie Excel. En la Hoja1 transcriba los datos de la columna ”A”.
A
1
Datos
2
5
3
7
4
9
5
5
6
3
7
4
8
=PROMEDIO(A2:A7)
Media de todos los números de la lista anterior
9
=MODA(A2:A7)
Moda de todos los números de la lista anterior
10
=MEDIANA(A2:A7)
Mediana de todos los números de la lista anterior
Al final se observan los siguientes resultados.
A
8
5,5
9
5
10
5
Si realiza los cálculos con más datos, recuerde transcribir el rango exactamente de
forma tal que considere todos los datos Ej: (a2:a25) (a5:a34).
3
Calcular percentil y cuartil de un grupo de números
Percentil: Devuelve el k-ésimo percentil de los valores de un rango. Esta función permite
establecer un umbral de aceptación. Por ejemplo, podrá revisar a los estudiantes cuya
calificación sea superior al nonagésimo percentil.
Sintaxis
PERCENTIL(matriz;k)
Matriz es la matriz o rango de datos que define la posición relativa.
K es el valor de percentil en el intervalo de 0 a 1, inclusive
Cuartil: Devuelve el cuartil de un conjunto de datos. Los cuartiles se usan con frecuencia
en los datos de ventas y encuestas para dividir las poblaciones en grupos. Por ejemplo,
puede utilizar la función CUARTIL para determinar el 25 por ciento de ingresos más altos
en una población.
Sintaxis
CUARTIL(matriz;cuartil)
Matriz es la matriz o rango de celdas de valores numéricos cuyo cuartil desea
obtener.
Cuartil indica el valor que se devolverá
Ejemplo: cálculo de percentil y cuartil con Excel
Inicie Excel. En la Hoja1 transcriba los datos de la columna ”A”.
A
1
Datos
2
5
3
3
4
7
5
6
6
6
7
8
8
3
9
=PERCENTIL(A2:A8;0,3)
10
=CUARTIL(A2:A8;1)
El percentil 30 de la lista anterior
Primer cuartil (percentil 25) de los datos anteriores
Al final se observan los siguientes resultados.
A
8
9
4,6
10
4
Si realiza los cálculos con más datos, recuerde transcribir el rango exactamente de
forma tal que considere todos los datos Ej: (a2:a25) (a5:a34).
4
Calcular Varianza y desviación típica de un grupo de números
Varianza: Devuelve la varianza de los valores de un rango. Esta función permite calcular
la varianza de una muestra.
Sintaxis
VAR(número1;número2; ...)
Número1, número2,... son de 1 a 255 argumentos numéricos correspondientes a
una muestra de una población.
Desviación típica: Calcula la desviación estándar de una muestra. La desviación estándar
es la medida de la dispersión de los valores respecto a la media (valor promedio).
Sintaxis
DESVEST(número1; número2; ...)
Número1, número2,... son de 1 a 255 argumentos numéricos correspondientes a
una muestra de una población. También puede utilizar una matriz única.
Ejemplo: cálculo de varianza y desviación típica con Excel
Inicie Excel. En la Hoja1 transcriba los datos de la columna ”A”.
A
1
Pesos
2
13,45
3
13,01
4
13,68
5
13,22
6
13,7
7
12,7
8
13,18
9
13,25
10
13,63
11
12,99
12
=VAR(A2:A11)
13
=DESVEST(A2:A11)
Varianza
Desviación estándar
Al final se observan los siguientes resultados.
A
12
0,110632
13
0,3326142
Si realiza los cálculos con más datos, recuerde transcribir el rango exactamente de
forma tal que considere todos los datos Ej: (a2:a25) (a5:a34).
5
Calcular la curtosis y asimetría de un grupo de números
Curtosis: La curtosis caracteriza la elevación o el achatamiento relativo de una
distribución, comparada con la distribución normal. Una curtosis positiva indica una
distribución relativamente elevada, mientras que una curtosis negativa indica una
distribución relativamente plana.
Sintaxis
CURTOSIS(número1;número2; ...)
Número1, número2... son de 1 a 255 argumentos cuya curtosis desea calcular.
También puede utilizar una matriz única.
Asimetría: La asimetría de una distribución caracteriza el grado de asimetría de una
distribución con respecto a su media. La asimetría positiva indica una distribución
unilateral que se extiende hacia valores más positivos. La asimetría negativa indica una
distribución unilateral que se extiende hacia valores más negativos.
Sintaxis
COEFICIENTE.ASIMETRIA(número1;número2; ...)
Número1, número2... son de 1 a 255 argumentos cuya asimetría desea calcular.
También puede utilizar una matriz única.
Ejemplo: cálculo de curtosis y asimetria con Excel
Inicie Excel. En la Hoja1 transcriba los datos de la columna ”A”.
A
1
Datos
2
3
3
4
4
5
5
2
6
3
7
4
8
5
9
6
10
4
11
7
12
=CURTOSIS(A2:A11)
13
=COEFICIENTE.ASIMETRI
Curtosis del conjunto de datos anterior (-0,1518)
Asimetría del conjunto de datos anterior (0,359543)
A(A2:A11)
6
Realizar análisis estadístico con las Herramientas para análisis
Los cálculos referidos a las medidas de tendencia central, medidas de posición,
medidas de dispersión y medidas de forma explicados anteriormente pueden ser elaborados
de una manera más sencilla y rápida. Si tiene que desarrollar análisis estadístico puede
ahorrar pasos y tiempo si utiliza las Herramientas para análisis.
Las Herramientas para análisis incluye la opción de Análisis de datos.
En el caso de que el sistema operativo sea Windows XP la opción de Análisis de datos se
ubica en el menú Herramientas. Si la opción Análisis de datos no está disponible, deberá
cargarla seleccionando en el menú Herramientas la opción Complementos... Allí debes
señalar la casilla que identifica Herramientas para el análisis.
Una vez cargada la herramienta podemos activar la opción Análisis de datos del
menú Herramientas. Allí se muestra una ventana que te permite realizar distintos
análisis. Los de mayor utilidad para el curso de Estadística aplicada a la educación son:
Estadística descriptiva e Histograma.
Estadística descriptiva
La herramienta de análisis Estadística descriptiva genera un informe estadístico de
una sola variable para los datos del rango de entrada, y proporciona información acerca de
la tendencia central, dispersión de los datos y la forma de los datos.
Si se desea obtener las medidas de tendencia central, dispersión y forma de manera rápida
debemos hacer uso de esta opción.
1. Seleccionar Opción Análisis de datos del menú Herramientas
2. En la ventana que aparece (Análisis de datos) se debe seleccionar la opción
Estadística descriptiva
7
Posteriormente, en la ventana que se muestra debes seleccionar el Rango de
entrada. Suponiendo que los datos se encuentran en el rango que va desde A2 a A21
(A2:A21). En el Rango de salida se escribe la celda en donde se quieren los resultados. En
este caso se ha escrito D1. Finalmente se selecciona la opción Resumen de estadísticas, Késimo mayor y K-ésimo menor. Al finalizar presione Aceptar.
Se muestran resultados como en el ejemplo siguiente:
8
Histograma
La herramienta de análisis Histograma calcula las frecuencias individuales y
acumulativas de rangos de celdas de datos y de clases de datos. Esa herramienta genera
datos acerca del número de apariciones de un valor en un conjunto de datos. Asimismo,
posibilita la creación de un gráfico (Histograma).
Por ejemplo, en una clase con 20 alumnos, puede determinarse la distribución de
calificaciones y elaborar un histograma. Una tabla de frecuencias presentará los límites de
las calificaciones así como el número de calificaciones que haya entre el límite mínimo y el
límite actual. También presentará Histograma de las calificaciones.
17
15
19
18
17
9
14
11
10
17
15
11
17
14
12
15
5
13
15
16
Al usar Excel para construir una distribución de frecuencia y un histograma para estos
datos se deben elaborar las clases.
1. Introduzca los datos en la columna A, desde la fila 2 hasta la 21.
2. En la columna B, desde la fila 1 hasta 5, introduzca los límites superiores reales de cada
clase (7, 10, 13, 16, 19). Estos valores que ingresó en la columna B es lo que Excel
próximamente reconocerá como Rango de clases (Bin Values).
3. Seleccione el menú Herramientas. Escoja la opción Análisis de datos
9
En la ventana Análisis de datos, escoja la opción de Histograma. Presione
Aceptar y continúe con el próximo paso.
4. Introduzca las celdas correspondientes en la ventana que se muestra. De acuerdo al
ejemplo el Rango de entrada sería de la A2 a la A21 (A1:A21). Esto puede hacerse
escribiendo la localización o seleccionando el rango directamente desde la hoja.
Introduzca las celdas que se correspondan con los limites superiores (B1:B5) en el
Rango de clases. Lo próximo en la ventana del histograma sería especificar el Rango
de salida. Se ha escogido la columna D como el lugar donde empezarían nuestros
resultados, escribiendo D1 en la línea del Rango de salida. También, tenemos la
alternativa en Excel, de que los resultados aparezcan en otra hoja de trabajo.
Finalmente, para poder generar el histograma y la distribución de frecuencias se deben
escoger las opciones Porcentaje acumulado y Crear gráfico. Presione Aceptar.
10
.En la celda designada se muestra la siguiente información
Clase
7
10
13
16
19
y mayor...
Frecuencia
1
2
4
7
6
0
%
acumulado
5,00%
15,00%
35,00%
70,00%
100,00%
100,00%
Esta es la distribución de frecuencias. Solo debes incorporar los límites inferiores a
las clases, dando clic a las celdas d2, d3, d4, d5 y d6 respectivamente. En cada una de ellas
debes modificar la celda, escribiendo la clase correctamente (en vez de 7 se transcribe 5 - 7,
en vez de 10 se transcribe 8 – 10, en vez de 13 se transcribe 11 – 13, en vez de 16 se
transcribe 14 – 16 y en vez de 19 se transcribe 17 -- 19). Es recomendable que antes de
modificar las celdas con las clases (d1:d5) se debe cambiar el Formato de celdas y
manejarlo como tipo Texto.
En cuanto al gráfico se observa que las barras en el histograma están separadas
cuando estos rectángulos que se levantan sobre el eje horizontal deben ser continuos. Para
corregir este detalle, haga clic en cualquiera de las barras del histograma y seleccione el
menú Formato que aparece en la parte de arriba de su hoja de trabajo. Marque la opción
de Serie de datos seleccionada... Seleccione la pestaña Opciones de la ventana de
Formato de serie de datos (ver figura). La opción que permitirá que las barras se unan es
la selección de Ancho del rango. Cambie el ancho del rango a 0 para que no exista
separación entre las barras. En ese momento debe aprovechar y hacer los ajustes necesarios
para presentar su gráfica lo más explícita posible. Luego presione Aceptar.
11
12