PRIMERA CONDICIÓN DE EQUILIBRIO Un cuerpo
Anuncio

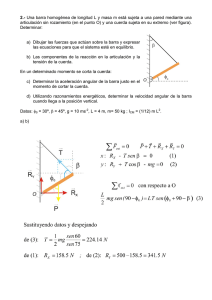
PRIMERA CONDICIÓN DE EQUILIBRIO Un cuerpo se encuentra en estado de equilibrio translacional si y sólo si la suma vectorial de las fuerzas que actúan sobre él es igual a cero. Obtenemos una segunda ecuación sumando las fuerzas a lo largo del eje Y, por lo tanto tenemos: Cuando un cuerpo está en equilibrio, la resultante de todas las fuerzas que actúan sobre él es cero. En este caso, Rx como Ry (Cos 30° + cos 50°) = 0.8660A + 0 .6427B = 300N (2) debe ser cero; es la condición para que un cuerpo esté en equilibrio: En las ecuaciones 1 y 2 se resuelven como simultanea A y B mediante el proceso de sustitución. Si despejamos A tenemos: A = 0.7660 / 0.5; A = 1.532B ; EJEMPLO: Una pelota de 300N cuelga atada a otras dos cuerdas, como se observa en la figura. Encuentre las tensiones en las cuerdas A, B Y C. SOLUCIÓN: El primer paso es construir un diagrama de cuerpo libre Ahora vamos a sustituir esta igualdad en la ecuación 2 0.8660(1.532B) + 0.6427B = 300N Para B tenemos: 1.3267B + 0.6427B = 300N 1.9694B = 300N, B= 300N / 1.9694, B= 152.33N Para calcular la tensión en A sustituimos B = 152.33 N A = 1.532(152.33N) = 233.3N La tensión en la cuerda C es 300N , puesto que debe ser igual al peso. Una pelota de 100N suspendida por una cuerda A es tirada hacia un lado en forma horizontal mediante otra cuerda B y sostenida de tal manera que la cuerda A forma un ángulo de 30° con el poste vertical ¿ encuentre las tensiones en las cuerdas A y B. Al sumar las fuerzas a lo largo del eje X, obtenemos: ∑ Fx = -A cos 60° + B cos 40° = 0 Al simplificarse por sustitución de funciones trigonométricas conocidas tenemos: -0.5A + 0.7660B = 0 (1) SOLUCIÓN Primero dibujamos le diagrama cuerpo libre: Ahora se aplica la primera condición de equilibrio. La suma de las fuerzas a lo largo del eje X: ∑Fx = B – A cos 60° = 0; B = A cos 60° = 0.5 A (1) Ahora al sumar las componentes en Y: ∑ Fy = A sen 60° - 100N = 0 4 calcule las tensiones en las cuerda “A” y “B” del sistema Por lo que: A sen 60° = 100N mostrado. Ahora se despejan las fuerzas desconocidas: (sen 60° = 0.8660) = 0.8660 A = 100N; A = 100N / .8660 = 115N Conocemos el valor de A, ahora despejamos B de la ecuación 1:B = 0.5 A = (0.5)(115N) = 57.5N ACTIVIDAD: Resuelva los siguientes ejercicios 1- Una pelota de 250N cuelga atada a otras dos cuerdas, como se observa en la figura. Encuentre las tensiones en las cuerdas A, B Y C. 2- Una pelota de 250N suspendida por una cuerda A es tirada hacia un lado en forma horizontal mediante otra cuerda B y sostenida de tal manera que la cuerda A forma un ángulo de 40° con el poste vertical ¿ encuentre las tensiones en las cuerdas A y B. 3 Una pelota de 300N suspendida por una cuerda A es tirada hacia un lado en forma horizontal mediante otra cuerda B y sostenida de tal manera que la cuerda A forma un ángulo de 45° con el poste vertical ¿ encuentre las tensiones en las cuerdas A y B. 5.-Encuentre la tensión el cable “A” y la compresión en el soporte “B” en la siguiente figura, si el peso es de 95 N. INSTITUTO TECNICO MARIA INMACULADA AREA: CIENCIAS NATURALES ASIGNATURA: FISICA TEMA: SEGUNDA CONDICION DE EQUILIBRIO GRADO: 10º INDICADORES DE DESEMPEÑO: * Aplico el concepto de torque o momento de fuerza. * Identifico y aplico la segunda condición de equilibrio (equilibrio rotacional). * Comunico ideas físicas orales y escritas, y cumplo con las labores asignadas. Matemáticamente, para el caso de fuerzas coplanares, se debe cumplir que la suma aritmética de los momentos relacionados con rotaciones anti - horarias debe ser igual a la suma aritmética de los momentos relacionados con INFORMACION rotaciones horarias. TORQUE O MOMENTO DE FUERZA: En general, un cuerpo se encontrará en equilibrio traslacional y equilibrio rotacional cuando se cumplen las dos condiciones de equilibrio. Es una magnitud vectorial cuando las fuerzas actúan sobre los cuerpos, pueden alterar su movimiento lineal o su rotación. El efecto de una fuerza dado sobre el movimiento de rotación de un cuerpo depende del valor de la fuerza, de la distancia del punto de aplicación de la fuerza al eje de giro y de la dirección de la fuerza con respecto a la línea que une el punto de aplicación de esta con el eje de giro generalmente se considera un toque positivo cuando tiende a producir rotación en sentido contrario a las manecillas del reloj y negativo en sentido de las manecillas del reloj. UNIDADES DE TORQUE S.I: “ M. K. S” Como el torque es el producto de una fuerza por una distancia su unidad de medida será: T= f . d =1 Newton. 1metro =N. m. C.G.S: El torque estera dado por: T= f. d = 1 Dina. 1centímetro = d.cm. SEGUNDA CONDICION: EQUILIBRIO DE ROTACIÓN Si a un cuerpo que puede girar alrededor de un eje, se la aplican varias fuerzas y no producen variación en su movimiento de rotación, se dice que el cuerpo puede estar en reposo o tener movimiento uniforme de rotación. También se puede decir que un cuerpo se encuentra en equilibrio de rotación si la suma algebraica de los momentos o torques de las fuerzas aplicadas al cuerpo, respecto a un punto cualquiera debe ser igual a cero. Esto es ∑ T= 0 o ∑ M = 0 Una viga de 3 metros de largo tiene un peso de 200N en un extremo y 80N en el extremo opuesto. El peso de la viga es despreciable. Encontrar el punto de equilibrio de la viga. PROBLEMA Si la barra homogénea de 4 Kg de masa se encuentra en equilibrio en la forma que se indica. Determinar la tensión de la cuerda vertical (considerar: g = 10 m/s2). RESOLUCION Hagamos DCL de la barra teniendo presente que la fuerza de reacción en el extremo O debe tener una dirección vertical, porque las otras dos fuerzas que actúan sobre el cuerpo son verticales. Asumiendo que la longitud de la barra es 2L, apliquemos la segunda condición de equilibrio tomando momentos respecto del punto O: = Debes encontrar un punto x tal que la magnitud de ambos momentos ( ya que son en sentidos de giro opuestos ) sean iguales. 200 x = ( 3 - x ) 80 Simplificando da 280 x = 240 x = 6 / 7, entonces x = 0,86 Nm. Y estaría más cerca del peso de 200 N Un cuerpo se encuentra en equilibrio de rotación si el momento resultante de todas las fuerzas que actúan sobre él, respecto de cualquier punto, es nula. . PROBLEMA Si la masa de la barra mostrada es de 3 Kg determinar el módulo de la tensión de la cuerda horizontal y de la reacción en el pasador (considerar g = 10 m/s 2). RESOLUCION Hagamos DCL de la barra, teniendo presente que las tres fuerzas deben ser concurrentes, y apliquemos la segunda condición de equilibrio tomando momentos respecto del punto O. 3. Un automóvil de 2000 kg tiene ruedas de 80cm de diámetro. Se acelera partiendo de reposo hasta adquirir una velocidad de 12m/s en 4 seg. Calcular: cesaria y El torque que aplica a cada una de las ruedas motrices para suministrar esta fuerza. 4 Calcula el valor de la masa (m) y el de x para que las balanzas mostradas en la figura se encuentren en equilibrio. Como la fuerza de gravedad de la barra actúa en su punto medio, se demuestra, por la propiedad de la base media que d = 4 m. A partir de este momento existen dos maneras de llegar a la solución de este problema. La primera forma consiste en aplicar la segunda condición de equilibrio, respecto del punto O, determinar el valor de la tensión T y finalmente construir el triángulo de fuerzas. = Del triángulo de fuerzas mostrado se deduce, aplicando el teorema de Pitágoras, que R = 50 N. ACTIVIDAD 1. Un cuerpo de 15 kg cuelga en reposo arrollado en torno a un cilindro de 12 cm de diámetro. Calcular el torque respecto al eje del cilindro. 2. La barra homogénea mostrada en la figura puede rotar alrededor de O. Sobre la barra se aplican las fuerzas F1 = 5 d , F2 = 8 d y F3= 12 d, si se sabe que OA = 10 cm, OB = 4 cm y OC = 2 cm.. Entonces: el valor del torque resultante que actúa sobre el cuerpo. 5. El brazo mostrado en la figura sostiene un cuerpo masa m Si se encuentra en equilibrio, calcular el torque alrededor de la muñeca, el coco y el hombro cuando una persona sostiene con el brazo extendido el peso correspondiente: