TEMA 3 DA2

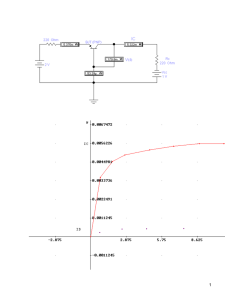
Diseño Análogo 2 – Tema # 3
Capacitancia de unión colector –base 𝑪𝝁
Respuesta en Frecuencia del BJT y el modelo de
alta frecuencia
Esto sucede al tener la polarización inversa en esta
juntura se genera una región de agotamiento que
almacena carga esta viene dada por la ecuación
Hasta el momento se ha supuesto que el transistor
responde de manera instantánea, es decir no se ha
trabajado en los modelos con elementos que
generen una dependencia del tiempo o de
frecuencia. Sin embargo los transistores reales
exhiben fenómenos de almacenamiento de carga
que limitan la velocidad y la frecuencia de
operación, como se vio en la unión pn. A
continuación se hablará de estas capacitancias que
modelaran ese comportamiento.
Capacitancias internas del BJT
𝐶𝜇 =
𝐶𝜇0
𝑚
𝑉
(1+ 𝐶𝐵 )
𝑉𝑂𝐶
Donde 𝐶𝜇0 es el valor de 𝐶𝜇 a voltaje 0, 𝑉𝑂𝐶 =
0.75 y m está entre 0.2 y 0.5
Con esto tenemos que entre las junturas existirán
las siguientes capacitancias
𝐶𝜋 = 𝐶𝑑𝑒 + 𝐶𝑗𝑒 = (Capacitancia Emisor-Base)
𝐶𝜇 (Capacitancia Colector-Base)
Capacitancia de difusión de pequeña señal 𝐶𝑑𝑒 ,
esta es debida a los portadores minoritarios de la
base que generan una carga igual a
𝑊2
𝑄𝑛 = 2𝐷 𝑖𝑐 = 𝜏𝐹 𝑖𝑐
𝑛
Con estos nuevos parámetros se puede modificar
el modelo de pequeña señal anteriormente visto
para tener en cuenta estas capacitancias y hacer un
análisis global del circuito. Este modelo se muestra
en la figura 3.1
Donde
𝑊2
𝜏𝐹 = 2𝐷
𝑛
𝜏𝐹 Se le conoce como tiempo de transito de base
directo y es el tiempo que demora un electrón en
cruzar la base, este valor esta en el intervalo de 10
a 100ps
𝑑𝑄
𝑑𝑖
𝐼
𝐶𝑑𝑒 = 𝑑𝑣 𝑛 = 𝜏𝐹 𝑑𝑣 𝐶 = 𝜏𝐹 𝑔𝑚 = 𝜏𝐹 𝑉𝐶
𝐵𝐸
𝐵𝐸
𝑇
Capacitancia de unión base-emisor 𝑪𝒋𝒆 , ésta es la
capacitancia de la capa de agotamiento y del
estudio del diodo podemos expresar
𝐶𝑗𝑒 =
𝐶𝑗𝑒0
Figura 3.1
Por lo general las hojas de datos no especifican el
valor de 𝐶𝜋 sino el comportamiento de 𝛽 (ℎ𝑓𝑒 ) en
función de la frecuencia y a partir de éste
encontrar los valores de estas capacitancias, para
tal caso debemos estudiar el circuito de la figura
3.2
𝑚
𝑉
(1− 𝐵𝐸 )
𝑉𝑂𝑒
Donde 𝐶𝑗𝑒0 es el valor de 𝐶𝑗𝑒 a voltaje 0, 𝑉𝑂𝑒 es el
voltaje integrado de unión base-emisor = 0.9V y m
= 0.5 aunque es más utilizada pues es más cercano
al comportamiento real
Figura 3.2
𝐶𝑗𝑒 = 2𝐶𝑗𝑒0
𝐼𝐶 = (𝑔𝑚 − 𝑠𝐶𝜇 )𝑉𝜋
1
𝑉𝜋 = 𝐼𝑏 (𝑟𝜋 ‖𝐶𝜋 ‖𝐶𝜇 ) =
𝐼
ℎ𝑓𝑒 = 𝐼𝑐 =
𝑏
𝐼𝑏
1
+𝑠𝐶𝜋 +𝑠𝐶𝜇
𝑟𝜋
Respuesta en frecuencia del amplificador emisor
común
(𝑔𝑚 −𝑠𝐶𝜇 )𝑉𝜋
1
( +𝑠𝐶𝜋 +𝑠𝐶𝜇 )𝑉𝜋
𝑟𝜋
Como a las frecuencias para las que este modelo es
valido 𝑔𝑚 ≫ 𝜔𝐶𝜇 , por tanto se puede ignorar, en
términos de 𝑠𝐶𝜇
ℎ𝑓𝑒 =
𝐼𝑐
𝑔𝑚 𝑟𝜋
𝛽0
=
=
𝐼𝑏 1 + 𝑠(𝐶𝜋 + 𝐶𝜇 )𝑟𝜋 1 + 𝑠(𝐶𝜋 + 𝐶𝜇 )𝑟𝜋
Teniendo así el siguiente diagrama de bode, en
donde 𝜔 𝑇 es la frecuencia a la cual el |ℎ𝑓𝑒 | cae a la
unidad. Y 𝜔𝛽 donde se atenúa 3db del 𝛽0,
Figura 3.3
Figura 3.2
1
𝜔𝛽 = (𝐶
𝜋 +𝐶𝜇 )𝑟𝜋
Para encontrar 𝜔 𝑇 debemos igualar la magnitud
del ℎ𝑓𝑒 a la unidad.
1=|1+𝑗𝜔
𝜔𝑇 2 =
𝛽0
𝑇 (𝐶𝜋 +𝐶𝜇 )𝑟𝜋
|=
𝛽0 2 −1
((𝐶𝜋 +𝐶𝜇 )𝑟𝜋 )
𝜔 𝑇 ≈ (𝐶
𝛽0
𝜋 +𝐶𝜇 )𝑟𝜋
2
≈
𝛽0
√1+(𝜔𝑇 (𝐶𝜋 +𝐶𝜇 )𝑟𝜋 )
𝛽0 2
((𝐶𝜋 +𝐶𝜇 )𝑟𝜋 )
= 𝛽0 𝜔𝛽 = (𝐶
2
2
𝑔𝑚
𝜋 +𝐶𝜇 )
𝑔
𝑓𝑇 = 2𝜋(𝐶 𝑚+𝐶
𝜋
En la figura 3.4 se muestra las 3 bandas en las
cuales se puede dividir la respuesta en frecuencia
de un amplificador. Se puede ver que en la banda
baja, hay disminución de la ganancia debido a los
capacitores 𝐶𝐶1 , 𝐶𝐶2 y 𝐶𝐸 , esto a causa de que a
bajas frecuencias los capacitores dejan de
comportarse como un cortocircuito y generan
atenuación, en la siguiente banda (la banda media)
los capacitores antes mencionados ya no tienen un
efecto significativo y en la última banda las
capacitancias internas del BJT el
𝐶𝜋 y 𝐶𝜇
comienzan a ser significativas y ya no son circuitos
abiertos por lo tanto generan atenuación.
𝜇)
𝑓𝑇 Si es un valor que dan las hojas de datos de allí
podemos encontrar 𝐶𝜋 + 𝐶𝜇 , además es bueno
aclarar que el modelo de la figura 3.1 opera
bastante bien para frecuencias menores a 0.2𝑓𝑇 .
Figura 3.4
Del diagrama se ve que el intervalo de operación
del amplificador es la banda media a este intervalo
se le conoce como ancho de banda
𝐵𝑊 = 𝑓𝐻 − 𝑓𝐿
2
En estas frecuencias la ganancia 𝐴𝑀 o ganancia de
banda media se ha reducido 3dB en donde:
𝐴𝑀 = 𝑣
𝑣0
𝑠𝑒ñ𝑎𝑙
=
𝑅 ‖𝑟𝜋
− (𝑅 ‖𝑟𝐵 )+𝑅
𝑔𝑚 (𝑟0 ‖𝑅𝑐 ‖𝑅𝐿 )
𝐵 𝜋
𝑠𝑒ñ
En los amplificadores el ancho de banda no es
constante, lo que es constante es la relación
ganancia con ancho de banda
𝐺𝐵 = |𝐴𝑀 |𝐵𝑊
𝑣𝑜 = −𝑔𝑚 𝑅 ′ 𝐿 𝑉𝜋
𝐼𝜇 =
𝑉𝜋 −𝑣𝑜
𝑍𝐶𝜇
= 𝑠𝐶𝜇 [𝑉𝜋 − (−𝑔𝑚 𝑅′ 𝐿 𝑉𝜋 )] = 𝑠𝐶𝜇 (1 + 𝑔𝑚 𝑅′ 𝐿 )𝑉𝜋
Siendo esto así podemos remplazar este capacitor
por otro que vaya entre 𝑉𝜋 y tierra y genere la
misma corriente como se muestra en la figura 3.7.
𝑉𝜋
𝑍𝐶𝑒𝑞 =
𝑉𝜋
′
𝜇 (1+𝑔𝑚 𝑅 𝐿 )𝑉𝜋
= 𝑠𝐶
𝐼𝜇
1
Respuesta en alta frecuencia
1
𝑍𝐶𝑒𝑞 = 𝑠𝐶 → 𝐶𝑒𝑞 = 𝑠𝑍
𝑒𝑞
Para el análisis en alta frecuencia los capacitores
𝐶𝐶1 , 𝐶𝐶2 y 𝐶𝐸 se comportan como corto circuitos
entonces obtenemos el modelo que muestra la
figura 3.5.
𝐶𝑒𝑞 = 𝐶𝜇 (1 + 𝑔𝑚 𝑅 ′ 𝐿 )
Figura 3.5
Figura 3.7
Se pueden hacer operaciones circuítales y
simplificar el circuito al mostrado en la figura 3.6
=
𝐶𝑒𝑞
′
𝐿
′
= −𝑔𝑚 𝑅 𝐿 (
1
𝑣𝑂 = −𝑔𝑚 𝑅 ′ 𝐿 (1+𝑠(𝑅′
𝑣𝑂
𝑉𝑠𝑖𝑔
𝑣𝑂
𝑉 ′ 𝑠𝑖𝑔 = 𝑉𝑠𝑖𝑔 𝑅
𝑉𝑠𝑖𝑔
𝑅𝐵
𝑟𝜋
𝐵 +𝑅𝑠𝑖𝑔 𝑟𝜋 +𝑟𝑥 +(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )
𝑅 ′ 𝑠𝑖𝑔 = 𝑟𝜋 ‖[𝑟𝑥 + (𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )]
𝑅
′
𝐿
𝑠
𝑠𝐶𝜇 (1+𝑔𝑚 𝑅′ 𝐿 )
𝐶𝑖𝑛 = 𝐶𝜋 + 𝐶𝜇 (1 + 𝑔𝑚 𝑅 ′ 𝐿 )
𝑣𝑂 = −𝑔𝑚 𝑉𝜋 𝑅
Figura 3.6
1
= −𝑅
𝑓𝐻 =
) 𝑉 ′ 𝑠𝑖𝑔
) 𝑉 ′ 𝑠𝑖𝑔
𝑟𝜋 𝑔𝑚 𝑅 ′ 𝐿
1
(
)
′
𝐵 +𝑅𝑠𝑖𝑔 𝑟𝜋 +𝑟𝑥 +(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 ) 1+𝑠(𝑅 𝑠𝑖𝑔 𝐶𝑖𝑛 )
𝑅𝐵
𝐴
= − (1+𝑠(𝑅′𝑀
𝑠𝑖𝑔 𝐶𝑖𝑛 )
𝜔𝐻 =
𝑠𝑖𝑔 𝐶𝑖𝑛 )
1
𝑠𝐶𝑖𝑛
1
+𝑅 ′ 𝑠𝑖𝑔
𝑠𝐶𝑖𝑛
)
1
′
𝑅 𝑠𝑖𝑔 𝐶𝑖𝑛
1
′
2𝜋(𝑅 𝑠𝑖𝑔 𝐶𝑖𝑛 )
= (𝑟𝑜 ‖𝑅𝐶 ‖𝑅𝐿 )
Del circuito se puede observar que 𝑣𝑜 =
(−𝑔𝑚 𝑉𝜋 + 𝐼𝜇 )𝑅 ′ 𝐿 . Para hacer otra reducción se
puede suponer que para las frecuencias cercanas a
𝑓𝐻 , 𝐼𝜇 es muy pequeña en relación a 𝑔𝑚 𝑉𝜋 por lo
tanto
3
Ejemplo 5.18 pág. 496
Se requiere determinar la ganancia en banda media y la
frecuencia 𝑓𝐻 del amplificador de emisor común, para el
caso siguiente 𝑉𝐶𝐶 = 𝑉𝐸𝐸 = 10𝑉, 𝐼 = 1𝑚𝐴, 𝑅𝑠𝑖𝑔 =
5𝐾Ω, 𝑅𝐵 = 100𝐾Ω , 𝑅𝐶 = 8𝐾Ω , 𝑅𝐿 = 5𝐾Ω, 𝛽0 = 100,
𝑉𝐴 = 100𝑉, 𝐶𝜇 = 1𝑝𝐹 , 𝑓𝑇 = 800𝑀𝐻𝑧 y 𝑟𝑥 = 50Ω.
𝐼
considerar 𝐶𝐸 , se supone que 𝐶𝐶1 y 𝐶𝐶2 son
cortocircuitos perfectos, etcétera.
Efecto de 𝑪𝑪𝟏
1𝑚𝐴
𝑔𝑚 = 𝑉𝐶 = 25𝑚𝑉 = 40 𝑚𝐴⁄𝑉
𝑇
𝑟𝜋 =
𝛽0
𝑔𝑚
=
100
40𝑚𝐴⁄𝑉
𝑟𝑜 =
𝑉𝐴
𝐼𝐶
=
100𝑉
1𝑚𝐴
= 100𝐾
𝑔𝑚
𝐶𝜋 + 𝐶𝜇 =
= 2.5𝐾Ω
2𝜋𝑓𝑇
=
Figura 3.8
40𝑚𝐴⁄𝑉
2𝜋𝑥800𝑥106
En la figura 3.8 se puede apreciar utilizando el
modelo 𝜋 que:
= 8𝑝𝐹
𝐶𝜋 = 8𝑝𝐹 − 1𝑝𝐹 = 7𝑝𝐹
𝐴𝑀 = 𝑣
𝑣0
𝑠𝑒ñ𝑎𝑙
𝑅𝐵 ‖𝑟𝜋 =
= − (𝑅
100𝐾∗2.5𝐾
102.5𝐾
𝑉𝜋 = 𝑉𝑠𝑖𝑔
𝑅𝐵 ‖𝑟𝜋
𝑔𝑚 (𝑟0 ‖𝑅𝑐 ‖𝑅𝐿 )
𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ
𝑉𝑜
𝑉𝑠𝑖𝑔
1
1
1
1
+ +
100𝑘 8𝐾 5𝐾
= 2.985𝐾
2.44𝐾
𝑉𝑜
𝑉𝑠𝑖𝑔
𝑉
𝐴𝑀 = 2.44𝐾+5𝐾 0.040(2.985𝐾) = −39 𝑉
𝑉𝑜
𝐶𝑖𝑛 = 𝐶𝜋 + 𝐶𝜇 (1 + 𝑔𝑚 𝑅′ 𝐿 ) = 7𝑝𝐹 + 1𝑝𝐹(1 + 40(2.985))
𝑉𝑠𝑖𝑔
𝐶𝑖𝑛 = 128𝑝𝐹
𝑅 ′ 𝑠𝑖𝑔 = 𝑟𝜋 ‖[𝑟𝑥 + (𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )] = 2.5𝐾 ‖[50 +
𝑅 ′ 𝑠𝑖𝑔 =
𝑓𝐻 =
2.5𝐾∗4.8𝐾
7.3𝐾
1
2𝜋(𝑅′ 𝑠𝑖𝑔 𝐶𝑖𝑛 )
(𝑅𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ +
1
𝑠𝐶𝐶1
𝑉𝑜 = −𝑔𝑚 (𝑅𝑐 ‖𝑅𝐿 )𝑉𝜋
= 2.44𝐾
𝑅 ′ 𝐿 = 𝑟0 ‖𝑅𝑐 ‖𝑅𝐿 =
𝑅𝐵 ‖𝑟𝜋
𝑉𝑜
5∗100
( 105 )]
𝑉𝑠𝑖𝑔
= −𝑔𝑚 (𝑅𝑐 ‖𝑅𝐿 )
1
𝑠𝐶𝐶1
𝑠𝐶𝐶1 (𝑅𝐵 ‖𝑟𝜋 )
)
𝐶1 [(𝑅𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ ]+1
= −𝑔𝑚 (𝑅𝑐 ‖𝑅𝐿 ) (𝑠𝐶
= −𝑔𝑚 (𝑅𝑐 ‖𝑅𝐿 ) (
𝐶𝐶1 (𝑅𝐵 ‖𝑟𝜋 )
𝐶𝐶1 [(𝑅𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ ]
1
𝑠+
𝐶𝐶1[(𝑅𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ ]
𝑠
(𝑅𝐵 ‖𝑟𝜋 )
𝑔𝑚 (𝑅𝑐 ‖𝑅𝐿 ) (
𝑠+
𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ
= − (𝑅
𝜔𝑝1 =
= 1.65𝐾
𝑅𝐵 ‖𝑟𝜋
(𝑅𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ +
)
𝑠
1
𝐶𝐶1 [(𝑅𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ ]
)
1
𝐶𝐶1 [(𝑅𝐵 ‖𝑟𝜋 )+𝑅𝑠𝑒ñ ]
Efecto de 𝑪𝑬
1
= 2𝜋(1.65𝐾∗128𝑝) = 754𝐾𝐻𝑧
Respuesta en baja frecuencia
Para determinar la ganancia de baja frecuencia se
remplaza el transistor por el modelo π, en este caso las
capacitancias internas del transistor no tendrán efecto y
por lo tanto no se tendrán en cuenta, también para
facilitar el análisis no se tendrá en cuenta ni 𝑟0 ni 𝑟𝑥
debido a que no tienen mucho efecto. Además para
hacer el análisis se considerará el efecto de los tres
condensadores por separado, es decir cuando se
determina el efecto de 𝐶𝐶1 , se supone que 𝐶𝐶2 y 𝐶𝐸
actúan
como
cortocircuitos
perfectos
y
al
Figura 3.9
En la figura 3.9 se puede deducir utilizando el
modelo T que:
4
𝐼𝑏 = (𝑅
𝑅𝐵
1
𝑉𝑠𝑖𝑔 )
1
+𝑅
𝐵
𝑠𝑖𝑔
(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )+(𝛽+1)(𝑟𝑒 +
)
Ahora que se determinaron los efectos de cada uno
de los capacitores por separado podemos decir que
la respuesta en frecuencia se aproxima a
𝑠𝐶𝐸
𝑉𝑜 = −𝐼𝑐 (𝑅𝑐 ‖𝑅𝐿 ) = −𝛽𝐼𝑏 (𝑅𝑐 ‖𝑅𝐿 )
𝑉𝑜
𝑉𝑠𝑖𝑔
𝑉𝑜
𝑉𝑠𝑖𝑔
𝑉𝑜
=
𝑅
−𝛽(𝑅𝑐 ‖𝑅𝐿 ) (𝑅 +𝑅𝐵 )
𝐵
𝑠𝑖𝑔 (𝑅
1
=
𝑅
𝑠𝐶 𝛽(𝑅𝑐 ‖𝑅𝐿 )
− (𝑅 +𝑅𝐵 ) (𝑅 ‖𝑅 )𝑠𝐶𝐸 +(𝛽+1
)(𝑠𝐶𝐸 𝑟𝑒 +1)
𝐵
𝑠𝑖𝑔
𝑠𝑖𝑔 𝐵
𝐸
=
[(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )+(𝛽+1)𝑟𝑒 ]𝐶𝐸
𝑅
− (𝑅 +𝑅𝐵 )
(𝛽+1)
𝐵
𝑠𝑖𝑔 𝑠+
1
𝑠𝑖𝑔 ‖𝑅𝐵 )+(𝛽+1)(𝑟𝑒 +𝑠𝐶 )
𝐸
𝑉𝑠𝑖𝑔
𝑉𝑜
𝑉𝑠𝑖𝑔
[(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )+(𝛽+1)𝑟𝑒 ]𝐶𝐸
=
𝑅
𝛽(𝑅 ‖𝑅𝐿 )
− (𝑅 +𝑅𝐵 ) [(𝑅 ‖𝑅 )𝑐+(𝛽+1
)𝑟𝑒 ] 𝑠+
𝐵
𝑠𝑖𝑔
𝑠𝑖𝑔 𝐵
𝑠
𝑝1
𝑝2
𝑝3
En la mayoría de casos la que domina es 𝜔𝑝2 debido
𝜔𝑝𝐿 = 𝜔𝑝2
𝑠
1
(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )
[
+𝑟𝑒 ]𝐶𝐸
(𝛽+1)
𝜔𝑝2 =
𝑠
a que es el capacitor que ve la resistencia más pequeña
en este caso entonces 𝜔𝑝2 será la frecuencia de corte a
la hora de diseñar a esta se le asigna un valor del 80% o
más de la frecuencia a la cual se desea que atenue y a
las demás el porcentaje restante.
𝑠𝐶𝐸 𝛽(𝑅𝑐 ‖𝑅𝐿 )
𝑉𝑜
𝑉𝑠𝑖𝑔
𝑠
= −𝐴𝑀 (𝑠+𝜔 ) (𝑠+𝜔 ) (𝑠+𝜔 )
1
(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )
[ (𝛽+1) +𝑟𝑒 ]𝐶𝐸
Si por alguna razón los 3 capacitores contribuyen de
manera significativa a la frecuencia de corte es decir
están muy cerca ambas frecuencias entonces la
frecuencia de corte resultante es la suma de las tres
𝜔𝑝𝐿 = 𝜔𝑝1 + 𝜔𝑝2 + 𝜔𝑝3
Efecto de 𝑪𝑪𝟐
Ejemplo 5.19 pág. 502
Se desea seleccionar valores apropiados para 𝐶𝐶1 , 𝐶𝐶2 y
𝐶𝐸 para el amplificador de emisor común, el
amplificador tiene 𝑅𝑠𝑖𝑔 = 5𝐾Ω, 𝑅𝐵 = 100𝐾Ω , 𝑅𝐶 =
8𝐾Ω , 𝑅𝐿 = 5𝐾Ω, 𝛽0 = 100, 𝑔𝑚 = 40 𝑚𝐴⁄𝑉 y 𝑟𝜋 =
2.5𝐾Ω se requiere tener una 𝑓𝐿 = 100𝐻𝑧.
Se determinan las resistencias que detectan los tres
condensadores 𝐶𝐶1 , 𝐶𝐶2 y 𝐶𝐸
Figura 3.10
En la figura 3.10 se puede apreciar utilizando el
modelo 𝜋 que:
𝑉𝜋 = 𝑉𝑠𝑖𝑔 (𝑅
𝑅𝐵 ‖𝑟𝜋
‖𝑟
𝐵 𝜋 )+𝑅𝑠𝑒ñ
𝑉𝑜 = −𝑔𝑚 𝑉𝜋
𝑉𝑜
𝑉𝑠𝑖𝑔
𝑉𝑜
𝑉𝑠𝑖𝑔
𝑉𝑜
𝑉𝑠𝑖𝑔
𝑅𝑐
1
𝑅𝐶 +
+𝑅𝐿
𝑠𝐶𝐶2
𝑅𝐿
=
𝑅 ‖𝑟𝜋
(𝑅𝐶 +𝑅𝐿 )𝐶𝐶2
−𝑔𝑚 𝑅𝐿 (𝑅 ‖𝑟𝐵 )+𝑅
1
𝐵 𝜋
𝑠𝑒ñ 𝑠+
𝑠𝐶𝐶2 𝑅𝑐
(𝑅𝐶 +𝑅𝐿 )𝐶𝐶2
𝜔𝑝3 =
+ 5𝐾 = 7.44𝐾Ω
0.99
(𝑅𝑠𝑖𝑔 ‖𝑅𝐵 )
(𝛽+1)
+ 𝑟𝑒 =
5𝐾∗100𝐾
105𝐾
101
+ 25 = 72Ω
𝑅𝐶2 = 𝑅𝐶 + 𝑅𝐿 = 8𝐾 + 5𝐾 = 13𝐾Ω
=
𝑅 ‖𝑟𝜋
− (𝑅 ‖𝑟𝐵 )+𝑅
𝑔𝑚 (𝑅𝐿 ‖𝑅𝐶 )
𝑠+
𝐵 𝜋
𝑠𝑒ñ
1
(𝑅𝑐 +𝑅𝐿 )𝐶𝐶2
100𝑘∗2.5𝑘
102.5𝐾
𝑟𝑒 = 0.04 = 25Ω
𝑅𝐸 =
𝑅 ‖𝑟𝜋
𝑠𝐶𝐶2 𝑅𝑐
−𝑔𝑚 𝑅𝐿 (𝑅 ‖𝑟𝐵 )+𝑅
𝐵 𝜋
𝑠𝑒ñ (𝑅𝐶 +𝑅𝐿 )𝐶𝐶2 𝑠+1
=
𝑅𝐶1 = (𝑅𝐵 ‖𝑟𝜋 ) + 𝑅𝑠𝑒ñ =
𝑠
1
(𝑅𝐶 +𝑅𝐿 )𝐶𝐶2
Ahora seleccionamos 𝐶𝐸 de tal modo que contribuya
con el 80% del valor de 𝜔𝐿
1
𝐶𝐸 𝑥72
= 0.8𝑥2𝜋𝑥100
𝐶𝐸 =
1
0.8𝑥2𝜋𝑥100𝑥72
= 27.6𝜇𝐹
𝐶𝐶1 Contribuirá con un 10%
1
𝐶𝐶1 = 0.1𝑥2𝜋𝑥100𝑥7.44𝐾 = 2.1𝜇𝐹
5
Y otro 10% para 𝐶𝐶2
1
𝐶𝐶2 = 0.1𝑥2𝜋𝑥100𝑥13𝐾 = 1.2𝜇𝐹
Donde se tiene
1. En 𝑣𝐼 = 𝑉𝑂𝐿 = 𝑉𝐶𝐸𝑠𝑎𝑡 = 0.2𝑉, 𝑣𝑂 = 𝑉𝑂𝐻 = 𝑉𝐶𝐶 = 5𝑉
En la práctica se deben escoger los valores más
aproximados mientras la 𝑓𝐿 se mantenga por debajo de
100Hz.
2. En 𝑣𝐼 = 𝑉𝐼𝐿 ≅ 0.7𝑉 el transistor comienza a activarse
3. Para entre este valor y 𝑉𝐼𝐿 < 𝑣𝐼 < 𝑉𝐼𝐻 el transistor
opera en la región activa con una ganancia
Inversor lógico Digital
𝐴𝑣 =
Un inversor lógico simple se muestra en la figura 3.11
𝑣𝑂
𝑣𝐼
=𝑖
−𝛽𝑖𝑏 𝑅𝐶
𝑏 (𝑅𝐵 +𝑟𝜋 )
= −𝛽 𝑅
1
𝑉
𝑅𝐶
𝑅
𝐵 +𝑟𝜋
≈ −𝛽 𝑅𝐶
𝐵
= −50 10 = −5 𝑉
4. En 𝑣𝐼 = 𝑉𝐼𝐻 el transistor entra en saturación es
donde para calcularlo se mirar que valor de En 𝑣𝐼 se
requiere para que el transistor opere en la frontera se
calcula la corriente de base en saturación
𝐼𝐵 =
(𝑉𝐶𝐶 −𝑉𝐶𝐸𝑠𝑎𝑡 )⁄𝑅𝐶
𝛽
=
(5−0.2)⁄1𝐾
50
= 96𝜇𝐴
Y luego
Figura 3.11
Este circuito se debe diseñar de tal forma que el
transistor opere en saturación con un voltaje de entrada
alto cercano a VCC esto se hace con una buena elección
de 𝑅𝐵 y 𝑅𝐶 , en donde se sabe que el voltaje de salida
será el 𝑉𝐶𝐸𝑠𝑎𝑡 = 0.2𝑉 que es un voltaje bajo, y cuando
la entrada es 0.2V el transistor estará en corte por lo
tanto no habrá corriente y por ende el voltaje de salida
es VCC, que es un nivel alto. A continuación en la figura
3.12 se muestra la VTC (característica de transferencia
de voltaje) del inversor, supongamos una 𝑅𝐵 = 10𝐾Ω,
𝑅𝐶 = 1𝐾Ω, 𝛽𝑚𝑖𝑛 = 50 y 𝑉𝐶𝐶 = 5𝑉.
𝑉𝐼𝐻 = 𝐼𝐵 𝑅𝐵 + 𝑉𝐵𝐸 = 96𝜇𝐴(10𝐾Ω) + 0.7 = 1.66𝑉
5. Para 𝑣𝐼 = 𝑉𝑂𝐻 = 5𝑉, el transistor estará muy dentro
de la saturación con 𝑣𝑂 = 𝑉𝐶𝐸𝑠𝑎𝑡 = 0.2𝑉 y
𝛽𝑓𝑜𝑟𝑧𝑎𝑑𝑎 =
𝐼𝐶𝑠𝑎𝑡
𝐼𝐵
=
(𝑉𝐶𝐶 −𝑉𝐶𝐸𝑠𝑎𝑡 )⁄𝑅𝐶
(𝑉𝑂𝐻 −𝑉𝐵𝐸 )⁄𝑅𝐵
= 11
Ahora con toda esta información es posible calcular los
márgenes de ruido
𝑁𝑀𝐻 = 𝑉𝑂𝐻 − 𝑉𝐼𝐻 = 5 − 1.66 = 3.34𝑉
𝑁𝑀𝐿 = 𝑉𝐼𝐿 − 𝑉𝑂𝐿 = 0.7 − 0,2 = 0.5𝑉
Como se puede apreciar los márgenes de ruido en
alta y baja son muy distintos, lo ideal es que fuesen
iguales y con un valor muy próximo a 𝑉𝐶𝐶 /2
Figura 3.12
6