Caso 9. Estimar el modelo óptimo que caracteriza la Estimar

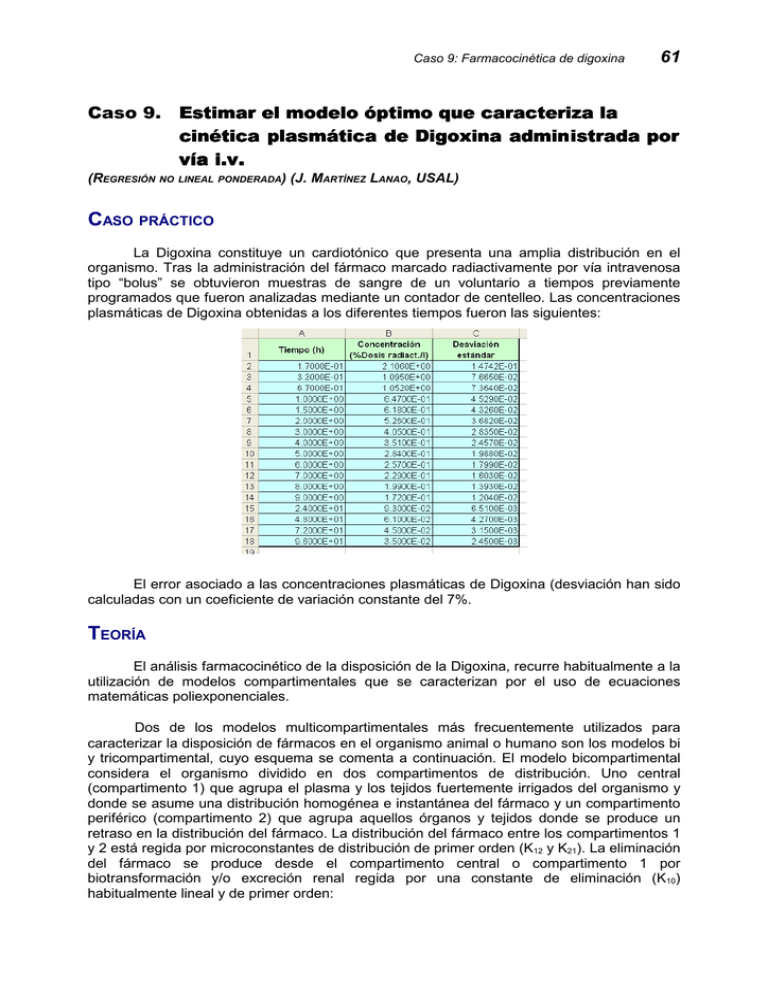
Caso 9: Farmacocinética de digoxina
61
Caso 9. Estimar el modelo óptimo que caracteriza la
cinética plasmática de Digoxina admini
admin istrada por
vía i.v.
i.v.
(REGRESIÓN NO LINEAL PONDERADA) (J. MARTÍNEZ LANAO, USAL)
CASO PRÁCTICO
La Digoxina constituye un cardiotónico que presenta una amplia distribución en el
organismo. Tras la administración del fármaco marcado radiactivamente por vía intravenosa
tipo “bolus” se obtuvieron muestras de sangre de un voluntario a tiempos previamente
programados que fueron analizadas mediante un contador de centelleo. Las concentraciones
plasmáticas de Digoxina obtenidas a los diferentes tiempos fueron las siguientes:
El error asociado a las concentraciones plasmáticas de Digoxina (desviación han sido
calculadas con un coeficiente de variación constante del 7%.
TEORÍA
El análisis farmacocinético de la disposición de la Digoxina, recurre habitualmente a la
utilización de modelos compartimentales que se caracterizan por el uso de ecuaciones
matemáticas poliexponenciales.
Dos de los modelos multicompartimentales más frecuentemente utilizados para
caracterizar la disposición de fármacos en el organismo animal o humano son los modelos bi
y tricompartimental, cuyo esquema se comenta a continuación. El modelo bicompartimental
considera el organismo dividido en dos compartimentos de distribución. Uno central
(compartimento 1) que agrupa el plasma y los tejidos fuertemente irrigados del organismo y
donde se asume una distribución homogénea e instantánea del fármaco y un compartimento
periférico (compartimento 2) que agrupa aquellos órganos y tejidos donde se produce un
retraso en la distribución del fármaco. La distribución del fármaco entre los compartimentos 1
y 2 está regida por microconstantes de distribución de primer orden (K12 y K21). La eliminación
del fármaco se produce desde el compartimento central o compartimento 1 por
biotransformación y/o excreción renal regida por una constante de eliminación (K10)
habitualmente lineal y de primer orden:
62
Caso 9: Farmacocinética de digoxina
K12
A1
A2
K21
K10
Modelo bicompartimental
El modelo tricompartimental se utiliza para fármacos que se caracterizan por
presentar una distribución muy amplia en el organismo. La filosofía de diseño de modelo
tricompartimental es análoga a la del modelo bicompartimental. La diferencia fundamental
estriba en que se asume la existencia de un compartimento central (compartimento 1)
análogo al del modelo anterior y dos compartimentos periféricos, accesible (compartimento 2)
y profundo (compartimento 3) existiendo diferencias en la velocidad de distribución del
fámarco:
K31
A3
K12
A1
A2
K 13
K21
K10
Modelo tricompartimental
Ambos modelos se formulan matemáticamente utilizando ecuaciones diferenciales
ordinarias, lineales y de primer orden. Estos sistemas de ecuaciones convenientemente
integrados, utilizando, entre otros, herramientas matemáticas muy útiles como por ejemplo
las trasnformadas de Laplace, generan ecuaciones poliexponenciales habituales en el campo
de la Farmacocinética. La solución analítica del modelo bicompartimental para un fármaco
que se administra por vía intravenosa tipo “bolus” es la de una ecuación biexponencial
desdendente:
Solución para el compartimento central (1):
A 1 = A(1)e − 1 t + A(2)e − 2 t
Las constantes 1 y 2 son macroconstantes o constantes híbridas que se relacionan
matemáticamente con las microsconstantes del modelo mediante la siguiente ecuación:
1 + 2 = K 12 + K 21 + K 10
La solución analítica del modelo tricompartimental equivalente es la de una ecuación
triexponencial descendente:
Solución para el compartimento central (1):
A 1 = A(1)e − 1 t + A(2)e − 2 t + A(3)e − 3 t
1 + 2 + 3 = K 12 + K 21 + K 13 + K 31 + K 10
Los parámetros de las ecuaciones matemáticas exponenciales pueden estimarse
mediante regresión no-lineal ponderada con la ayuda de SIMFIT. El programa utilizado para
Caso 9: Farmacocinética de digoxina
63
resolver este problema es “EXFIT” localizado en el menú Fit del SIMFIT y que permite ajustar
los parámetros de una ecuación poliexponencial entre 1 y “n” exponenciales.
En este caso concreto utilizaremos EXFIT para ajustar los datos del problema a 2 y 3
exponenciales, que corresponden a los modelos bi y tricompartimentales respectivamente. Al
tratarse de datos con error no constante realizaremos una “regresión no lineal con pesos
estadísticos” o “regresión no lineal ponderada”.
PROCEDIMIENTO PASO A PASO
1.- Abrir el archivo con los datos: caso9.xls.
Abra el archivo, seleccione los datos númericos y cópielos al portapapeles. Se
importarán a Simfit en su momento mediante la opción Paste.
2.- Ajuste de los datos a ecuaciones poliexponenciales.
En la barra de opciones del menú principal despliegue la opción Fit y dentro de ella
seleccione Sum of 1 to n exponentials functions - exfit y Run the program.
A continuación aparece una pantalla con 6 opciones debiendo seleccionarse la opción
1 que corresponde a decaimientos exponenciales:
Ahora deberemos importar los datos de nuestro archivo que los tenemos en el
protapapeles, para ello seleccionamos:
New data > OK > File/Clipboard > Paste > OK > Open.
Una vez cargados los datos procedemos al análisis seleccionando Analyse the
current data set.
64
Caso 9: Farmacocinética de digoxina
Nos pide que introduzcamos el orden inferiror y superior del modelo, en este caso 2 y
3 respectivamente correspondiendo al número de exponenciales que se pretende
optimizar en cada caso.
A continuación se selecciona el método a usar para las estimadas iniciales de los
parámetros. Seleccionamos You input paramenter starting estimates.
Seleccionamos el tipo de salida debiendo marcarse las opciones recogidas en el
cuadro:
Es importante disponer de información sobre la bondad del ajuste así como de la
representación de residuales que serán muy útiles para discriminar entre modelos
farmacocinéticos.
A continuación se introducen las estimadas iniciales para el caso de 2 exponenciales.
En el ejemplo utilizaremos:
A(1)=0.1, A(2)=1, k(1)=0.02, k(2)=0.4
Una vez realizado el ajuste, el programa presenta en la pantalla los parámetros
optimizados. Además de los coeficientes y exponentes de la ecuación exponencial
EXFIT calcula el área bajo la curva de niveles plasmáticos (AUC) entre tiempo 0 e ∞.
El AUC es un parámetro farmacocinético muy utilizado para análisis
modelo-independiente o para cálculos de biodisponibilidad y bioequivalencia.
Caso 9: Farmacocinética de digoxina
65
En esta tabla aparece, junto con el valor óptimo de cada parámetro del modelo
seleccionado, el error estándar del parámetro, así como los límites de confianza al
95% para dicho parámetro. Así mismo, la tabla muestra la probabilidad (p) de que el
parámetro sea redundante, es decir practicamente igual a cero.
A continuación, el programa muestra la matriz de correlación de los parámetros
seguida de la tabla que muestra los datos experimentales junto a los valores teóricos
ajustados. Por último, aparece una tabla con toda la estadística asociada al ajuste.
Posteriormente el programa muestra el gráfico correspondiente al ajuste:
66
Caso 9: Farmacocinética de digoxina
A continuación da la opción de realizar una descomposición llamada Deconvolution
por el programa, que permite analizar la contribución de cada término exponencial en
el proceso global:
Seguidamente el programa reinicia el proceso ahora para un modelo de 3
exponenciales. En este punto habrá que introducir como estimas iniciales las
siguientes:
A(1)=0.1, A(2)=1, A(3)=4, k(1)=0.01, k(2)=0.3, k(3)=8
A continuación aparecerán los parámetros respectivos, la estadística asociada al
ajuste, las gráficas, etc, de manera análoga a lo visto anteriormente para el caso de 2
exponenciales.
Finalmente SIMFIT presenta una tabla en la que se comparan los dos modelos
probados mediante estadísticos relacionados con la bondad del ajuste y la
discriminación entre modelos rivales, como son el test F y los criterios de Akaike (AIC)
y de Schwarz (SC). Allí se podrá de manifiesto que la función con 3 exponenciales
ajusta estadísticamente mejor los datos que la función con 2 exponenciales.
Es interesante durante la realización del ejercicio examinar los gráficos de residuales
frente a las variables independiente (tiempo de obtención de la muestra) y
dependiente (valor predicho de la concentración plasmática). El análisis de residuales
constituye una herramienta muy útil para evaluar la bondad del ajuste y para
discriminar entre modelos rivales.