Dinámica

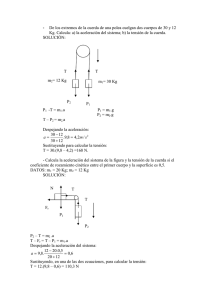
FISICA GENERAL – CURSADA 2015
Trabajo Práctico Nº 2: DINÁMICA
Prof. Olga Garbellini
Dr. Fernando Lanzini
Para resolver problemas de dinámica es muy importante seguir un orden, que podemos resumir
en los siguientes pasos:
1. Hacer un diagrama por separado de los distintos cuerpos que intervienen en el problema
y dibujar las fuerzas que actúan sobre cada uno de ellos. Este diagrama se denomina
Diagrama de Cuerpo Libre (DCL)
2. Expresar la ley de Newton en forma vectorial para cada cuerpo.
3. Elegir un sistema de ejes cartesianos para cada cuerpo. Si es posible, conviene hacer
coincidir uno de ellos con la dirección del vector aceleración y tomar como positivo el
sentido de dicho vector.
4. Proyectar las fuerzas según los ejes elegidos.
5. Aplicar la segunda ley de Newton para cada cuerpo en cada eje, teniendo en cuenta el
criterio de signos. Si hemos seguido la recomendación del paso 3, las fuerzas que vayan en
el sentido de la aceleración serán positivas y las opuestas negativas.
6. Resolver el sistema de ecuaciones.
7. Comprobar que el resultado tiene sentido: órdenes de magnitud, signos de las magnitudes,
etc.
2.1. Una fuerza F = (6i-3j) actúa sobre una masa de 2 kg. Halle la aceleración a. ¿Cuál es el
módulo de a? (Rta: a = (3i-1.5j); | a | = 3.35 m/s2)
2.2. ¿Cuál es el momentum lineal de un camión cuya masa es 10 toneladas y se mueve a 20
m/s? ¿Qué velocidad debe alcanzar un auto de 1 tonelada para tener el mismo momentum
lineal? (Rtas: p = 200000 kg·m/s; v’=200 m/s)
2.3. Halle el momentum lineal adquirido por cada una de las siguientes masas: 1g, 1 kg y 1000
kg, cuando cada una de ellas cae una distancia de 100 m. (Rtas: 0.0447, 44.7, y 44700 kg·m/s)
2.4. Para cada una de las siguientes situaciones dibuje el diagrama de cuerpo libre (DCL) y
calcule la normal para cada caso.
2.5. Un ascensor de 400 kg de masa (considerando la carga)
a) sube con velocidad constante,
b) acelera hacia arriba a razón de 2m/s2,
c) acelera hacia abajo a razón de 2 m/s2,
d) cae libremente.
Calcule la tensión del cable en todos los casos.
(Rtas: (a) T = 4000 N; (b) T = 4800 N; (c) T = 3200 N; (d) T = 0)
2.6. Dos bloques están en contacto sobre una mesa como muestra la figura. Si se le aplica una
fuerza constante: 1) horizontal y 2) formando un ángulo de 30° con la horizontal, despreciando
el rozamiento calcular:
F
a) La aceleración que adquiere el sistema en cada caso.
m1
m2
b) La fuerza de interacción entre ambos cuerpos.
DATOS: F= 20 N; m1 = 2 kg y m2 = 3 kg,
(Rtas: 1) a) 4 m/s2; b) 12 N; 2) a) 3.46 m/s2; b) 10.39 N)
2.7. Dos cuerpos A y B de 2Kg y 6Kg de masa, suben verticalmente con movimiento acelerado
bajo la acción de una fuerza F de 120N de intensidad. Calcular la fuerza de contacto entre A y
B.
(Rta: 30 N)
2.8. Se acelera un bloque de 6Kg sobre una superficie horizontal rugosa mediante una fuerza de
40N que actúa hacia abajo a un ángulo de 37° por debajo de la horizontal. Una fuerza de
fricción de 20N actúa en la superficie de contacto entre el bloque y el plano. Hallar: la
aceleración del bloque y el coeficiente de fricción entre el bloque y el plano.
(Rtas: a = 1.99 m/s2; µ = 0.238)
2.9. Si quisieras acostarte en una hamaca paraguaya cuyas cuerdas de suspensión están
desgastadas ¿qué es mejor, colgarla de dos árboles cercanos o distantes?
2.10. Se conectan dos masas de 3 kg y 5 kg por medio de
una cuerda ligera que pasa sobre una polea lisa, como se
indica en la figura. Determine a) la tensión en la cuerda b)
la aceleración de cada masa y c) la distancia que recorre
cada masa en el primer segundo del movimiento, si parten
del reposo. (Rtas: T = 37.5 N; a = 2.5 m/s2; d = 1.25 m)
2.11. Un bloque B cuelga de una cuerda de masa despreciable que pasa por una polea sin
rozamiento, y ésta conectada a otros dos bloques A y C unidos por una cuerda que se encuentran
sobre una mesa. Encontrar la aceleración de los bloques y las tensiones de las cuerdas. El
coeficiente de rozamiento dinámico entre el bloque A y la superficie es de 0.25 y el bloque C y
la superficie es de 0.30. mA= 0.60 Kg. ; mB= 0.8Kg y mC=0.1Kg.
2.12. En la Figura el coeficiente de roce entre los bloques
de masa m2 y m3 es 0.3 y entre m3 y la mesa es 0.2. Si
m1=15 Kg m2=3Kg y m3=4Kg. Determinar: la aceleración
del sistema y las tensiones de las cuerdas.
2.13. Halle la aceleración de un esquiador que se desliza por la ladera de una colina inclinada
30° con la horizontal, con rozamiento despreciable. ¿Cuál será la inclinación de la pista, cuando
su aceleración sea 8 m/s2 ?.
2.14. Un bloque de 4 kg asciende a lo largo de un plano inclinado 30º, cuando se le aplica una
fuerza F que forma 15º con la horizontal, tal como se indica en la figura. Sabiendo que el
bloque, parte del reposo, en la base del plano inclinado, y alcanza una velocidad de 6 m/s
después de recorrer 10 m a lo largo del plano y que el coeficiente de rozamiento entre el cuerpo
y el plano inclinado es 0.2.
a) Determinar el valor de la fuerza F.
b) En dicha posición, x=10 m, se deja de aplicar la fuerza F. Determinar el desplazamiento total
del móvil a lo largo del plano hasta que se para.
2.15. Un bloque de 20 kg está inicialmente en reposo sobre una superficie horizontal rugosa. Se
requiere una fuerza horizontal de 75 N para hacer que el bloque se ponga en movimiento. Una
vez que se encuentra en movimiento, se requiere una fuerza horizontal de 60 N para mantenerlo
en movimiento con velocidad constante. Calcule los coeficientes de rozamiento estático y
cinético, a partir de esta información.
2.16. Los tres bloques de la figura están conectados por medio de cuerdas ligeras que pasan
sobre poleas sin fricción. La aceleración del sistema es de 2 m/s2 y las superficies son rugosas.
Calcule a) las tensiones en las cuerdas y b) el coeficiente de rozamiento cinético entre los
bloques y las superficies. (Suponga el mismo para ambos bloques.)
2.17. (a) Un cuerpo de 25Kg se desliza en un plano inclinado α= 30°, y está unida mediante una
cuerda que pasa por una polea, a otro cuerpo suspendido libremente de 40Kg. Hallar: la
aceleración del sistema, suponiendo que el µk=0.2. (b) Determine la aceleración con que se
moverán los cuerpos de la figura y la tensión de la cuerda cuando hay fricción, siendo µ1= 0.12
en la superficie donde está apoyada m1 y µ2= 0.10 en la superficie donde está apoyada m2.
Explique todos los movimientos posibles. Datos: m1= 20 kg, m2= 18 kg, α= 30°, β= 60°.
2.18. En el sistema de la figura la masa m2 está apoyada sin rozamiento sobre un plano
inclinado un ángulo α y entre la masa m1 y el plano horizontal el coeficiente de rozamiento
cinético es μk. Las dos masas están unidas entre sí por una cuerda inextensible y de masa
despreciable que pasa por una polea sin masa. Sobre m1 se aplica una F = 20 N de modo que el
resorte
de
constante
recuperadora
K
sufre
una
deformación
x.
o
2
Datos: m1 = 2 kg; m2 = 0.5 kg; μk = 0.2; α= 30 ; K = 150 N/m . Tomar g = 10 m/s2
a) Hacer un DCL de m1 y dibujar las fuerzas que actúan sobre él. Hacer lo mismo para m2. b)
Calcular la aceleración de los bloques y la tensión en la cuerda en el instante en que el resorte se
ha estirado una longitud x = 0.03 m con respecto a su posición de equilibrio.
2.19. Se aprieta un borrador contra un pizarrón como indica la figura.
¿Cuál es la fuerza que hay que aplicarle para que no se caiga siendo el μe =
0,4?
2.20. Se observa que el sistema descrito en la figura tiene
una aceleración de 1.5 m/s2, cuando los planos inclinados
son ásperos. Suponga que los coeficientes de rozamiento
cinético entre cada bloque y los planos inclinados son los
mismos. Halle a) el coeficiente de rozamiento cinético y b)
la tensión en la cuerda.
2.21. El cuerpo 1 gira sobre una mesa horizontal con rozamiento despreciable, mantenido por
una cuerda que pasa por un orificio en su centro, de la que cuelga el cuerpo 2.
a- Si ambos cuerpos tienen masas iguales, hallar la
frecuencia con que el cuerpo 1 describe una circunferencia
de 0,4 m de radio.
b- Hallar el nuevo radio para duplicar la frecuencia anterior
sin cambiar los cuerpos.
2. 22. Un bloque de 1 kg de masa está atado a una cuerda de 0.6 m de largo y gira a 60 rpm en
un círculo vertical. Calcule
a) la tensión en la cuerda cuando el bloque está en el punto más alto del círculo, en el más bajo
y cuando la cuerda está horizontal.
b) la velocidad lineal y angular que debe tener el bloque en el punto más alto para que la
tensión en la cuerda sea cero.
2. 23. Con la ayuda de una cuerda se hace girar un cuerpo de 1Kg en una circunferencia de 1m
de radio en un plano vertical, cuyo centro está situado a 6m por encima del suelo. La cuerda se
rompe cuando la tensión es de 100N, lo cual ocurre cuando el cuerpo está en el punto mas bajo
de la trayectoria. Calcular:
a)
Velocidad del cuerpo cuando se rompe la cuerda.
b)
¿Cuánto tiempo tardará en caer al suelo?
c)
¿Cuál será la velocidad en el instante de chocar con el suelo?
2.24. En un parque de atracciones, los participantes se sostienen contra las paredes de un
cilindro giratorio mantenidos por la fuerza de rozamiento. Si el coeficiente de roce estático entre
los participantes y la pared vale 0.4 y el radio del cilindro es de 5m, hallar la frecuencia mínima
necesaria en rpm para no deslizarse. Si su altura sobre el suelo es de 3m, cuánto tardarán en
caerse si por error la frecuencia es de 20 rpm? (considere µk= 0.3).
+
2.25. El vector posición de un cuerpo de 6 kg de masa está dado por: = 3 − 6
−4
m. Halle:
a) la fuerza que actúa sobre la partícula,
b) el torque con respecto al origen que actúa sobre la partícula, y
c) los momentum lineal y angular de la partícula con respecto al origen.
2.26. Una cuerda se enrolla alrededor de un cilindro de 3 kg y radio de 10 cm que es libre de
girar alrededor de su eje. Se tira de la cuerda con una fuerza de 15 N. El cilindro está
inicialmente en reposo cuando t=0. Halle:
a) el torque ejercido por la cuerda y la aceleración angular del cilindro,
b) la velocidad angular del cilindro para t 0 4 s.
2.27. Un cuerpo de 3 kg se mueve a velocidad constante de 4 m/s a lo largo de una línea recta.
Cuál es su momentum angular respecto de un punto situado a 5 m de la línea? Describa
cualitativamente como varía con el tiempo su velocidad angular respecto a dicho punto.
2.28. Una partícula de 2 kg se mueve en una circunferencia de radio 3 m. Su momentum angular
respecto al centro de la misma depende del tiempo de acuerdo con la expresión L = 4 (N.m)t.
Halle
a)
el torque de la fuerzas que actúan sobre la partícula, y
b)
la velocidad angular en función del tiempo.
♣ ♣ ♣