regla de cramer y teorema de rouché

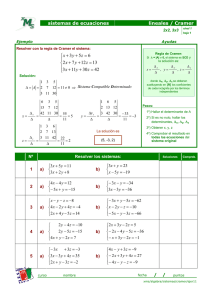
Regla de Cramer. Teorema de Rouché – Fröebenius.
4. SISTEMAS DE ECUACIONES
LINEALES.
REGLA DE CRAMER Y TEOREMA DE
ROUCHÉ -FRÖEBENIUS
Volvemos al tema de los sistemas de ecuaciones lineales, que ya vimos en el capítulo 1. Es pues
conveniente recordar los conceptos que se vieron entonces, como, la clasificación de los sistemas,
sistemas homogéneos, sistemas equivalentes.....
4.1. - Sistemas de Cramer.
Sea el siguiente sistema de n ecuaciones con n incógnitas:
a 11 x 1 + a 12 x 2 + ........... + a 1n x n = b 1
a 21 x 1 + a 22 x 2 + ........... + a 2n x n = b 2
.........................................
a n1 x 1 + a n2 x 2 + ........... + a nn x n = b m
En dicho sistema llamaremos matriz de coeficientes (M) a la matriz que contiene a los coeficientes de la
incógnitas, y matriz ampliada (M|b) a la matriz que contiene a los coeficientes y a los términos
independientes. También llamaremos matriz de términos independientes a la matriz que contiene dichos
términos (B), y matriz de incógnitas a la matriz columna X que contiene las incógnitas del sistema
Es decir:
a 11 a 12 ..... a 1n
Matriz de coeficientes: M =
a 21 a 22 ..... a 2n
...... ...... ..... ......
a n1 a n2 ..... a nn
Matriz ampliada; M|b =
a 11 a 12 ..... a 1n
b1
a 21 a 22 ..... a 2n
b2
...... ...... ..... ......
....
a n1 a n2 ..... a nn
bn
b1
Matriz de términos independientes: B =
b2
....
bn
x1
Matriz de incógnitas: X =
x2
.....
xn
1
MATEMÁTICAS II
Además un sistema de n ecuaciones con n incógnitas se puede poner de forma matricial de la siguiente
manera:
a 11 a 12 ..... a 1n
a 21 a 22 ..... a 2n
...... ...... ..... ......
x1
⋅
a n1 a n2 ..... a nn
x2
.....
b1
=
xn
b2
....
bn
Es decir:
M⋅X = B
Un sistema diremos que es de Cramer, si el número de ecuaciones coincide con el número de incógnitas
y además el determinante de la matriz de los coeficientes es distinto de cero.
Regla de Cramer:
a 11 x 1 + a 12 x 2 + ........... + a 1n x n = b 1
a 21 x 1 + a 22 x 2 + ........... + a 2n x n = b 2
Si el sistema
.........................................
es de Cramer entonces es COMPATIBLE
a n1 x 1 + a n2 x 2 + ........... + a nn x n = b m
DETERMINADO y la solución del mismo es:
b1
a 12 ..... a 1n
b2
a 22 ..... a 2n
...... ...... ..... ......
bn
x1 =
a n2 ..... a nn
|M|
a 11 b 1
..... a 1n
a 21 b 2
..... a 2n
...... ...... ..... ......
a n1 b n
x2 =
..... a nn
|M|
................................................
a 11 a 12 ..... b 1
a 21 a 22 ..... b 2
...... ...... ..... ......
a n1 a n2 ..... b n
xn =
|M|
Sea el siguiente sistema de Cramer
a 11 x 1 + a 12 x 2 + ........... + a 1n x n = b 1
a 21 x 1 + a 22 x 2 + ........... + a 2n x n = b 2
.........................................
a n1 x 1 + a n2 x 2 + ........... + a nn x n = b m
escrito en forma matricial será:
2
Regla de Cramer. Teorema de Rouché – Fröebenius.
M⋅X = B
Como |M| ≠ 0 existe por tanto la matriz inversa de M, M −1 y podemos multiplicar la expresión anterior por
M −1 por la izquierda:
M⋅X = B
M −1
⋅ M ⋅ X = M −1 ⋅ B
X = M −1 ⋅ B
Si sustituimos estas matrices por su valor tendremos:
x1
A 11 A 21 .... A n1
b1
x2
A 12 A 22 .... A n2
b2
....
..... .... .....
....
A 1n A 2n .... A nn
bn
.....
=
1
|M|
xn
luego:
b A + b 2 A 21 + ........ + b n A n1
x 1 = 1 11
|M|
x 2 = b 1 A 12 + b 2 A 22 + ........ + b n A n2
|M|
................................................
x n = b 1 A 1n + b 2 A 2n + ........ + b n A nn
|M|
Si se observa los numeradores de estas expresiones son, respectivamente los siguientes determinantes:
b1
a 12 ..... a 1n
b2
a 22 ..... a 2n
...... ...... ..... ......
bn
a n2 ..... a nn
Ejercicio
,
a 11 b 1
..... a 1n
a 21 b 2
..... a 2n
a 11 a 12 ..... b 1
...... ...... ..... ......
a n1 b n
, ............y
a 21 a 22 ..... b 2
...... ...... ..... ......
a n1 a n2 ..... b n
..... a nn
Comprobar que el siguiente sistema es de Cramer y resolverlo utilizando la regla de
Cramer
x + 2y − 4z = 1
2x − y − 5z = −1
x − y − z = −2
4.2. - Teorema de Rouché - Fröebenius
Sea el sistema de m ecuaciones y n incógnitas:
a 11 x 1 + a 12 x 2 + ........... + a 1n x n = b 1
a 21 x 1 + a 22 x 2 + ........... + a 2n x n = b 2
.........................................
a m1 x 1 + a m2 x 2 + ........... + a mn x n = b m
El teorema de Rouché-Fröebenius afirma:
Teorema ”La condición necesaria y suficiente para que un sistema de m ecuaciones lineales con n
incógnitas sea compatible, es que el rango de la matriz de coeficientes sea igual al rango de la matriz
3
MATEMÁTICAS II
ampliada”.
Demostración
El teorema afirma que
El sistema es COMPATIBLE  rangoM = rangoM|b
Veamos en primer lugar que:
Si el sistema es COMPATIBLE  rangoM = rangoM|b
Si el sistema es compatible, entonces tiene solución, es decir, existen n valores para las incógnitas
s 1 , s 2 , ......., s n que verifican todas las ecuaciones del sistema:
a 11 s 1 + a 12 s 2 + ........... + a 1n s n = b 1
a 21 s 1 + a 22 s 2 + ........... + a 2n s n = b 2
.........................................
a m1 s 1 + a m2 s 2 + ........... + a mn s n = b m
Si sustituimos b 1 , b 2 , ....., b n en la matriz ampliada tenemos:
M|b =
a 11 a 12 ..... a 1n
a 11 s 1 + a 12 s 2 + ........... + a 1n s n
a 21 a 22 ..... a 2n
a 21 s 1 + a 22 s 2 + ........... + a 2n s n
...... ...... ..... ......
....
a n1 a n2 ..... a nn
a m1 s 1 + a m2 s 2 + ........... + a mn s n
La última columna es combinación lineal de las restantes, luego a efectos del cálculo del rango puede
suprimirse y se tiene entonces que:
rangoM = rangoM|b
Veamos ahora que:
Si rangoM = rangoM|b  El sistema es COMPATIBLE
Si rangoM = rangoM|b = r, entonces existe al menos un menor de orden r distinto de cero.
Sea |C r | ≠ 0 el determinante r × r distinto de cero.
Eliminamos las ecuaciones que no intervienen en este menor (por ser combinación lineal de las r
ecuaciones que intervienen, el sistema que obtenemos es equivalente al inicial).
Consideramos las r incógnitas que intervienen en C r como principales y las otras como parámetros
(pasándolas a la derecha de las ecuaciones junto con los términos independientes), obtenemos asi un
sistema equivalente al inicial, y de Cramer ya que C r sería la matriz de coeficientes, luego el sistema
sería COMPATIBLE.
Conclusión:
rangoM = rangoM|b = n o de incógnitas
rangoM = rangoM|b
SISTEMA COMPATIBLE
SISTEMA COMPATIBLE DETERMINADO
rangoM = rangoM|b ≠ n o de incógnitas
SISTEMA COMPATIBLE INDETERMINADO
rangoM ≠ rangoM|b
SISTEMA INCOMPATIBLE
4