Fundamentos de la programación lineal Se llama - Unefa-io

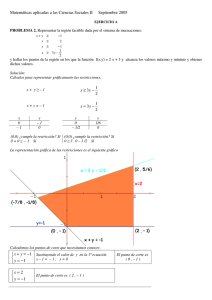
Fundamentos de la programación lineal
Se llama programación lineal al conjunto de técnicas matemáticas que pretenden
resolver la situación siguiente: Optimizar (maximizar o minimizar) una función
objetivo, función lineal de varias variables, sujeta a: una serie de restricciones,
expresadas por inecuaciones lineales.
Función Objetivo (F.O.): Para seleccionar qué función objetivo debe elegirse
se toma en cuenta lo siguiente:
a) Si vamos a encontrar situaciones en las cuales tendremos solo costos ya sea de
materia prima, costo de mano de obra, costo de uso de máquina, costos de transporte,
costos de depreciación ,etc. esto indica que indudablemente la F.O. será
de MINIMIZACION.
b) Si el enunciado solo da datos económicos de ganancia, precio de venta o dinero a
recibir por unidad producida la F.O. será de MAXIMIZACION.
c) Si el enunciado nos da al mismo tiempo costos y ganancias restaremos de la siguiente
manera: GANANCIAS – COSTOS = UTILIDAD, la que tendrá como F.O.
MAXIMIZACION.
d) Si no nos dan ningún dato económico y solo se da tiempos, el tiempo se minimiza, si
nos da solo producción, la producción se ha de maximizar, si el modelo corresponde a
contratar al personal, la función objetivo se minimiza.
Restricciones: Estas limitaciones o restricciones en los modelos lineales tienen
sólo las siguientes estructuras: <= , >=, =.
Muchos problemas tienen expresiones características que nos pueden anunciar
que tipo de restricción debemos usar, por ejemplo:
Usar
Para expresiones como :
<=
como máximo, a lo más, disponibilidad, demanda
máxima.
>=
como mínimo, por lo menos, al menos, demanda mínima.
=
total, proporción
Finalmente las restricciones deben tener las mismas unidades en tanto en su lado
izquierdo como derecho. La no negatividad de algunas variables son muy importante
para definir la solución de algunos modelos, por lo tanto se dice que todas las variables
son >=0.
Tipos de problemas de programación lineal
En un problema de Programación Lineal, según sean las restricciones, se
obtendrán poliedros diferentes, acotados o no, y según sea la posición de la función
objetivo respecto de dicho poliedro se pueden originar diferentes situaciones. Según el
tipo de soluciones que presenten un problema de Programación Lineal puede ser:
Factible: si existe la región factible. En este caso nos podemos encontrar:
Óptimo finito y único: La solución óptima está formada por un único punto con
coordenadas reales.
Múltiples óptimos: Un problema de Programación Lineal puede tener más de un
óptimo. Además, o bien el problema tiene un único óptimo, o bien, tiene infinitos
óptimos.
Óptimo infinito: Un problema de Programación Lineal puede tener un óptimo no
finito, es decir, la función objetivo puede tomar, un valor tan grande o tan pequeño
como se quiera sin abandonar la región factible.
Región factible no acotada, óptimo finito: La no acotación de la región factible no
implica necesariamente óptimo infinito. Puede ocurrir que la función objetivo alcance el
óptimo en la zona acotada de la región factible.
Región factible no acotada, óptimo finito e infinito: Puede darse el caso que todos los
puntos de una de las semirrectas que determinan la región factible no acotada sean
solución del problema.
No factible. Región factible vacía: El conjunto de restricciones de un problema de
Programación Lineal puede ser incompatible, conduciendo a una región factible vacía.
Programación Lineal
Formulación
En esta parte debemos considerar algo muy importante, hay una variedad de
aplicaciones de modelos lineales, en las siguientes paginas vamos a tratar de considerar
modelos lineales y sobre todo de mas aplicación al inicio del aprendizaje de
formulación de modelos lineales.
Problema 1.- (producción)
Una industria vinícola produce vino y vinagre. El doble de la producción de vino
es siempre menor o igual que la producción de vinagre más cuatro unidades. Por otra
parte, el triple de la producción de vinagre sumado con cuatro veces la producción de
vino se mantiene siempre menor o igual a 18 unidades. Halla el número de unidades de
cada producto que se deben producir para alcanzar un beneficio máximo, sabiendo que
cada unidad de vino deja un beneficio de S/8 y cada unidad de vinagre de S/2.
Solución:
Beneficio
Vino
Vinagre
S/8 / unidad
S/ 2 /unidad
Variable de decisión:
Xi= Número de unidades producidas de i(i=Vino, vinagre= 1,2) a elaborar.
Función Objetivo:
Max=8x1+2x2
Restricciones:
El doble de la producción de vino es siempre menor o igual que la producción de
vinagre más cuatro unidades:2x1<=x2+4 el triple de la producción de vinagre sumado
con cuatro veces la producción de vino se mantiene siempre menor o igual a 18
unidades.
3x2+4x1<=18
Modelo Lineal
Max = 8x1 + 2x2
Sujeto a:
2x1 - x2 <= 4
4x1 + 3x2 <= 18
No negatividad:
Xi>=0
Método gráfico
El método gráfico se utiliza para la solución de problemas de Programación
lineal, representando geométricamente a las restricciones, condiciones técnicas y el
objetivo.
El modelo se puede resolver en forma gráfica si sólo tiene dos variables. Para
modelos con tres o más variables, el método gráfico es impráctico o imposible.
Cuando los ejes son relacionados con las variables del problema, el método es
llamado método gráfico en actividad. Cuando se relacionan las restricciones
tecnológicas se denomina método gráfico en recursos.
Los pasos necesarios para realizar el método son nueve:
1. graficar las soluciones factibles, o el espacio de soluciones (factible), que
satisfagan todas las restricciones en forma simultánea.
2. Las restricciones de no negatividad Xi>= 0 confían todos los valores posibles.
3. El espacio encerrado por las restricciones restantes se determinan sustituyendo
en primer término <= por (=) para cada restricción, con lo cual se produce la
ecuación de una línea recta.
4. trazar cada línea recta en el plano y la región en cual se encuentra cada
restricción cuando se considera la desigualdad lo indica la dirección de la flecha
situada sobre la línea recta asociada.
5. Cada punto contenido o situado en la frontera del espacio de soluciones
satisfacen todas las restricciones y por consiguiente, representa un punto
factible.
6. Aunque hay un número infinito de puntos factibles en el espacio de soluciones,
la solución óptima puede determinarse al observar la dirección en la cual
aumenta la función objetivo.
7. Las líneas paralelas que representan la función objetivo se trazan mediante la
asignación de valores arbitrarios a fin de determinar la pendiente y la dirección
en la cual crece o decrece el valor de la función objetivo.
Ejemplo.
Maximizar
Z = 3X1 + 2X2
restricciones:
X1 + 2X2 <=6
(1)
2X1 + X2
<=8
(2)
-X1 + X2
<=1
(3)
X2 <= 2
(4)
>= 0
(5)
X2 >= 0
(6)
X1
Convirtiendo las restricciones a igualdad y representándolas gráficamente se tiene:
X1 + 2X2 = 6
(1)
2X1 + X2 = 8
(2)
-X1 + X2 = 1
(3)
X2 = 2
(4)
=0
(5)
X2 = 0
(6)
X1
Figura 1: Espacio de solución presentada con WinQsb
Figura 2: Determinación de solución
Maximizar
Z = 3X1 + 2X2
Punto
(X1, X2)
Z
A
(0, 0)
0
B
(4, 0)
12
C
(3.3, 1.3)
D
(2, 3)
12
E
(1, 3)
9
F
(0, 2)
4
12.6 ( óptima )
Solución Método Gráfico
Para obtener la solución gráfica, después de haber obtenido el espacio de
solución y graficada la función objetivo el factor clave consiste en decidir la dirección
de mejora de la función objetivo.
Realizado por los creadores del sitio:
http://www.unefa-io.webnode.es
Correspondiente a la unidad 2.
Investigación de Operaciones