trabajo práctico nº 3 determinación de redondez, esfericidad y

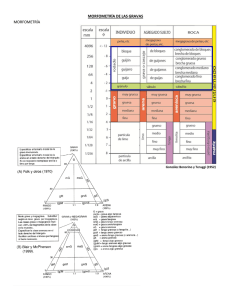
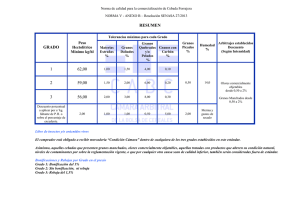
TRABAJO PRÁCTICO Nº 3
DETERMINACIÓN DE REDONDEZ, ESFERICIDAD Y ECUANTICIDAD
La morfología de los fragmentos (shape = forma), la redondez y la pivotabilidad (o rotabilidad)
constituyen propiedades de gran significación sedimentológica, en lo que respecta al efecto que tienen
sobre el transporte. Estas propiedades revelan además, las modificaciones sufridas por los granos
angulosos de distintas formas por efectos de la abrasión, selección por transporte y solución. Pese a su
gran importancia los trabajos referentes al tema son escasos, debido posiblemente a que los
procedimientos de obtención de los datos son largos y tediosos y a que constituyen uno de los aspectos
más difíciles de expresar numéricamente.
La morfología de los granos se define por medio de una serie de razones entre el eje mayor a, el
intermedio b y el menor c (perpendiculares
entre sí) aunque no se cortan en un mismo punto
(Fig. 3.1). Existen dos aspectos fundamentales
en la morfología de los clastos: la forma y la
esfericidad, mientras que la redondez y la
pivotabilidad, son independientes de la
morfología y expresan aspectos distintos.
Figura 3.1. Medición de rodados y la posición
de los ejes mayor (a), intermedio (b) y menor (c)
(Krumbein, 1941 en Pettijhon, 1957, 1970).
I- Forma
La forma de un clasto puede definirse de acuerdo a las características geométricas o la relación
entre los ejes de un rodado. Mediante la aplicación del concepto de forma se puede distinguir entre un
rodado prolado (un eje largo y dos cortos) de otro oblado (dos ejes largos y uno corto).
La forma se define por la relación entre los ejes: c/b y a–b/a–c, como lo propusieron Sneed y Folk
(1958) en su diagrama triangular; o por medio de cuatro clases, como las propuestas por Zingg (1935),
basadas en los valores c/b y b/a (Fig. 3.2).
Figura 3.2. Clases de forma de granos según Zingg
(1935) y su relación con la esfericidad de Krumbein
(1941) (en Corrales Zarauza et al, 1977)
Clases de formas según Zingg:
Discoidales u Oblados: b/a > 2/3, c/b < 2/3.
Esféricos o Equidimensionales: b/a > 2/3, c/b > 2/3.
Elipsoidales o Triaxiales: b/a < 2/3, c/b < 2/3.
Cilíndricos o Prolados: b/a < 2/3, c/b > 2/3.
Planares: b/a de 0,05 a 1, c/b de 0 a 0,05.
Aciculares: b/a de 0 a 0,05, c/b de 0,05 a 1.
II- Redondez y Esfericidad
Consideraciones generales: La morfología de los fragmentos desprendidos de una roca es tan variada y
caprichosa, que resulta muy difícil establecer características comunes que permitan expresar sus
particularidades en números. De hecho se puede generalizar que los fragmentos recién desprendidos
presentan contornos muy angulosos, y tienden durante el transporte a redondear sus aristas. Este proceso
de redondeamiento, denominado atrición, actúa más eficientemente cuando la roca es de dureza y
coherencia homogénea. Un cristal con fácil clivaje difícilmente se redondea en las aristas de clivaje, pues
la atrición crea nuevas aristas agudas, a medida que el tamaño se reduce.
La mayor parte de los sedimentólogos ha convenido que existen dos magnitudes que pueden
expresar parte de las propiedades de los rodados:
a) la redondez: una expresión del grado de agudeza de las aristas y ángulos.
b) la esfericidad: expresa el grado de aproximación de la partícula a una esfera de igual volumen.
En este aspecto, un cubo es más esférico que un cuerpo tabular por más redondeado que sea este
24
último. Este detalle, da la pauta que ambos conceptos son independientes. Mientras que la redondez está
relacionada con la atrición que ha afectado a la partícula durante el transporte, sin influir en su movilidad,
la esfericidad incide sobre el comportamiento hidrodinámico. En condiciones de transporte por
suspensión las partículas de mayor esfericidad tienden a separarse de las otras menos esféricas y a
sedimentarse por decantación (en partículas de igual volumen la forma esférica siempre tiene menor
superficie y por ende menor fricción con el medio). Por el contrario, cuando el transporte es por tracción
la forma menos esférica tiende a quedar rezagada con respecto a las partículas esféricas (Pettijohn, 1970).
Los factores que más influyen en la esfericidad y redondez de un clasto, son los siguientes:
1) la forma original del clasto (litología)
2) la estructura del fragmento (esquistosidad, fisilidad, clivaje, diaclasas)
3) resistencia a la atrición (resistatos)
4) naturaleza del agente de transporte
5) energía del agente de transporte y condiciones de transferencia de ésta, entre el medio y el
clasto
6) duración e intensidad de las condiciones precedentes.
La esfericidad y la redondez constituyen parámetros texturales de importancia relevante en los
sedimentos clásticos. La esfericidad refleja principalmente las condiciones de depositación en el momento
de acumulación y depende muy poco de los procesos de abrasión ocurridos (Pettijohn, 1975). El efecto
del transporte sobre la esfericidad y redondez de los clastos parecería también indicar la diferencia entre
estas propiedades, mientras que la redondez aumenta rápidamente al principio del transporte (ajustándose
a una curva exponencial) y luego aumenta lentamente con la distancia de transporte. Por otro lado, el
aumento de la esfericidad es más lento y muestra pocos cambios con la distancia de transporte (Fig. 3.4).
Figura 3.4. Relaciones entre
esfericidad, redondez y la distancia
de transporte (Griffiths, 1967 en
Corrales Zarauza et al 1977).
Según Griffiths (1967) los
estudios de la forma de los granos
reflejan el grado y la intensidad de los
procesos de selección y pueden ser
usados para diferenciar ambientes,
aunque no para dilucidar problemas
de proveniencia. Cuando se comprueba la presencia de esfericidades muy bajas, éstas reflejan la acción
química que acompaña a episodios diagenéticos especiales (Griffiths, 1967).
La meteorización de las rocas produce granos que poseen un grado variable de esfericidad y
redondez. Si suponemos que todos los valores de esfericidad y redondez son posibles, los estudios sobre
esfericidad y redondez difícilmente pueden distinguir entre distintas fuentes. Los resultados pueden, por
el contrario, proveer de información acerca de los procesos de erosión, transporte y sedimentación. Sin
embargo, la redondez puede estar afectada por la contribución de fuentes distintas como lo determinó
Banerjee (1964) que encontró una relación inversa tamaño-redondez (los granos más grandes eran menos
redondeados) en contra de lo que normalmente se espera: los granos mayores se redondean más rápido en
las mismas condiciones de transporte.
a) Esfericidad
Es una medida convencional que expresa el grado en que una partícula se aproxima a una esfera.
Wentworth (1922) fue el primero en desarrollar una expresión que indica la forma de las partículas. Se
trata de su Coeficiente de aplastamiento, expresado por ra/R, donde ra es el radio de curvatura de la cara
más plana y R el radio medio. El mismo autor también desarrolló la expresión de redondez r i/R, donde ri
es el radio de curvatura de la arista más aguda.
Wadell (1932) propuso la medida de esfericidad verdadera que es igual a s/S donde “S” es el área
de la superficie de la partícula y “s” el área de la superficie de una esfera del mismo volumen. En
consecuencia, la esfericidad expresada así, es el área de la partícula por unidad de volumen.
Sneed y Folk (1958) revisaron las distintas mediciones de esfericidad y propusieron una nueva: la
esfericidad máxima de proyección, Φp (también denominada esfericidad efectiva de sedimentación), que
25
es igual a la razón entre una sección principal de una esfera de igual volumen y el área máxima de
proyección del rodado, se expresa cuantitativamente como:
Φp = 3√ (C2/AB)
en términos de los cocientes B/A y C/B:
Φp = 3√ B/A · (C/B)2
según estos autores, la ecuación representa mejor el comportamiento de una partícula en un medio
fluido, que las indicadas previamente. Se puede calcular la esfericidad máxima de proyección
gráficamente. Sin embargo, Briggs et al. (1962) han demostrado que también las otras mediciones se
correlacionan bastante bien con las propiedades dinámicas de las partículas.
La medición de la esfericidad y de la redondez puede realizarse directamente sobre la partícula o
por comparación con una carta con formas patrones (ej.,
Rittenhouse, 1943). La dificultad de medición de la
esfericidad de Wadell (1933, 1935) movió a ese autor a
utilizar la esfericidad definida por Tickell (1947) igual a
dc / Dc, donde dc es el diámetro del círculo de igual área
(medido con un planímetro) y Dc es el diámetro menor
circunscripto. Sin embargo, Tickell (1947) se inclina por
la fórmula de Riley (1941) Ri = (di / Dc)1/2, donde di y Dc
son el círculo máximo inscripto y mínimo circunscripto,
respectivamente, fórmula que utilizaremos en el trabajo
práctico (Fig. 3.5). Todos estos procedimientos, son
aplicables a granos de cuarzo, pues en el caso de las
micas (aplanadas fuertemente según c) se comete un error
muy grande al usar la proyección de la vista según ab.
Figura 3.5. Esfericidad de Riley (1941).
b) Redondez
La redondez de los clastos de grava y arena deberían ser notadas en cualquier descripción de roca,
aunque no es generalmente mencionada en el nombre corto para los sedimentos detríticos. La redondez
indica el grado de abrasión a que han sido sometidos los granos; refleja la historia de transporte. La
redondez no necesariamente refleja la distancia que han viajado los granos de su área fuente: los granos
redondeados pueden haber derivado locamente de rocas sedimentarias o pueden haber sido intensamente
erosionadas en un ambiente cercano a la fuente, tal como una playa adyacente a un acantilado. Debido a
que las olas proveen condiciones de alta energía, la zona de olas activas de playa es el ambiente subácueo
más efectivo para el redondeamiento físico de los granos sedimentarios. El retrabajado eólico en playas o
dunas de interior es aún más efectivo en tal proceso debido a que el agua tiende a “amortiguar” algunos
de los procesos de abrasión (ej. impacto). En algunos suelos, la acción química redondea los granos
(Crook, 1968).
Cuantitativamente, la redondez verdadera expresada por la fórmula de Wadell (1933) es:
d=Σ(ri/R)/N
donde d es la redondez, ri es el radio de
curvatura de la esquina i, R es el radio del
círculo máximo inscripto y N es el número de
esquinas consideradas. Este procedimiento, sin
embargo, está sujeto a ambigüedades, pues no se
tiene en cuenta las superficies con radio de
curvatura superior a R, lo que determina que dos
partículas como las de la figura 3.6 posean igual
redondez aunque visiblemente no la tienen.
Figura 3.6. Naturaleza geométrica de la
redondez en las gravas (Krumbein, 1940 en Pettijohn, 1975).
26
Una aproximación mayor se obtiene determinando la redondez en tres vistas de la partícula (a-b, bc y c-a) y promediando los valores obtenidos, aunque la definición de Wadell (1932) establece claramente
que la redondez se mide en dos direcciones, que por razones obvias inherentes a la fórmula a aplicar, debe
ser el plano ab.
Powers (1953) y Krumbein (1941), prepararon escalas de redondez gráfica, aplicables a los granos
de arena, que permiten obtener valores bastante precisos.
La redondez en los granos dentro de un sedimento variará comúnmente aún si todos los granos han
estado sujetos a la misma historia de abrasión (o solución). Varios minerales y fragmentos de rocas
difieren en sus propiedades físicas y químicas, ejemplo: dureza, brillo, tipo de anisotropía y solubilidad.
Sin embargo, en la comparación de las muestras es necesario contrastar la redondez en un mismo tipo de
componentes. El cuarzo es el más usado comúnmente en areniscas debido a que es abundante, duro y
tiene propiedades físicas y químicas relativamente isótropas. Además, los granos de diferente tamaño se
redondean a velocidades diferentes como resultado de que los procesos de abrasión son más efectivos en
los granos más grandes. De ahí que para descubrir un patrón entre las muestras, se deberían analizar los
mismos tamaños de grano. Cabe agregar que en cualquier conjunto de granos el grado de redondeamiento
se espera que disminuya con el decrecimiento del tamaño de grano. Si los granos de cuarzo más gruesos
en una muestra son menos redondeados que los más pequeños, está claro que la mayor parte de la
fracción gruesa tiene una historia diferente a la fracción fina, independientemente de la distribución de
tamaños del conjunto.
No-Normalidad de las densidades Esfericidad y Redondez
Curray y Griffiths (1955) determinaron la esfericidad y redondez en granos de cuarzo de tres tipos
de rocas: arcosas, grauvacas y cuarcitas (clasificadas según Krynine, 1948) en diferentes formaciones.
Las diferencias de esfericidad no son significativas estadísticamente entre distintos tipos de rocas, aunque
las arcosas son las menos esféricas, las grauvacas intermedias y las cuarcitas las más esféricas. La
redondez determinada por comparación visual en el tamaño de grano 125 micrones, muestra también a las
arcosas como las menos redondeadas y las cuarcitas como las más. Sin embargo, la distribución de
frecuencia de la redondez es marcadamente normal, abundan mucho más los términos más redondeados y
la curva es excesivamente leptocúrtica (los valores más abundantes están concentrados junto a la media).
III- Pivotabilidad o Rotabilidad
El concepto de índice de pivotabilidad fue introducido por Shepard y Young (1961) y elaborado
posteriormente por Kuenen (1964) y se define como el ángulo mínimo de pendiente que determinará que
una partícula rote o caiga. Winkelmolen (1969) ha realizado un exhaustivo estudio de este aspecto de la
morfología de las partículas e introdujo el término rotabilidad. La rotabilidad es una propiedad de las
partículas derivada de su forma y
redondez, tal como se ve en la figura 3.7.
Es en esencia una descripción de forma
funcional, en contraste con los otros
conceptos que son puramente numéricos.
El valor correspondiente se mide en un
aparato ideado por ese autor, donde se
sueltan algunos granos de la arena que se
quiere estudiar. El estudio con este
procedimiento de varias arenas de duna y
playa
ha
permitido
distinguir
perfectamente entre ellas, ploteando la
rotabilidad vs. tamaño de grano.
Figura 3.7. Pivotabilidad o rotabilidad
(según Kuenen 1964, adaptado de
Corrales Zarauza et al., 1977).
Significado geológico de los datos morfométricos
En la mayoría de los casos de estudio se determina la morfometría de los clastos a partir del
relevamiento de entre 25 a 100 individuos por localidad de muestreo, de donde se extraen promedios que
luego se extrapolan a las poblaciones que las muestras representan. Aunque raramente realizado, se puede
también calcular la varianza y desviación típica de tales distribuciones de redondez.
La mayor parte de los estudios tridimensionales han sido llevados a cabo en gravas, mientras que
27
para arena se suele apelar a secciones delgadas donde se mide la morfología por la relación entre el largo
máximo visible y el más corto o se estudia la textura superficial de los granos mediante microscopio
electrónico de barrido (SEM en inglés).
Se considera la morfología de los fragmentos como de poca importancia ambiental, aunque la
experiencia acumulada en cuanto a comportamiento aero e hidrodinámico indica que ésta afecta
considerablemente su comportamiento. Debido a eso se han intentado tantos factores de morfología, que
tratan de poner en evidencia el efecto de éstos en el comportamiento hidrodinámico (en la velocidad de
caída por ejemplo, en Schultz et al. 1954). Sin embargo, la dependencia de la morfología con la forma
original y las propiedades internas de cada fragmento, hacen muy poco visible la relación entre
morfología y ambiente depositacional. Briggs et al. (1962) han demostrado que la morfología es tan
importante como la densidad en la distribución de los minerales pesados.
El grado de redondez de una partícula depende del tamaño, características físicas e historia
abrasiva. Los estudios de laboratorio y medición de la redondez en arenas de sedimentos modernos
demuestran que el redondeamiento es un proceso muy lento, y se hace más lento cuando menor es el
tamaño de grano (o sea que dada una distancia de transporte, los granos mayores se redondean más
rápidamente). Los experimentos de Kuenen (1959) demostraron que 20.000 km de transporte sólo
producen una disminución de peso no superior al 1%, en granos medianos y angulosos de cuarzo. Aunque
uno desearía estimar la distancia de transporte, determinando el porcentaje de granos angulosos o la
redondez promedio, tal cosa es imposible pues las causas que gobiernan el proceso de redondeamiento
son poco conocidas. Uno de los inconvenientes es que el ritmo de redondeamiento varía con el ambiente
depositacional o el ritmo depositacional. También la disolución química juega un papel importante en los
granos no silicatados.
Los granos bien redondeados son el resultado de varios ciclos sedimentarios, cada uno de los
cuales contribuye con una porción de redondeamiento. Otra posibilidad sería que el ambiente
sedimentario sea propicio para un redondeamiento muy rápido. Tal sería el caso de depósitos de playa o
duna, que se supone, produjeron granos bien redondeados en épocas geológicas pasadas debido a la
persistencia especial de esos ambientes; tal situación no ha sido confirmada en ambientes actuales
similares donde la arena no es más redondeada que la que ingresa recién al ambiente.
Debido a la lentitud con que operan los procesos de redondeamiento, es imposible determinar
tendencias de redondeamientos en un área dada. Algunos autores han utilizado el concepto de
redondeamiento para definir asociaciones mínimas o sistemas de dispersión basados en la presencia o
ausencia de un determinado porcentaje de granos angulosos, en una de las fracciones granulométricas.
Las provincias de redondeamiento pueden usarse para definir la angularidad de los minerales pesados,
generalmente zircón y turmalina, como también de cuarzo. Los sobrecrecimientos redondeados en granos
de arena son una evidencia concreta de granos policíclicos pero su proporción es tan pequeña que no
pueden usarse regionalmente.
La luminiscencia introducida por Sippel (1968) permitió ampliar el panorama para muchos
granos aparentemente homogéneos que no mostraban crecimiento secundario y que podrían pertenecer a
más de una generación (o ciclo diagenético).
28
DESARROLLO DEL TRABAJO PRÁCTICO Nº 3



Objetivos
Medición de las características de los rodados: tamaño y forma.
Comparación con las cartillas de redondez y esfericidad.
Cálculo de la redondez y esfericidad mediante gráficas y ecuaciones.
Materiales
Cátedra
Muestras de gravas
PC con programa estadístico de cálculos
Impresora
Alumnos
Regla, escuadra o escalímetro
Compás
Cartillas de redondez y esfericidad
Diagrama de Zingg
Papel cuadriculado o milimetrado
Calculadora
I- Medición de Rodados
a) Realice la medición de los tres ejes (A,B,C) (Fig. 3.1) en 5 rodados diferentes. Determine
redondez por comparación con las gráficas de Powers (1953) y la de Krumbein (1941) (ver TP
2, Fig. 2.3).
b) Elija tres rodados diferentes, proyecte los mismos en un papel y determine en cada caso:
1) Esfericidad según el método de Riley (1941) (Fig. 3.4).
2) Redondez según el método de Wadell (1933) (Fig. 3.5).
3) Compare la esfericidad obtenida en b)1) y la que se puede determinar en el diagrama donde
muestra la relación entre esfericidad y los índices de Zingg (Krumbein, 1941) (Fig. 3.7).
c) Calcule la ecuanticidad y grafique los resultados en el diagrama de esfericidad verdadera de
Spalletti (1985) (Fig. 3.8).
ECUANTICIDAD (√C/A)
1
ME 0,9
ESFERICA
0,8
E
SE
I
M
B
SUB - ESFERICA
0,7
0,6
0,5
NO ESFERICA
0,4
MB 0,3
0,2
0,1
SPALLETI 1984
0
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
MA
A SA SR
R
1
BR
REDONDEZ
Figura 3.7. Plantilla detallada para calcular la
esfericidad (Krumbein, 1941)
Figura 3.8. Diagrama de esfericidad verdadera de
Spalletti (1985).
II- Determinación de Parámetros Morfométricos
a) Con ayuda de un programa estadístico, determinar los valores de los parámetros morfométricos de un
conjunto de valores axiales pertenecientes a muestras del Río Vipos, extraídos en las tres estaciones.
b) Con los resultados obtenidos:
29
1) Determinar la frecuencia de cada clase textural en la estación de medición (Tabla 3.1). Realice un
histograma. ¿Cuál es la clase textural más frecuente?
2) Ídem anterior para cada litología.
3) Determine la frecuencia de cada forma (oblados, laminares, prolados y ecuantes) en cada clase
textural y en cada litología.
c) Con los datos obtenidos de tres estaciones diferentes, graficar:
1) Diámetro promedio vs distancia de transporte.
2) Platidad vs distancia de transporte.
3) Ecuanticidad vs distancia de transporte.
III- Informe
 Elabore un informe con las gráficas obtenidas y la interpretación que de ellas obtiene.
 En caso de que las gráficas se aparten de los valores normales explique los posibles factores
determinantes.
Tabla 3.1. Mediciones de frecuencia de cada clase textural
Clases
Diámetros
Número
Frecuencia
%
> 256 mm
256 - 128 mm
128 - 64 mm
64 - 32 mm
32 - 16 mm
16 - 8 mm
8 - 4 mm
BIBLIOGRAFÍA
Banerjee, I. 1964. Size roundness relation in the Barakar Sandstones of the South Karanpura Coalfiel,
India. Sedimentology Volume 3, Issue 1, pages 22–28, March 1964
Briggs, L.I., McCulloch, D.S. y Moser ,F. 1962. The hydraulic shape of sand particles. J. Sediment.
Petrol. 32: 645–656.
Corrales Zarauza, I., Rosell Sanuy, J., Sánchez de la Torre, L.M., Vera Torres, J.A. y Vilas Minando, L.
1977. Estratigrafía. Editorial Rueda. 718 pp.
Crook, K.A.W., 1968. Weathering and roundness of quartz sand grains. Sedimentology, 11, 171-182.
Curray, J.R. y Griffiths, J.C. 1955. Sphericity and roundness of quartz grains in sediments. Bulletin of the
Geological Society of America 66:1075–1096.
Griffiths, J.C. 1967. Scientific Method in Análisis of Sediment. McGraw Hill. New York. 508 pp.
Krumbein, W.C., 1940. Flood gravel of San Gabriel Canyon, Bulletin of Geological Society of America,
51: 636-676.
Krumbein, W.C. 1941. Measurement and geological significance of shape and roundness of sedimentary
particles, Journal of Sedimentary Petrology 11 (1941), pp. 64–72.
Krynine, P.D. 1948. The megascopic study and field classification of the sedimentary rocks.J. Geol. 56,
130–165.
Kuenen, Ph. H., 1959. Sand – its origin, transportation, abrasion and accumulation. Geol. Soc. South
Arica 62, Annexure, 33 pp.
Kuenen, P.H. 1964. Pivotability sudies of snad by a shape-sorten. Developments in sedimentology 1: 207215
Pettijohn, F. J. 1957. Sedimentary Rocks, 2 nd edition. Harper and Row Publishers, New York. 628 pp.
Pettijhon, F.J. 1970. Rocas Sedimentarias, EUDEBA. 731 pp.
Powers, M.C. 1953. A New roundness scale for sedimetay particles. Journal of Sedimentary Petrology 23:
117-119
Rittenhouse, G. 1943. A visual method of estimating two dimensional sphericity, Journal of Sedimentary
Petrology 13: 79–81.
30
Riley, N. A., 1941, Projection sphericity: Jour. Sedimentary Petrology, v. 11, p. 94-97.
Schulz, .F., Wilder, R.H. y Albertsonm, .L. (1954) Influence of shape on the fall velocity of sedimentary
particles. Colo. agric. Mech. Coll. ; Missouri River Div. Sedim. Ser. 5. 161 pp.
Shepard y Young, 1961 F.P. Distinguishing between beach and dune sands, Journal of Sedimentary
Petrology 31: 196–214.
Sippel, R.F. 1968. Sandstone petrology, evidence from luminescence petrography. J. Sediment. Petrol.
38: 530-554
Sneed E.D. y Folk, R.L. 1958. Pebbles in the lower Colorado River, Texas, a study in particle
morphogenesis, Journal of Geology 66(2): 114-150.
Spalletti, L.A., 1985. Revisión sobre el significado sedimentológico de algunas propiedades
morfométricas, con especial referencia a los conceptos de ecuanticidad y esfericidad verdadera de
los clastos. Boletín sedimentológico. Año 2 y 3: 67-77. Facultad de Ciencias Naturales. Instituto
de Geología. Cátedra de Sedimentología.
Tickell, F.G. 1947. The examination of fragmental rocks, 3ª edición. Stanford University Press. 154 pp.
Wadell, H. 1932. Volume, shape, and roundness of rock particles, Journal of Geology 40: 443–451.
Wadell, H. 1933. Sphericity and roundness of rock particles, Journal of Geology 41 (1933), pp. 310–331.
Wadell, H. 1935. Volume, shape and roundness of quartz particles, Journal of Geology 43: 250–280.
Wentworth, C.K. 1922. A scale of grade and class terms for clastic sediments. Journ Geol, 30, 377–392
Winkelmolean, M. 1969. Experimental rollability and natural shape sorting of sand. Thesis. University
of Groningen. 141 pp
Zingg, T. 1935. Beitrage zur Schotteranalyse. Schweiz. Mineral. Petrogr. Mitt. 15: 39-140
31