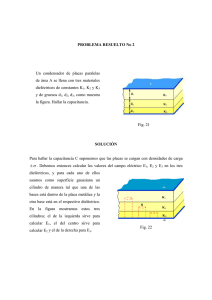
2 propiedades dieléctricas a baja frecuencia

Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades dieléctricas a baja frecuencia
2 PROPIEDADES DIELÉCTRICAS A BAJA FRECUENCIA
2.1 INTRODUCCIÓN
A bajas frecuencias la permitividad de un dieléctrico polar presenta una dependencia con la
frecuencia debida únicamente al mecanismo de la polarización orientacional, mientras que las
contribuciones debidas a los mecanismos de polarización iónica y electrónica presentan contribuciones
constantes. El comportamiento en frecuencia de este mecanismo orientacional es del tipo de relajación,
que en el caso del modelo de Debye viene caracterizado por un tiempo de relajación τ.
Los condensadores en capa fina se obtienen mediante la técnica de evaporación sucesiva en alto
vacío. Esencialmente están constituidos por una capa dieléctrica de espesor del orden de 1 μm, entre dos
capas metálicas que actúan de armaduras. La estructura del condensador se representa en la figura 1.
Figura 1
Además de las múltiples aplicaciones en el campo de los recubrimientos ópticos, los dieléctricos
en capa fina presentan también importantes aplicaciones en el campo de la microelectrónica, como son
los condensadores y los dispositivos MOS.
El objetivo de esta práctica es medir la dependencia de la parte real y la parte imaginaria de la
permitividad de un dieléctrico (SiOx) en el rango de bajas frecuencias (5-1x105 Hz). Se realiza la
representación de Cole-Cole para determinar los parámetros de ajuste al modelo de Davison-Cole.
2.2 FUNDAMENTO TEÓRICO
2.2.1
Permitividad relativa compleja
La capacidad de un condensador plano con dieléctrico el vacío o el aire viene expresada por la
conocida relación:
C0 = ε 0
S
d
(1)
La permitividad de un material caracteriza la respuesta del material al polarizarse bajo la acción
de un campo eléctrico. Esta respuesta depende de la frecuencia del campo aplicado y puede presentar un
retraso temporal por lo que en general será un valor complejo (εr'-jεr") y los valores de la parte real e
imaginaria dependerán de la frecuencia. Cuando entre las armaduras de C0 se coloca un medio dieléctrico
de permitividad compleja, el valor de la capacidad será: C = (εr'-jεr")C0. Si además el dieléctrico tiene una
cierta conductividad σ no nula, presentará una cierta resistencia R = d/σS (=ε0/σC0). El circuito
equivalente para representar este comportamiento, es la R en paralelo con C (ya que tanto R como C
experimentan la misma diferencia de potencial). La admitancia de este paralelo es:
2-1
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Y=
2.2.2
Propiedades dieléctricas a baja frecuencia
Cσ
1
+ jCω = 0 + ωε r ' ' C0 + jωε r ' C 0
R
ε0
(2)
Puente de impedancias
El puente de impedancias es un aparato de medida que en un determinado rango de frecuencias
(5Hz - 13MHz), aplica una tensión alterna de amplitud constante y de una frecuencia preseleccionada, y
mide las componentes de la corriente en fase y en cuadratura con la tensión de la señal aplicada. A partir
de estos valores calcula la admitancia compleja:
Y = Re(Y ) + j Im(Y )
(3)
En el modo de medida de capacidad (“C”), el puente de impedancias presenta el resultado de la
medida identificando la admitancia experimental (3) con el modelo dado en (2). En concreto a partir de la
componente en cuadratura, deduce el valor de la capacidad:
C = ε r ' C0 = Im(Y ) / ω
(4)
mientras que del cociente entre ambas componentes se deduce el valor de la tangente del ángulo de
pérdidas Q, o de su inversa D = Q-1:
D=
Re(Y ) ε r ' '+σ / ωε 0 r
=
Im(Y )
εr '
(5)
Una vez obtenidos los valores experimentales de C y D, estamos interesados en deducir los
valores de εr' y de εr". El valor de εr' se deduce directamente de la expresión (4) si se conocen los
parámetros geométricos S y d. Sin embargo la expresión (5) en general no proporciona directamente el
valor de εr", ya que aparece una contribución de σ, sino un valor "eficaz" εr"* que podemos expresar
formalmente como:
D=
2.2.3
ε r ' '*
εr '
donde ε r ' '* = ε r ' '+σ / ωε 0
(6)
Modelos teóricos de la permitividad dieléctrica
Las dependencias de εr'(ω) y εr"(ω) para la polarización dipolar vienen dadas en el modelo de
Debye para un sólo tiempo de relajación τ por las expresiones:
ε r ' (ω ) = ε r∞ +
ε r ' ' (ω ) =
ε r 0 − ε r∞
1 + ω 2τ 2
(7)
(ε r 0 − ε r∞ )ωτ
(8)
1 + ω 2τ 2
En la práctica, muy pocos dieléctricos siguen estrictamente el modelo de Debye, aunque presentan un
comportamiento cualitativamente similar. Davison y Cole sugirieron la siguiente fórmula empírica:
ε r * (ω ) = ε r∞ +
ε r 0 − ε r∞
(1 + jωτ )1−n
2-2
(9)
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades dieléctricas a baja frecuencia
con (0§n<1), que incluye el modelo de Debye como caso particular para n = 0. En la figura 2 se
representa como varía el diagrama de Cole-Cole para distintos valores del parámetro n. Se observa que
para n=0 (comportamiento tipo Debye), la gráfica Cole-Cole es una circunferencia si se utiliza la misma
escala para las unidades de εr'(ω) y εr"(ω).
Figura 2
En las Figuras 3 y 4 se representan como varían las dependencias de εr'(ω) y εr"(ω) para distintos
valores de n y τ respectivamente.
Figura 3
Figura 4
El valor máximo de εr" se encuentra para una frecuencia 1/τ que en los líquidos polares poco
viscosos (como por ejemplo el agua), se encuentra situada habitualmente en la región de las microondas
(τ≈10-9s, f≈109 Hz). Sin embargo en los materiales sólidos los valores del tiempo de relajación τ suelen
ser mucho más grandes. Los materiales obtenidos en capa fina presentan defectos cristalinos como
pueden ser vacantes o átomos intersticiales. Estos defectos originan la aparición de barreras de potencial
separadas por distancias grandes en comparación con las magnitudes moleculares. Esto da lugar a
fenómenos de relajación con valores de τ del orden de algunos segundos, y por tanto presentan un
máximo de εr" para una frecuencia del orden de algunas décimas de Hz.
2-3
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades dieléctricas a baja frecuencia
Si además el material presenta una conductividad σ, la εr"* presentará una contribución σ/ωεo que
se añade a εr" y que será dominante a bajas frecuencias. Este efecto se ilustra en las figuras 5 y 6 para el
agua, que tiene un comportamiento tipo Debye.
Figura 5
2.2.4
Figura 6
Circuito equivalente para un dieléctrico con relajación tipo Debye
El comportamiento de un dieléctrico con relajación tipo Debye se puede simular con el circuito
equivalente de la figura 7.
Figura 7
El condensador C2 sin resistencia serie representa los dipolos rápidos del material. El
condensador C1 en serie con R tiene un tiempo de relajación para su carga y descarga τ = R1C, y
representa los dipolos lentos.
Para bajas frecuencias (ω<<1/τ), el proceso de carga y descarga es suficientemente lento para que
los dos condensadores se carguen, y la capacidad equivalente tiende al valor C1+C2. Para altas
frecuencias (ω>>1/τ), el condensador C1 no es capaz de cargarse y descargarse al ritmo de la variación
del potencial aplicado, y es como si no estuviera, siendo la capacidad equivalente C2.
Nota: Aunque el circuito equivalente es útil para simular un comportamiento físico, hay que tener
presente que el origen físico del fenómeno es muy distinto en ambos casos. En un material con
comportamiento tipo Debye el origen es intrínseco al material que está formado por dipolos que necesitan
un tiempo relativamente grande para cambiar su orientación, y por tanto la correspondiente carga libre en
las armaduras del condensador. En el circuito equivalente el origen es extrínseco debido a la presencia de
la resistencia R en serie que retrasa la carga y descarga del condensador.
2-4
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades dieléctricas a baja frecuencia
2.3 REALIZACIÓN EXPERIMENTAL
2.3.1
Material
−
Analizador de impedancias (HP 4192A LF Impedance Analyzer) que puede medir en el rango de
frecuencias de 5 a 13 Mhz.
−
Caja conteniendo el circuito equivalente.
−
Caja conteniendo el condensador de SiOx.
−
Regulador de temperatura.
2.3.2
Procedimiento experimental
Las medidas se realizan en el modo de circuito paralelo.
−
Realizar la medida de Re(Y) y Im(Y) equivalentes para el circuito equivalente de forma manual
para las frecuencias de 100 Hz y 1 kHz. Deducir los valores de εreq' y εreq"* para el condensador
equivalente a la asociación, de espesor d y superficie S (ver valores numéricos en la caja).
−
Realizar la medida de Re(Y) y Im(Y) equivalentes para el circuito equivalente en el rango de
frecuencias de 100 Hz a 105 Hz. Ambos condensadores tienen una εr independiente de la
frecuencia, un mismo valor del espesor d y distintos valores de superficie S1 y S2. El proceso de
medida se controla mediante el programa “ANALYZER” a través de la interfase IEEE-488.
−
Realizar la medida a temperatura ambiente de Re(Y) y Im(Y) equivalentes para el condensador
de SiOx en el rango de frecuencias de 5 Hz a 105 Hz. El proceso de medida y de ajuste de
parámetros se realiza como en los apartados anteriores,
−
OPCIONAL: Repetir el proceso de medida para otras temperaturas (no superar 80 ºC. Consultar
con el profesor el manejo del controlador de temperatura).
2.3.3
Presentación de resultados
Para el circuito equivalente:
−
Deducir los valores de εr' y εr"*, para la frecuencia de 100 Hz haciendo el cálculo
correspondiente.
−
Mediante el software que se facilita (consultar al profesor), comparar las dependencias εreq'(ν) y
εreq"(ν) experimentales con el modelo teórico, y comprobar que verifican una dependencia tipo
Debye (n=0). Deducir los parámetros dieléctricos del ajuste con el modelo de Debye y comprobar
que verifican: εr0=(C1+C2)d/[ε0(S1+S2)], εr¶=C2d/[ε0(S1+S2)], τ=RC1 para una conductividad nula.
Para el condensador de SiOx:
−
Mediante el software suministrado, comparar las dependencias εr'(ν) y εr"(ν) experimentales con
el modelo teórico, y deducir los parámetros dieléctricos del material que sean accesibles. Se
procede del siguiente modo:
o
Representación de Cole-Cole (ver Figura 2): Esta representación es totalmente insensible
al valor del parámetro τ. La parte lineal de la representación permite calcular bien los
parámetros εr¶, y n.
o
Representación de epsilon en función de la frecuencia: en esta representación se pueden
deducir los otros parámetros: εro, σ y τ, donde σ da cuenta de la contribución de la
conductividad (σ/ωε0) a la parte imaginaria de la permitividad.
2-5
Laboratorio de Física de Materiales Dieléctricos y Ópticos
Propiedades dieléctricas a baja frecuencia
−
Representar el diagrama de Cole-Cole con los puntos experimentales (puntos sin línea) y la
dependencia calculada (línea sin puntos). Notar que en los dos ejes las escalas han de ser las
mismas.
−
Representar en gráficas distintas las dependencias de εr', εr'', y de tangδ= εr''/ εr' (con εr'' sin la
contribución debida a la conductividad), de manera análoga a la Figura 3, y la dependencia con la
frecuencia debida a la conductividad.
2.3.4
Elementos de discusión
−
Interpretar el significado físico de los valores observados de εr' para altas y bajas frecuencias.
−
Comparar el tiempo de relajación deducido con el del agua.
−
Discutir el ajuste del modelo con los datos experimentales. Intentar explicar las posibles
discrepancias.
2.4 BIBLIOGRAFIA
−
Apuntes de la asignatura.
−
J.M. Albella y J.M. Martínez, Física de los dieléctricos, Ed. Marcombo, Barcelona 1984.
−
L. Eckertová, Physics of thin films, Plenum Press, New York, 1986.
2-6