soluciónejercicio química modelo 0
Anuncio
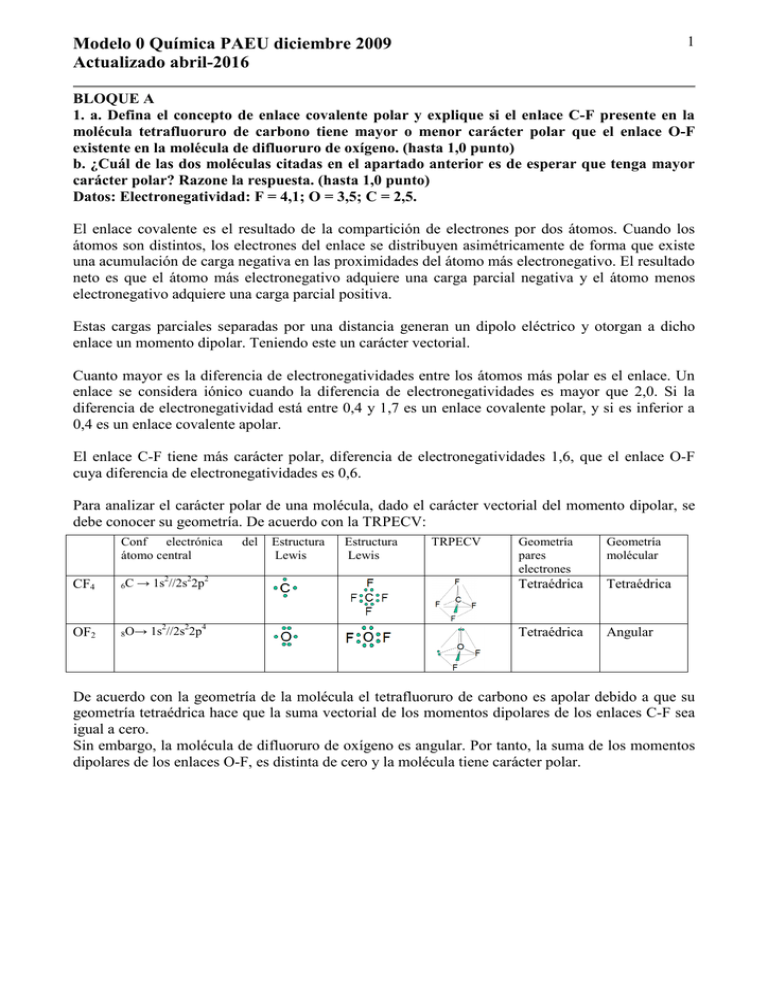
1 Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 BLOQUE A 1. a. Defina el concepto de enlace covalente polar y explique si el enlace C-F presente en la molécula tetrafluoruro de carbono tiene mayor o menor carácter polar que el enlace O-F existente en la molécula de difluoruro de oxígeno. (hasta 1,0 punto) b. ¿Cuál de las dos moléculas citadas en el apartado anterior es de esperar que tenga mayor carácter polar? Razone la respuesta. (hasta 1,0 punto) Datos: Electronegatividad: F = 4,1; O = 3,5; C = 2,5. El enlace covalente es el resultado de la compartición de electrones por dos átomos. Cuando los átomos son distintos, los electrones del enlace se distribuyen asimétricamente de forma que existe una acumulación de carga negativa en las proximidades del átomo más electronegativo. El resultado neto es que el átomo más electronegativo adquiere una carga parcial negativa y el átomo menos electronegativo adquiere una carga parcial positiva. Estas cargas parciales separadas por una distancia generan un dipolo eléctrico y otorgan a dicho enlace un momento dipolar. Teniendo este un carácter vectorial. Cuanto mayor es la diferencia de electronegatividades entre los átomos más polar es el enlace. Un enlace se considera iónico cuando la diferencia de electronegatividades es mayor que 2,0. Si la diferencia de electronegatividad está entre 0,4 y 1,7 es un enlace covalente polar, y si es inferior a 0,4 es un enlace covalente apolar. El enlace C-F tiene más carácter polar, diferencia de electronegatividades 1,6, que el enlace O-F cuya diferencia de electronegatividades es 0,6. Para analizar el carácter polar de una molécula, dado el carácter vectorial del momento dipolar, se debe conocer su geometría. De acuerdo con la TRPECV: Conf electrónica átomo central Geometría pares electrones Geometría molécular → 1s2//2s22p2 Tetraédrica Tetraédrica 1s2//2s22p4 Tetraédrica Angular CF4 6C OF2 8O→ del Estructura Lewis Estructura Lewis TRPECV De acuerdo con la geometría de la molécula el tetrafluoruro de carbono es apolar debido a que su geometría tetraédrica hace que la suma vectorial de los momentos dipolares de los enlaces C-F sea igual a cero. Sin embargo, la molécula de difluoruro de oxígeno es angular. Por tanto, la suma de los momentos dipolares de los enlaces O-F, es distinta de cero y la molécula tiene carácter polar. Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 2 BLOQUE A 2. Considerando los potenciales estándar de reducción correspondientes a los pares redox que se indican abajo: a. Justifique razonadamente cuáles son el oxidante y el reductor más fuertes presentes en dichos pares. (hasta 1,0 punto) b. Deduzca si es de esperar que, en las condiciones estándar, el yodo molecular oxide al hierro(II) hasta hierro(III) reduciéndose él a ión yoduro. (hasta 1,0 punto) Datos: E0(Fe3+/Fe2+) = +0,77 V; E0(Mn2+/Mn) = -1,18 V; E0(I2/I-) = 0,54 V. a. Las semirreacciones de reducción de los correspondientes pares son: reducción: Fe3+ + 1e- → Fe2+ E0 = + 0,77 V reducción: I2 + 2e- → 2IE0 = + 0,54 V reducción: Mn2+ + 2e- → Mn E0 = - 1,18 V Un buen reductor es el que cede electrones fácil (los metales son buenos reductores) Un buen oxidante es el que coge electrones fácil (los NO metales son buenos oxidantes) Las semirreacciones de reducción indican la “facilidad para coger electrones”, por tanto el hierro (III) será el mejor oxidante. Tiene el potencial de reducción más elevado y se reduce con facilidad a hierro(II) Fe3+ + 1e- → Fe2+ E0reducción = E0(Fe3+/Fe2+) = +0,77 V Si se escriben las semirreacciones de oxidación, ahora los E0 serán los de oxidación (cambio de signo): oxidación: Fe2+ → Fe3+ + 1e- E0 = - 0,77 V reducción: 2I- → I2 + 2eE0 = - 0,54 V 2+ reducción: Mn → Mn + 2e E0 = +1,18 V Las semirreacciones de oxidación indican la “facilidad para ceder electrones”, por tanto el Mn será el mejor reductor. Tiene el potencial de oxidación más elevado y se oxida fácilmente a Mn(II): oxidación: Mn → Mn2+ + 2e- E0oxidación = -E0(Mn2+/Mn) = +1,18 V b. Las semirreacciones que se deben dar en el proceso son: oxidación: Fe2+ → Fe3+ + 1e-E0(Fe3+/Fe2+) = -0,77 V reducción: I2 + 2e- → 2IE0(I2/I-) = 0,54 V global: 2Fe2+ + I2 → 2Fe3+ + 2I- E0reacción = -0,77 V + 0,54 V = -0,23 V < 0 Como el E0reacción es negativo, la reacción no es espontánea, el yodo molecular no es capaz de oxidar al hierro (II). 3 Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 BLOQUE A 3. Una disolución es 1,0·10-3 M en cloruro de bario y 1,0·10-2 M en cloruro de estroncio. Se añade cromato de potasio hasta que comienza a formarse un precipitado. a. Determine la naturaleza del precipitado. (hasta 1,0 punto) b. Calcule cuál es la concentración del ión cromato en ese momento. (hasta 0,5 puntos) c. ¿Que concentración del otro ión metálico se necesitaría para que ambos cromatos precipitaran en ese momento? (hasta 0,5 puntos) Datos: Kps (cromato de bario) = 1,6 · 10-10; Kps (cromato de estroncio) = 3,6 · 10-5. a. y b. La disociación del cloruro de bario es: BaCl2 → Ba2+ + 2 ClY la concentración de iones bario es: [Ba2+] = 1,0 · 10-3 mol/L La disociación del cloruro de estroncio es: SrCl2 → Sr2+ + 2 ClY la concentración de iones estroncio es: [Sr2+] = 1,0 · 10-2 mol/L Al añadir cromato de potasio se proporcionan iones cromato que hace que precipiten los cromatos insolubles (ver Kps de los datos) Ba2+ + CrO42- Sr2+ + CrO42- BaCrO4(s) SrCrO4(s) Cuando las respectivas sales comiencen a precipitar se tiene que cumplir que: Kps (BaCrO4) = [Ba2+] · [CrO42-] = 1,6·10-10 Kps (SrCrO4) = [Sr2+] · [CrO42-] = 3,6·10-5 Al añadir iones CrO42- comenzará a precipitar primero el compuesto que supere su Kps en primer lugar. Para que precipite el cromato de bario la concentración de iones cromato debe ser: [CrO 4 2 − ] = K ps ( BaCrO 4 ) [ Ba 2+ ] = 1,6 · 10 −10 1,0 · 10 −3 = 1,6 · 10 −7 mol / L Para que precipite el cromato de estroncio la concentración de iones cromato debe ser: [CrO 4 2 − ] = K ps ( SrCrO 4 ) [ Sr 2 + ] = 3,6 · 10 −5 1,0 · 10 − 2 = 3,6 · 10 −3 mol / L Por tanto el cromato de bario es la primera sustancia que comienza a precipitar y la concentración de iones cromato en ese instante es: [CrO42-] = 1,6·10-7 mol/L c. Para que precipite el cromato de estroncio es ese momento se tiene que cumplir que: [ Sr 2 + ] = K ps ( SrCrO 4 ) [CrO 42 − ] = 3,6 · 10 −5 1,6 · 10 −7 = 225 mol / L --------------------------------------Razonando de otra manera: Para que los dos cromatos comiencen a precipitar conjuntamente se tiene que cumplir que la relación entre las concentraciones de los cationes es: [ Sr 2 + ]· [CrO 4 2 − ] [ Ba 2+ ]· [CrO 4 2− ] = K ps ( SrCrO 4 ) K ps ( BaCrO 4 )] ; [ Sr 2 + ] [ Ba 2+ Despejando y como [Ba2+] = 1,0·10-3 mol/L ] = 3,6 · 10 −5 1,6 · 10 −10 = 2,25· 10 5 [Sr2+] = 1,0·10-3 mol/L · 2,25·105 = 225 mol/L 4 Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 BLOQUE A 4. Calcule la entalpía de la reacción de combustión del etanol: a. A partir de las entalpías de formación (en kJ/mol) siguientes: (hasta 1,0 punto) etanol(l) = -277,67; agua(l) = -285,84; dióxido de carbono(g) = -393,51. b. A partir de las entalpías de enlace (en kJ/mol) siguientes: (hasta 1,0 punto) C – C = 347; C – H = 414; C – O = 360; O=O = 498; C=O = 798: O-H = 464. a. La reacción de combustión del etanol es: CH3CH2OH(l) + 3O2(g) esteq ∆H0 (kJ/mol) 1 -277,67 3 2CO2(g) + 3H2O(l) 2 3 -393,51 -285,84 Como se proporcionan los datos de las entalpías de formación a esa temperatura de las distintas especies químicas, aplicando la ley de Hess y como el entalpía de formación del O2(g) es igual a cero al estar en su forma normal y teniendo en cuenta la estequiometría, se calcula la entalpía de reacción: ∆Hreacción = ΣHformación(productos) - ΣHformación(reactivos) = = 2 mol · (-393,51 kJ/mol) + 3 mol · (-285,84 kJ/mol) - 1 mol · (-277,67 kJ/mol) = -1366,87 kJ b. En la reacción hay que romper (∆H positivas, se absorbe energía): un enlace C-C 1·347 = 347 kJ cinco enlaces C-H 5·414 = 2.070 kJ un enlace sencillo C-O 1·360 = 360 kJ un enlace sencillo O-H 1·464 = 464 kJ tres dobles enlaces O=O 3·498 = 1.494 kJ TOTAL ENERGÍA ROMPER ENLACES = 4.735 kJ Nota: El agua está en estado líquido y las entalpías de enlace son para sustancias en estado gaseoso. No se tiene en cuenta aquí. Posteriormente se forman (∆H negativas, se desprende energía): cuatro dobles enlaces C=O 4·798 = 3.192 kJ seis enlaces O-H 6·464 = 2.784 kJ TOTAL ENERGÍA FORMAR ENLACES = 5.976 kJ ∆Hreacción = ΣHenlaces rotos - ΣHenlaces formados = 4.735 - 5.976 = - 1.241 kJ Los valores no coinciden por que las entalpías de enlace son valores promedio de esos enlaces en diversas moléculas. 5 Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 BLOQUE A 5. Nombre los siguientes compuestos: a) CH2=CH-CH3 ; CH2OH-CH2-CH2-CH2OH ; CH3 -O- C6H5 ; CH3 –CO-CH3 ; CH3-CH2-COOCH3. (hasta 1,0 puntos) b) Formule los siguientes compuestos: 2-metilheptano; 1,3-butadieno; fenol; ácido propanoico; etilamina. . (hasta 1,0 puntos) a. CH2=CH-CH3 CH2OH-CH2-CH2-CH2OH CH3 -O- C6H5 CH3 –CO-CH3 CH3-CH2-COOCH3 Propeno 1,4-butanodiol Etil-fenil-éter Propanona Propanoato de metilo. b. 2-metilheptano 1,3-butadieno fenol ácido propanoico etilamina Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 6 BLOQUE B 1. En relación con la estructura atómica: a. Escriba el nombre y la configuración electrónica completa y ordenada de los elementos de número atómico 15, 19, 23 y 34. (hasta 0,8 puntos) b. Enuncie el principio de exclusión de Pauli y la regla de Hund y deduzca razonadamente cuántos electrones desapareados tiene cada uno de los elementos, antes citados, en su estado fundamental. (hasta 1,2 puntos) fósforo (Z = 15): 1s2 2s2 2p6 3s2 3p3 potasio (Z = 19): 1s2 2s2 2p6 3s2 3p6 4s1 vanadio (Z = 23): 1s2 2s2 2p6 3s2 3p6 4s2 3d3 selenio (Z = 34): 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p4 El principio de exclusión de Pauli dice que dos electrones de un mismo átomo no pueden tener iguales sus cuatro números cuánticos. La regla de Hund o de máxima multiplicidad dice que los electrones, al ocupar orbitales de idéntica energía (degenerados), se distribuyen en el mayor número de orbitales posibles (máxima multiplicidad o desapareamiento). 7 Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 BLOQUE B 2. Calcule la energía reticular del cloruro de cesio utilizando un ciclo de Born-Haber elaborado con las magnitudes termodinámicas que se proporcionan. (hasta 2,0 puntos) Datos: ∆Hsublimación(cesio) = 78,2 kJ/mol; ∆Hdisociación(cloro) = 244 kJ/mol; ∆Hionización(cesio) = 375,7 kJ/mol; ∆Hafinidad electrónica(cloro) = - 348 kJ/mol; ∆Hformación(cloruro de cesio) = -442,8 kJ/mol. a) Energía de red, ∆H0red, de un sólido iónico AB es la energía asociada a la formación de un compuesto iónico a partir de un mol de cationes A+ y un mol de aniones B-, ambos en estado gaseoso, cuando se aproximan desde una distancia infinita hasta sus posiciones de equilibrio en la red cristalina. Es siempre una magnitud exotérmica y es la energía intercambiada en el proceso: A+ (g) + B- (g) →AB (s) En nuestro caso el proceso pedido es: Cs+ (g) + Cl- (g) → CsCl (s) ∆H0red Como ciclo termodinámico, la energía para llegar al CsCl (s) debe ser la misma por el camino 1 que por el camino 2. Por tamto: ∆H0formación, CsCl = ∆H0sublimación, Cs + ∆H0ionización, Cs + ½ ∆H0disociación, Cl2 + ∆Hafinidadelectrónica, Cl + ∆H0red Por tanto y sustituyendo: (todo en kJ/mol) - 442,8 = 78,2 + 375,7 + ½ 244 - 348 + ∆H0reticular ∆H0reticular = - 442,8 - 78,2 - 375,7 - ½ 244 + 348 = -670,7 kJ 8 Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 BLOQUE B 3. En un horno de combustión se quema una tonelada de pirita que contiene el 75 % en peso de disulfuro de hierro. Calcule: a. La masa de óxido de hierro (III) obtenido si el rendimiento del proceso de combustión es del 60 % (hasta 1,0 punto) b. El volumen de dióxido de azufre obtenido, en las condiciones anteriores, si el gas se recoge a 17ºC y a 850 mmHg de presión. (hasta 0,5 puntos) c. El volumen de oxígeno consumido en condiciones normales. (hasta 0,5 puntos) a. Se escribe la reacción y se ajusta: 4 FeS2 (s) + estequio. inicial final 4 6250 11 O2 (g) 2 Fe2O3 (s) + 8 SO2 (g) 11 z 2 8 x y Una tonelada de mineral son 106 g de mineral, de ellos el 75% es FeS2 (s), por tanto los moles iniciales de este compuesto son: nFeS 2 = 106 g pirita 75 g FeS 2 1 mol FeS 2 = 6250 mol FeS 2 100 g pirita 120 g FeS 2 Con la estequiometría de la reacción y el rendimiento de la misma, los moles de Fe2O3 (s) reales (x) que se obtendrán son: n Fe2O3 = 6250 mol FeS 2 2 mol Fe2O3 60 reales = 1875 mol Fe2O3 reales 4 mol FeS 2 100 teóri cos Y la masa de Fe2O3 (s) será: m Fe2O3 = 1875 mol Fe2O3 159,6 g Fe2O3 = 299250 g Fe2O3 reales 1mol Fe2O3 b. Análogo para el cálculo de SO2: n SO2 = 6250 mol FeS 2 8 mol SO2 60 mol reales = 7500 mol SO2 reales 4 mol FeS 2 100 mol teóri cos Aplicando la ecuación de los gases ideales y como 1 atm = 760 mmHg, resulta que: p · V = n · R · T; 850 mmHg 1 atm atm · L 5 · V = 7500 mol · 0,082 ( 273 + 17) K Y VSO2 = 1,59 · 10 L 760 mmHg mol · K c. Debido al rendimiento del proceso, la masa de oxígeno consumida es el 60 % de la cantidad estequiométrica. Como 1 mol de cualquier gas ocupa 22,4 L medidos en condiciones normales de presión y de temperatura: VO2 = 6250 mol FeS 2 11 mol O2 60 mol consumidos 22,4 L O2 = 2,31·105 L O2 consumidos en c.n. 4 mol FeS 2 100 mol teóri cos 1mol O2 Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 9 BLOQUE B 4. Para el equilibrio H2(g) + I2(g) X 2 HI(g), la constante de equilibrio es Kc = 54,8 a 425 ºC. a. ¿Cuáles serán las concentraciones en el equilibrio si 0,60 moles de HI se calientan a esta temperatura en un volumen de 1,0 litro? (hasta 1,2 puntos) b. ¿Cual es el porcentaje de disociación del HI? (hasta 0,8 puntos) Se construye la siguiente tabla, teniendo en cuenta que por cada α moléculas que se disocian de HI, se forman α/2 de H2 y α/2 de I2. I2 (g) H2 (g) + 2 HI (g) inicial (mol/L) 0 0 0,60 x x 0,60 -2x Aplicando la ley de Acción de Masas: K c = [ HI ]2 (0,60 − 2 x ) 2 ⇒ 54,8 = [ H 2 ]· [ I 2 ] x2 Calculando x: 54,8 = (0,60 − 2 x ) 2 0,60 − 2 x 0,60 ⇒ 54,8 = ⇒ 7,40· x = 0,60 − 2 x ⇒ x = = 0,064 mol / L 2 x 9 ,40 x Por tanto las concentraciones de las especies en equilibrio son: [HI] = 0,60 - 2·0,064 = 0,472 mol/L [I2] = [H2] = 0,064 mol/L * Comprobando si se cumple Kc: Kc = [ HI ]2 0,472 2 ⇒ = 54,4 ….. [ H 2 ]· [ I 2 ] 0,064 2 y Kc=54,8 resultado acorde con las aproximaciones en decimales de operaciones. El porcentaje de disociación del HI (α) será: α= 2x 2·0,064 n disociados = ⇒α = = 0,213 ⇒ α = 21,3% 0,60 0,6 n iniciales Modelo 0 Química PAEU diciembre 2009 Actualizado abril-2016 10 BLOQUE B 5. Necesitamos preparar 1 L de disolución de ácido nítrico 10-1 molar y en el laboratorio se dispone de ácido nítrico del 62,7 % en peso y densidad 1,38 g/cm3. a. Calcule el volumen que hay que utilizar de la disolución de ácido nítrico concentrada. (hasta 1,0 punto) b. Explique como procedería para preparar la disolución 10-1 M. (hasta 0,5 puntos) c. Nombre y dibuje el material de laboratorio que utilizaría. (hasta 0,5 puntos) a. Para calcular la molaridad de la disolución concentrada, se calculan los moles de HNO3 que contienen un litro de la misma. Esta será su molaridad: 1000 cm 3 disolución 1,38 g disolución 62,7 g HNO3 1 mol HNO3 = 13,73 mol / L 1cm 3 disolución 100 g disolución 63 g HNO3 Aplicando la ley de la conservación de la masa: los moles de ácido nítrico de la disolución diluida son los que deben ir en el volumen de la disolución concentrada que en la que se debe preparar. nconcentrada = ndiluida Mconcentrada · Vconcentrada = Mdiluida · Vdiluida Sustituyendo: 13,73·Vconcentrada = 0,1·1 Y Vconcentrada = 7,3·10-3 L = 7,3 cm3 de la disolución concentrada b. y c. Se vierte un poco de ácido comercial en un vaso de precipitados. Con una pipeta limpia y seca y ayudándonos con una pera de succión, se miden 7,3 cm3 de ácido comercial, que se vierten lentamente sobre un poco de agua destilada que contiene otro vaso de precipitados. La disolución se trasvasa a un matraz aforado y se rellena con agua destilada hasta un litro de disolución.






