no resistente

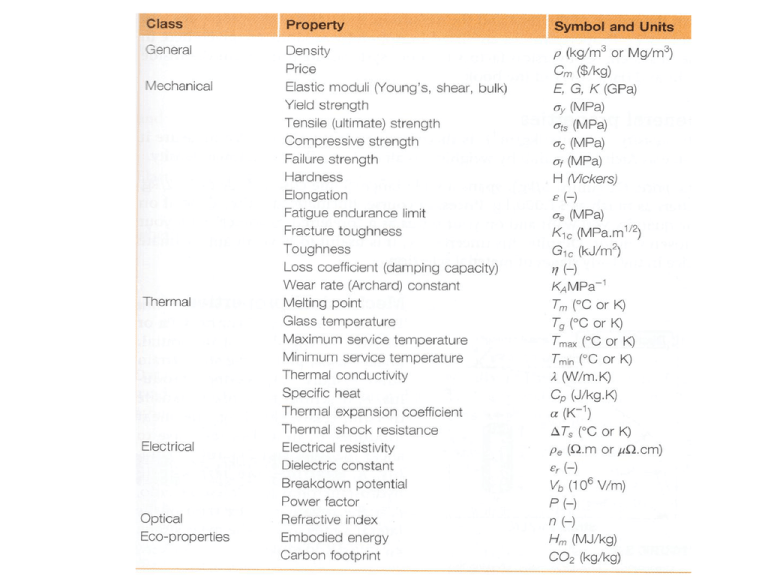
El ensayo de tracción
s= Ken
s = F/A0
esfuerzo
Hollomon
sT, resistencia a
la tracción
sf, resistencia a la
fluencia
módulo de
Young
E = (s2-s1)/(e2-e1)
sT, resistencia a
la ruptura
% elongación
(Lf-L0)/L0*100
s= Ee
% red. área
(A0-Af)/A0*100
Hook
módulo de
Poisson
(región elástica)
n = -Dr/DL
def. plástica
def. elástica
deformación
e = DL/L0
El ensayo de tracción
Resiliencia
esfuerzo
Tenacidad
def. plástica
def. elástica
deformación
propiedades - comportamientos
zona
Unidades (SI)
SI
Inglés
comportamientos
extremos
módulo de
elasticidad
GPa
kpsi
rígido-elástico
resiliencia
J/m3
Lb-in /in3
resiliente – no
resiliente
MPa
kpsi
resistente – no
resistente ¿debil?
propiedad
elástica
resistencia a la
fluencia
resistencia a la
tracción
plástica
resistencia a la
ruptura
% de elongación
Dúctil (maleable) frágil
%
% red. área
tenacidad
J/m3
Lb-in
/in3
tenaz – frágil
¿no tenaz?
Tenacidad a la fractura
Kc = √E Gc K = σ√∏a
Termino usado para describir la resistencia a la fractura cuando hay una
grieta de área a x t (a= radio o longitud de grieta , t =espesor del material)
Se llama también factor de intensidad de esfuerzo
En la cercanía de
la grieta, el
esfuerzo efectivo
es mayor, la
fisura intensifica
el esfuerzo.
Tenacidad a la fractura
Si se aplica una energía debido a una carga , para que la grieta avance
y ocurra una fisura se tiene que el trabajo debe ser mayor o igual a
El cambio de energia elástica + la energia absorbida por el esfuerzo
W ≥ δ U el + G tδa
La placa está sujeta ( no W)por lo que:
- δ U el = G tδa
( U el = energía elástica G = energía absorbida por unidad de área de
la grieta), tδa = área de grieta
Al crecer la grieta , se relaja elásticamente, se vuelve positivo
Uel,porque pierde energia elástica
Si se aplica una energía debido a una carga y consideramos un
elemento de volumen
Derivación de la Kc( tenacidad a
fractura crítica)
Tenacidad critica
el cubo tiene una energía de deformación
elástica :
½ σε o bien σ2/2E
Al introducir la grieta se relaja la energia elasticaen la línea punteada y
U el = σ2/2E. a 2 π t /2
Al propagar la grieta en δa ( derivamos)
(dU el/ δa )da = σ2/2E. 2 a π/ 2 t da y como - δ U el = Gc tδa
σ2 a∏ /2 E = Gc, se elimina el ½ y queda
σ 2 π a / E = Gc
o bien
σ √ π a = √ EGc
σ √ π a = K ( tenacidad a fractura) √ EGc = K c ( tenacidad crítica)
Determinación experimental
Problemas de Tenacidad a la Fractura
1.-Un piso de vidrio contiene microfisuras del orden de 2 micrones de longitud. El
vidrio tiene una tenacidad a la fractura de K ic = 0.6 MPa m ½ . Cuando se camina
sobre el piso las tensiones pueden ser tan altas como 30 MPa. ¿ Es seguro caminar
sobre ese piso?
2.- El fuselaje de un avión de pasajeros puede ser considerado como un tubo de
pared fina presurizado interiormente con un diámetro de 7 m y un grosor de 3 mm.
Está fabricado con planchas de Aluminio con tenacidad a la fractura de K ic de 100
MPa m 1/2 . A la altitud de crucero el indicador interno de presión marca 0.0.Mn/m2..
En una fila horizontal de remaches se han originado muchas grietas por fatiga y se
han unido para formar una grieta longitudinal que atraviesa el espesor del fuselaje.
Estimar la longitud crítica para que esta grieta se propague, produciendo la rotura
del fuselaje. ( La presión en un tubo se resuelve en una tensión en la pared de 𝞂 = p
r/t, en donde p= presión, r = radio, t = grosor)