F = mω2b [−cos(ωt) ı + 0 mωb2 [ − 1 Nulo

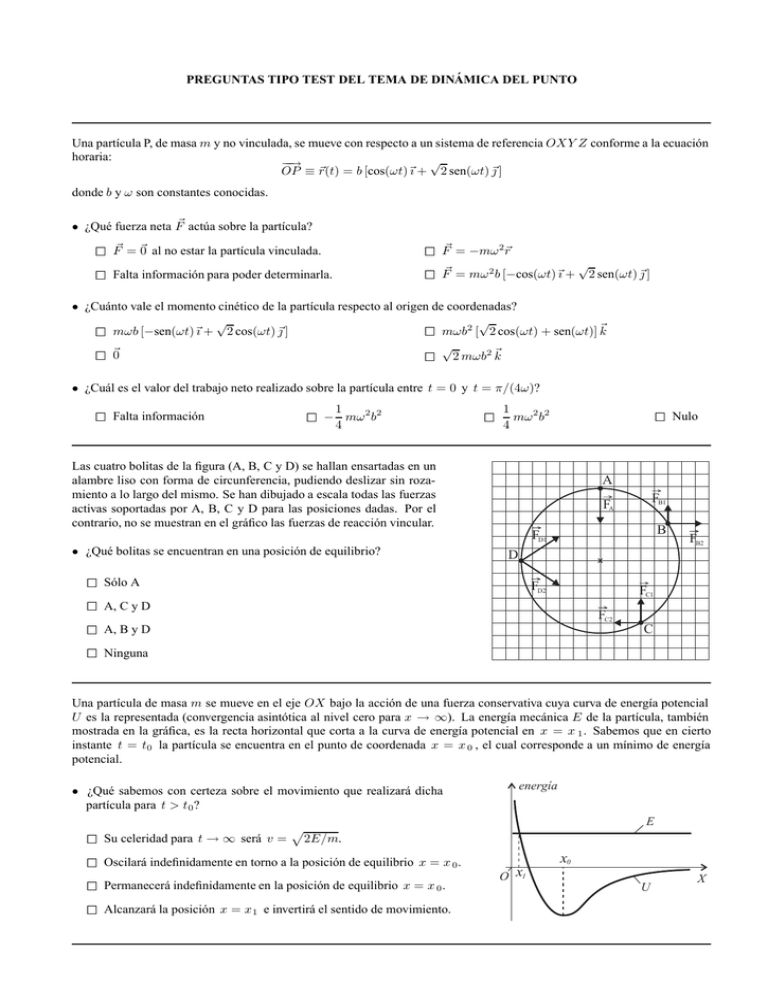
PREGUNTAS TIPO TEST DEL TEMA DE DINÁMICA DEL PUNTO
Una partı́cula P, de masa m y no vinculada, se mueve con respecto a un sistema de referencia OXY Z conforme a la ecuación
horaria:
√
−−
→
OP ≡ r(t) = b [cos(ωt)ı + 2 sen(ωt) j ]
donde b y ω son constantes conocidas.
• ¿Qué fuerza neta F actúa sobre la partı́cula?
2 F = −mω r
√
2 F = mω b [−cos(ωt)ı + 2 sen(ωt) j ]
2 F = 0 al no estar la partı́cula vinculada.
2 Falta información para poder determinarla.
2
2
• ¿Cuánto vale el momento cinético de la partı́cula respecto al origen de coordenadas?
√
√
mωb2 [ 2 cos(ωt) + sen(ωt)] k
mωb [−sen(ωt)ı + 2 cos(ωt) j ]
√
0
2 mωb2 k
2
2
2
2
• ¿Cuál es el valor del trabajo neto realizado sobre la partı́cula entre t = 0 y t = π/(4ω)?
2 − 41 mω b
2 Falta información
2
2 2
1
mω 2 b2
4
Las cuatro bolitas de la figura (A, B, C y D) se hallan ensartadas en un
alambre liso con forma de circunferencia, pudiendo deslizar sin rozamiento a lo largo del mismo. Se han dibujado a escala todas las fuerzas
activas soportadas por A, B, C y D para las posiciones dadas. Por el
contrario, no se muestran en el gráfico las fuerzas de reacción vincular.
2 Nulo
A
FB1
FA
B
FD1
• ¿Qué bolitas se encuentran en una posición de equilibrio?
FB2
D
2 Sólo A
2 A, C y D
2 A, B y D
2 Ninguna
FD2
FC1
FC2
C
Una partı́cula de masa m se mueve en el eje OX bajo la acción de una fuerza conservativa cuya curva de energı́a potencial
U es la representada (convergencia asintótica al nivel cero para x → ∞). La energı́a mecánica E de la partı́cula, también
mostrada en la gráfica, es la recta horizontal que corta a la curva de energı́a potencial en x = x 1 . Sabemos que en cierto
instante t = t0 la partı́cula se encuentra en el punto de coordenada x = x 0 , el cual corresponde a un mı́nimo de energı́a
potencial.
energía
• ¿Qué sabemos con certeza sobre el movimiento que realizará dicha
partı́cula para t > t 0 ?
E
Su celeridad para t → ∞ será v = 2E/m.
2
2 Oscilará indefinidamente en torno a la posición de equilibrio x = x .
2 Permanecerá indefinidamente en la posición de equilibrio x = x .
2 Alcanzará la posición x = x e invertirá el sentido de movimiento.
0
0
1
O x1
x0
U
X
Se tiene un sistema de cuatro partı́culas que interaccionan mediante fuerzas newtonianas. Se han representado gráficamente
a escala las fuerzas que la partı́cula 1 ejerce sobre las otras tres.
• ¿En cuál de estos gráficos la aceleración de la partı́cula 1 apunta en la dirección y sentido correctos?
4
F1
3
4
F1
3
4
F1
4
1
1
2
a
3
F1
F1
2
4
a
2
2
3
F1
3
4
F1
3
4
F1
2
a
2
2
4
3
a 1
1
F1
F1
3
F1
2
2
2
F1
2
2
Una partı́cula se mueve en el eje OX bajo la acción de una fuerza
conservativa. La función energı́a potencial U (x) y el nivel de energı́a
mecánica E de la partı́cula son los representados en la gráfica adjunta.
En el instante inicial la partı́cula se halla en la posición x = x 0 , la cual
se observa que corresponde a uno de los puntos de corte de E y U (x).
energía
U(x)
E
• ¿Por cuántas posiciones de equilibrio distintas pasará sin detenerse
la partı́cula en su movimiento?
2 Dos
2 Una
2 Ninguna
2 Tres
x0
O
X
Una partı́cula material, de masa m menor que 1 kg, experimenta una aceleración instantánea a debido a la acción simultánea
de dos fuerzas F1 y F2 . Se realiza una representación gráfica sobre un diagrama cuya cuadrı́cula corresponde a la unidad en
el SI de cada magnitud vectorial. Se tiene la certeza de haber representado bien las dos fuerzas, pero existen dudas sobre la
representación de la aceleración instantánea.
• ¿En qué único diagrama puede ser correcta la aceleración instantánea representada?
a
F1
a
m
F2
2
F1
m
F2
2
F1
a
m
F2
2
a
F1
m
F2
2
Una partı́cula de masa m desliza sin rozamiento a lo largo de una
rampa bajo el efecto de su propio peso. En el instante inicial, la
partı́cula se halla en reposo en el punto más alto de la rampa,
a una altura h. Al final de la rampa y apoyado sobre ella, hay
un resorte elástico OA de constante recuperadora k y longitud
natural l0 . Su extremo O está fijo (punto de anclaje), y su extremo libre A descansa sobre la rampa, a una altura h/6 cuando el
resorte está relajado.
2
h
A
O
• ¿Con qué celeridad v entrará en contacto la partı́cula con el extremo A del resorte?
5gh
5gh
2gh
v
=
v=
v=
3
6
2
m
g
2
h6
2 v=
5gh kl02
−
3
m
• ¿Cuánto vale la constante k del resorte si la partı́cula llega hasta el final de la rampa (punto O) con celeridad nula?
2 k = mgh
l
2
0
2 k = mgh
2l
2
0
2 k=0
2 k = 2mgh
l
2
0