Capítulo 2: Código detector de errores.

Capítulo 2:
Código detector de errores.
Materia: Teoría de la información y métodos de codificación.
Introducción
 Cuando un mensaje es transmitido es inevitable el ruido que degrada la
calidad de la comunicación. Cuando se detecta un error uno
simplemente repite el mensaje con la posibilidad de que la segunda vez
esté correcto o incluso en la tercera.
 Sólo es posible obtener errores si hay ciertas restricciones. El problema es
mantener esas restricciones en los posibles mensajes.
2.1 Repaso del módulo aritmético
Para dígitos binarios (1 y 0) las reglas de la adición están definidas por:
Por ejemplo:
Ocasionalmente trabajamos módulos diferentes a 2 para casos no binarios.
Teniendo un entero positivo ‘m’, para la adición y multiplicación mod ‘m’
dividimos el resultado en decimal por ‘m’ y tomamos el residuo no negativo.
Considerando que la información tenga 5 diferentes salidas 0,1,2,3,4. Procede
lo siguiente:
Casos especiales
 Otros casos del módulo 5 de adición y multiplicación pueden verse en las
siguientes tablas:
 Por la multiplicación mod ‘m’, tenemos que ser más cuidadosos si ‘m’ no
es primo. Suponiendo que tenemos los números ‘a’ y ‘b’ congruentes para
‘ a’ ’ y ‘ b’ ‘ modulo de modulos m. Esto significa:
 a ≡ a’ mod m and b ≡ b’ mod m ó
 a = a’+k1m and b = b’ +k2m
2.2 Errores independientes – ruido
blanco
 Para simplificar el análisis de prevención
de ruido, asumimos que los errores en un
mensaje cumplirán las siguientes
estipulaciones:
 1)La probabilidad de un error en cualquier
posición binaria es asumida de ser un
número p
 2) Errores en diferentes posiciones son
asumidas como independientes.
 El llamado “ruido blanco” es una analogía
con la luz blanca ya que contiene
uniformemente todas las frecuencias
detectadas por el ojo humano.
El “ruido blanco”
 Asumimos el ruido blanco en el
inicio porque es el caso más
simple, y es mejor empezar desde
el caso más imple y movernos a
situaciones más complejas
después de haber construido un
conocimiento concreto de un
caso simple.
Ejemplos del “ruido blanco”
 Considera un mensaje consistente de n dígitos por transmisión. Para el
ruido blanco, la probabilidad de no tener errores en cualquier posición
dada está dada por:
(1 − 𝑝)𝑛
 La probabilidad de que sólo haya un error en el mensaje está dado por:
𝑛𝑝(1 − 𝑝)𝑛−1
 La probabilidad de que l errores está dado por el (l + 1)mo término en la expansión
binomial.
Ejemplos, números pares
 Podemos obtener la probabilidad de un número par de errores (0,2,4…)
añadiendo las 2 siguientes expansiones binomiales y dividiendo entre 2:
 Denotando por |ξ | el más grande entero no es más largo que ξ.
Tenemos:
 Pr(un número par de errores)
2.3 Paridad simple – chequeo de
código
 La manera más sencilla de codificar un mensaje binario y hacer su error
detectable es contar el número de 1s en el mensaje, después agregar un
dígito binario elegido para que el mensaje cuente con un número par de
1s.
 Como hay (n-1) posiciones en el mensaje añadimos un chequeo de
posición de paridad ‘n’. Definido por xl el bit original en el lmo mensaje ∀1
≤ l ≤ n − 1, y dejar xn ser el bit de chequeo de paridad.
Paridad simple
 Por ejemplo, teniendo el mensaje (x1,x2,x3,x4) = (0111), el bit de paridad es
obtenido por:
 Xx5 = 0 + 1 + 1 + 1 = 1
 Y el código de paridad par de (x1,x2,x3,x4,x5) es (01111).
 Suponiendo que el mensaje es transmitido, pero un vector y = (00111) es
recibido. En este caso, un error en la segunda posición es encontrado.
Tenemos:
y1+y2+y3+y4+y5 = 0 + 0 + 1 + 1 + 1 = 1 (!=0);
 En este caso el error fue detectado. Sin embargo si otro vector de (00110) es
recibido, ósea 2 errores (en la segunda y última posición) han ocurrido.
 Ningún error se detectará ya que:
y1+y2+y3+y4+y5 = 0 + 0 + 1 + 1 + 0 = 0.
Paridad simple
 Evidentemente en este código cualquier número impar de errores pueden
ser detectados, pero cualquier número par de errores pasan
desapercibidos.
 Para los canales con ruido blanco (Pr) da la posibilidad de que cualquier
número par de errores en el mensaje. Dejando como primer término de Pr,
el cual corresponde a la probabilidad de no error, tenemos la siguiente
probabilidad de errores indetectables de un simple código de chequeo
de paridad aquí:
 Pr(errores indectetables)
Paridad simple
 La probabilidad de errores detectables, inclusive todos los errores impares
es obtenido por:
 Pr(errores detectables) =
 Para p muy pequeño tenemos:
 Pr(errores indetectables)=
Paridad simple
 Pr(Errores detectables)
 En la práctica, es común desarmar un mensaje largo en el alfabeto binario
en bloques de (n-1) dígitos y de añadir un dígito binario a cada bloque.
Esto produce la redundancia de:
 Donde la redundancia es definida como el número total de números
binarios dividido por el mínimo necesario.
2.4 El código ASCII
 Cada carácter en ASCII está representado de 7 datos de bits
constituyendo una secuencia binaria única. Esto nos da un total de 128
caracteres diferentes, los cuales son letras, números, controles especiales y
de puntuación.
2.5 Detector simple de errores rápidos
 En algunas situaciones los errores pueden ocurrir en ráfagas más que en
posiciones aisladas en el mensaje recibido. Por ejemplo, relámpagos,
fluctuaciones de suministros de poder, etc. Son causados principalmente
por sonido de ráfagas.
 Supón que el máximo tamaño de cualquier ráfaga de error que tenemos
que detectar es L. Para proteger los datos en contra de los errores de
ráfaga, primero debemos dividir el mensaje originar en una secuencia de
palabras consistiendo de L bits. Auxiliado con un código detector de
errores previamente elegido.
Errores de ráfaga
 Basado en el escenario anterior, si un error de ráfaga ocurre con una
palabra, en efecto sólo el error de una palabra es observado. Su un error
de ráfaga abarca el final de una palabra y el inicio de otra, aún así 2
errores correspondientes en las posiciones de las palabras se toparán y
asumiendo que cualquier tamaño de ráfaga cumple con 0 <= l <= L.
Considera lo siguiente como ejemplo:
 El mensaje es:
Hello NCTU
 Y el máximo L es 8, podemos usar ASCII y proteger el mensaje de errores
de ráfaga, el mensaje estaría así:
Hello NTCUn
Criterio de selección de caracter
2.6 Códigos de alfabeto más números
– códigos pesados
 El primer error humano es el intercambiar los números adyacentes; por
ejemplo, 38 se hace 83.
 El segundo error humano más común es 338 se hace 388, en adición la
confusión de O y 0 que también son muy comunes.
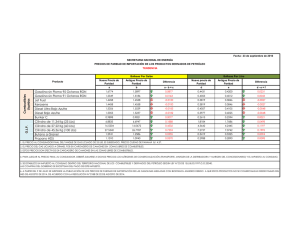
Un error se ha detectado porque el
check sum no es 00000000
Un error de tamaño 16 ha ocurrido pero
no se detectó
Alfabeto más números
 Es bastante común el uso de los alfabetos consistentes de 26 letras, un
espacio y los 10 dígitos decimales. Como el tamaño es de 37, siendo un
número primo, podemos usar el siguiente método para detectar la
presencia de los errores previamente mencionados.
 Obtenido un mensaje para codificar, ponemos pesos a los símbolos con
pesos 1,2,3,4… empezando con el dígito de chequeo del mensaje.
Después son sumados y reducidos al sobrante después de dividir por 37.
Ejemplo
 Asignamos un número distinto de {0,1,2,……,36} a cada símbolo en el
alfabeto/número de la siguiente manera: “0” = 0, “1” = 1 ….. “A” = 10, “B” =
11 y “espacio” = 36, después codificar: 3B8
 Procedemos con la digitalización progresiva y obtenemos una suma de
183. Como 183 mod 35 = 35 y 35 + 2 es divisible por 37, determinamos que
el número será “2” = 2
 Obteniendo: 3B82
2.7 Cooperación entre la redundancia
y la capacidad de detección de error
 Por una fuente de información de 8 diferentes salidas, obviamente cada
salida puede ser representada por un dígito binario de 3 elementos,
digamos (x1,x2,x3). Suponemos tres chequeos de paridad (x4,x5,x6) son
añadidos al mensaje original por las siguientes ecuaciones:
Redundancia y detección de errores
 Para formar una palabra codificada legítima (x1,x2,x3,x4,x5,x6).
Comparado con el chequeo de paridad simple, este código excede la
redundancia de 1/3 a 3/3. Dejamos (y1,y2,y3,y4,y5,y6) ser el vector
recibido como (x1,x2,x3,x4,x5,x6) es transmitido. Si al menos unos de los
checadores de paridad resulta erróneo el error es detectado.
Redundancia y detección de errores
 Por instancia, consideramos que el caso de un error en la i posición como:
 yi = xi +1 y yl = xl, ∀l ∈ {1,2,...,6} \ {i}.
 Sigue:
Redundancia y detección de errores
 Después de eso todos los errores pueden ser detectados. En adición,
considera el caso de un error doble, en i y en j respectivamente.
 Y tenemos: