Apunte Funciones Exc..

Algunas Funciones de Excel
Funciones Estadísticas
MAX(número1; número2;...)
Devuelve el mayor valor de la lista de valores indicados.
MIN(número1; número2;...)
Devuelve el menor valor de la lista de valores indicados.
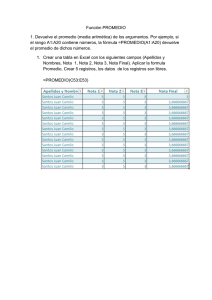
PROMEDIO(número1; número2;...)
Devuelve el promedio (media aritmética) de los argumentos.
Por ejemplo, si el rango A1:A20 contiene números, la fórmula PROMEDIO(A1:A20) devuelve el
promedio de dichos números. Si entre los argumentos hay celdas que contienen texto, valores lógicos o
que están vacías, estos valores se pasan por alto.
DESVEST(número1; número2;...) o DESVEST.M(número1; número2;...)
Calcula la desviación estándar de una muestra de acuerdo a la siguiente expresión:
∑
√
̅
, donde
̅ es el promedio de la muestra y N el tamaño de la muestra.
CONTAR(rango)
Cuenta cuántos números hay en el rango.
Por ejemplo, si en el rango A1:A20 hay solo 5 números CONTAR(A1:A20) da como resultado 5.
CONTAR.SI(rango; condición)
Cuenta el número de celdas dentro del rango que cumplen la condición dada. Por ejemplo
CONTAR.SI(B2:B15;">55") devuelve el número de celdas del rango B2:B15 que tienen un valor superior
a 55.
FRECUENCIA(datos; clases)
Devuelve una matriz vertical que representa la distribución de frecuencia de los datos.
En el ejemplo, en C2:C11 están los datos. En D2:D5 los límites superiores de las clases. Las clases son
los intervalos (-∞,2.2], (2.2,2.3], (2.3,2.4], (2.4,2.5] y (2.5, ∞). La función frecuencia se debe
introducir seleccionando las celdas E2:E6, donde aparecerán los resultados (en general una celda
más que las celdas que contienen las clases) y escribiendo =FRECUENCIA(C2:C11;D2:D5) en la
barra de funciones.
Se finaliza con CTRL+MAYÚS+ENTRAR
(CTRL+SHIFT+ENTER en los teclados en
inglés). Esta secuencia de teclas se debe usar
siempre para funciones que devuelven una matriz
y no un único valor. Si se finaliza de la manera
normal con ENTRAR sólo aparecerá un resultado
en la celda E2.
El resultado contenido en las celdas E2:E6
corresponde al número de ocurrencias de los
datos en cada clase.
DISTR.NORM(x; media; desv_estándar; acum) o DISTR.NORM.N(x; media; desv_estándar; acum)
Devuelve la distribución normal o gaussiana para la media y desviación estándar especificadas.




x es el valor donde se evalúa la función.
media es la media aritmética de la distribución.
desv_estándar es la desviación estándar de la distribución.
acum es un valor lógico que determina la forma de la función.
Para acum=FALSO, se calcula el valor de la función de densidad de probabilidad normal o
gaussiana:
,
donde  es la media y  la desviación estándar.
Para acum= VERDADERO, se calcula: ∫
ESTIMACION.LINEAL(conocido_y; conocido_x; constante; estadística)
Utiliza el método de cuadrados mínimos para calcular la línea recta que mejor describe los datos y
devuelve una matriz que describe la línea.
 conocido_y y conocido_x son los conjuntos de valores de y y de x vinculados por la relación y = a
x+b. Conviene disponerlos en columnas.
 constante es opcional. Si es VERDADERO o se omite, la ordenada al origen se calcula
normalmente. Si es FALSO, la ordenada al origen se establece como igual a cero.
 estadística es opcional. Si es FALSO o se omite solo devuelve el valor de pendiente y ordenada. Si
es VERDADERO devuelve también los errores de los parámetros del ajuste y otros datos estadísticos.
Como ESTIMACION.LINEAL devuelve una matriz se deben seleccionar previamente las celdas
donde aparecerán los resultados. En el caso de un ajuste lineal se deben seleccionar 5 filas x 2 columnas.
En el ejemplo siguiente se seleccionan las celdas F2:G6, se escribe en la barra de fórmulas
=ESTIMACION.LINEAL(B2:B9;A2:A9;VERDADERO;VERDADERO) y se finaliza con
CTRL+MAYÚS+ENTRAR. Esta secuencia de teclas es necesaria cuando una función da una matriz de
resultados. En la figura del ejemplo se muestran los resultados de la función (celdas F2:G6), se han
agregado carteles para indicar la ubicación de los resultados de interés. Las celdas F5, F6 y G6
contienen otros datos estadísticos que se emplean para analizar las bondades del ajuste.
Se puede usar ESTIMACION.LINEAL para ajustar los datos con un polinomio de grado n.
Por ejemplo,
ESTIMACION.LINEAL(A50:A58;B50:B58^{1;2;3};VERDADERO;VERDADERO) calcula el
polinomio de grado 3 y = a1 x + a2 x2 + a3 x3 + b que mejor ajusta los datos. En este caso la matriz
de resultados es de 5 filas x 4 columnas.
Funciones Trigonométricas
 SENO(angulo_r), COS(angulo_r), TAN(angulo_r)
Devuelven el seno, coseno y tangente de “angulo_r” respectivamente. Tanto para éstas como para
cualquier función trigonométrica, “angulo_r” debe estar dado en radianes. Para convertir un ángulo
dado en grados a radianes puede ser útil la función RADIANES(angulo_g) (ver más abajo), donde
“angulo_g” es el ángulo en grados. Así, si se quiere calcular el coseno de un ángulo, la forma de
hacerlo es:
COS(RADIANES(angulo_g)), si el ángulo se da en grados, o COS (angulo_r), si el ángulo se da en
radianes.
RADIANES(angulo_g)
Devuelve el valor en radianes de angulo_g, que es un ángulo dado en grados. Ej: RADIANES(180)= π
GRADOS(angulo_r)
Devuelve el valor en grados de angulo_r, que es un ángulo dado en radianes. Ej: GRADOS(π ) = 180
Herramientas de Análisis de Datos.
Excel también provee un complemento de Herramientas de Análisis de Datos. Para utilizarlo tiene que
estar activo. Para verificar que dicho complemento está activo ir a la pestaña Datos y ver que en el grupo
Análisis figura un ícono llamado Análisis de Datos. En caso de no encontrar el ícono se debe habilitar el
complemento mediante un procedimiento que varía según la versión de Excel.
Al elegir la opción “Análisis de Datos” aparece la siguiente ventana para acceder a las distintas
funciones:
“Estadística descriptiva” genera un informe estadístico de los datos de entrada: media, error estándar de
la media, mediana, moda, desviación estándar, varianza de la muestra, etc.
“Histograma” tabula y grafica la distribución en frecuencia para el rango de datos indicado. Si no se
ingresan las clases para agrupación de los datos Excel asigna una clasificación.
“Regresión” utiliza el método de cuadrados mínimos para ajustar una serie de pares de datos x,y con
una recta o un polinomio de grado mayor.
La siguiente tabla es un ejemplo de tabla de salida de la regresión. En la tabla se indican mediante
flechas los coeficientes del ajuste lineal con sus errores.