Revisión de las definiciones y métodos de estimación del Fill Rate

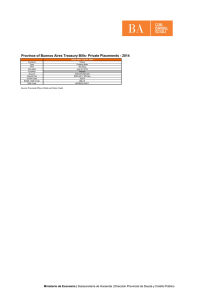
4th International Conference on Industrial Engineering and Industrial Management
XIV Congreso de Ingeniería de Organización
Donostia- San Sebastián , September 8th -10th 2010
Revisión de las definiciones y métodos de estimación del Fill Rate*
Ester Guijarro, Manuel Cardós, Eugenia Babiloni, Sofía Estellés Miguel1
1
Dpto. de Organización de Empresas. Universidad Politécnica de Valencia. Camino de Vera, s/n, 46022
Valencia. [email protected], [email protected], [email protected], [email protected]
Resumen
La fracción de la demanda satisfecha es una de las medidas del servicio al cliente más relevantes en la gestión
de inventarios. Por ello, existe una amplia literatura acerca de cómo estimarlo aunque el análisis de dicha
literatura revela que no hay consenso ni sobre su definición ni sobre el método de cálculo. En este artículo se
presenta una revisión de las definiciones y los métodos propuestos para calcular el fill rate y sus usos,
distinguiendo entre aquéllos que lo interpretan como una medida a corto plazo, y los que lo entienden como
medida a largo plazo.
Palabras clave: gestión de inventarios, fill rate.
1.
Introducción
La gestión de inventarios se ha convertido en un elemento clave dentro de la estrategia de
muchas industrias. De ella depende la consecución de objetivos importantes para la
organización, como es, entre otros, cumplir con un nivel de servicio al cliente previamente
determinado, manteniendo unos costes razonables para ello. A la hora de diseñar las políticas
de inventario, existen dos posibles estrategias: (1) minimizar los costes, o (2) minimizar el
inventario medio fijando un nivel de servicio mínimo. Algunos autores suponen que los costes
derivados de la escasez de existencias pueden expresarse de forma analítica sencilla, lo que
les permite centrarse en la minimización de los costes. En la práctica, sin embargo, estos
costes son difíciles de establecer y de estimar, por lo que se descartan a favor de un enfoque
centrado en la satisfacción de un nivel de servicio preestablecido.
El término ―servicio al cliente‖ se utiliza para describir la disponibilidad de los artículos
cuando son necesarios para el cliente (Fogarty et al. (1991)). Cuando la demanda es aleatoria,
la probabilidad de no poder satisfacer una parte de ésta con el stock disponible no puede
despreciarse (Silver et al. (1998)). No obstante, una organización debe procurar dar un nivel
de servicio adecuado y eventualmente elevado. Schneider (1978), Schneider (1981), Cohen y
Lee (1990), Lee y Billington (1992), Silver et al. (1998), Fogarty et al. (1991), Axsäter (2000)
presentan distintas métricas que permiten conocer y medir el nivel de servicio al cliente. Estas
métricas se emplean en control de inventarios con dos finalidades principales: (1) analizar el
rendimiento de los sistemas de gestión de inventarios, y (2) establecer los parámetros de las
políticas de inventarios.
Fogarty et al. (1991) dividen las medidas de servicio en dos tipos: las porcentuales y las
medidas de valor absoluto, aconsejando compararlas con un estándar previamente establecido.
Silver et al. (1998) establecen cuatro métricas fundamentales de nivel de servicio al cliente: (i)
el nivel de servicio de ciclo (CSL) que indica el porcentaje de ciclos en los que no existen
*
Este trabajo forma parte del proyecto GEMA financiado por el Ministerio de Educación y Ciencia, Ref. DPI
2007-65441
1320
roturas de stock, también conocido como P1; (ii) El fill rate (FR) que se define como la
fracción de demanda que se cubre con el stock físico disponible o P2; (iii) El ready rate o
fracción de tiempo durante el cual el stock neto es positivo, también conocido como P3; y (iv)
el TBS o tiempo medio entre roturas de stock; siendo el nivel de servicio de ciclo (CSL) y el
fill rate las más empleadas y desarrolladas. Este artículo se centra en el fill rate cuya
definición como en (ii) ha sido interpretada de distintas formas en la literatura. En el presente
trabajo se realiza una revisión de las principales definiciones y métodos de estimación que
aparecen en la literatura (Sección 2). Dentro de este revisión, se distingue entre aquellos
autores que estiman el fill rate a corto plazo, es decir, considerando la demanda satisfecha en
cada periodo (Sección 2.1); y aquellos que lo calculan como medida a largo plazo, teniendo
en cuenta la demanda cubierta en un plazo de tiempo determinado (Sección 2.2). Por último,
las conclusiones y potenciales líneas de investigación se resumen en la Sección 3.
2.
El Fill Rate y los horizontes temporales
FILL RATE
Fill Rate a largo plazo
Fracción de demanda
cubierta con el stock físico
disponible en un periodo de
tiempo determinado
Aproximación tradicional
Hadley y Whitin 1963
Silver y Petersson 1985
Johnson et al. 1995
Schneider 1978
Schneider 1981
Tijm y Gronevelt 1984
Asxäter 2000
Cohen et al. 1988
Zipkin 2000
Tempelmeier 2007
Moors y Strijbosch 2002
Chopra y Meidln 2004
Guijarro et al. 2010
Método exacto
Fill Rate a corto plazo
Fracción de demanda por
ciclo cubierta con el stock
físico disponible
Feeney y Sherbrooke 1966
Muchstadt y Thomas 1980
Boyaci y Gallego 2001
Guijarro et al. 2010
Para (R, S) y distribución
Normal
Determinación de
parámetros de la política s.a.
un nivel de fill rate
Axsäter 2003
Chen 2003
Bollapragada y Zhang 2003
Sobel 2004
Kwon 2006
Zhang yZhang 2007
Teunter 2009
Minimización costes de
inventario s.a. un nivel de
fill rate
Para Gamma
Para (s, Q) y Normal
Para (R, S)
Para Poisson Compuesta
Para Poisson
Para Poisson
Para (R, S)
Figura 17: Revisión de la literatura sobre usos y métodos de estimación del fill rate. [Elaboración propia]
La definición y estimación de fill rate han sido estudiadas ampliamente tanto en el ámbito
práctico como en la literatura sobre la gestión de operaciones en los últimos sesenta años. No
obstante, su definición resulta ambigua, puesto que no se especifica el periodo temporal al que
se refiere, lo que provoca distintas interpretaciones de la misma definición. En este sentido
Silver et al. (1998) sugieren dos posibles generalizaciones del fill rate, una que considera la
1321
fracción de demanda satisfecha en cada periodo, y otra que analiza la fracción de demanda
que debe atenderse con el stock físico disponible en un plazo determinado de tiempo, es decir,
como medida a largo plazo. Por tanto, la definición del fill rate pueden concretarse según el
horizonte temporal considerado: a corto plazo (c/p) y a largo plazo (l/p). La interpretación del
fill rate a corto plazo ha generado un mayor número de aportaciones, aunque en los últimos
años, la generalización a largo plazo ha suscitado un interés creciente en la comunidad
científica. La sección 2.1 y Sección 2.2 se dedican a la generalización del fill rate a c/p y a l/p
respectivamente.
2.1. El Fill Rate a corto plazo
El fill rate se define como el porcentaje de demanda que se atiende con el stock que hay en la
estantería, sin incurrir en pérdida de ventas ni retrasos en los pedidos (Hadley y Whitin
(1963), Silver et al. (1998), Axsäter (2000), Chopra y Meindl (2004)). Siguiendo esta
definición, el FR puede expresarse como:
Fill Rate=E(
demanda satisfecha con el stock físico
)
demanda total
(1)
Esta definición no especifica el plazo temporal al que se refiere, sin embargo, para derivar un
método de cálculo del fill rate, muchos son los autores que determinan dicho periodo
temporal tomando la demanda de un ciclo, de modo que, en la práctica, calculan el fill rate
para un ciclo, i.e. a corto plazo.
Johnson et al. (1995) presentan una revisión exhaustiva de las definiciones y estimaciones del
fill rate. Tal y como señalan, en la mayoría de los trabajos, el fill rate se estima mediante la
denominada aproximación tradicional, en lugar de utilizar la expresión (1). Esta aproximación
examina el número de unidades demandadas que no pueden ser atendidas, en vez de examinar
directamente la demanda satisfecha. Según esto, la aproximación tradicional del fill rate
puede expresarse como el complementario del ratio entre la demanda esperada no satisfecha
por ciclo y la demanda total esperada, es decir:
Fill RateAprox
1
E (demanda no satisfecha por ciclo)
E (demanda total por ciclo)
(2)
Dicha aproximación tradicional y los métodos aproximados basados en ella propuestos por
diversos autores para estimar el fill rate aparecen en prácticamente todos los libros de
dirección de operaciones (por ejemplo, Silver et al. (1998)), Axsäter (2000), Cohen et al.
(1988); Zipkin (2000), Chopra y Meindl (2004)), y han sido ampliamente empleados en
industria. A pesar de que estas expresiones tradicionales son relativamente simples, tienen la
limitación de no expresar el fill rate de forma exacta. Como demuestran los trabajos de
Johnson et al. (1995) y Guijarro et al. (2010), calcular el fill rate con la expresión (2) lleva a
subestimar su verdadero valor, lo que tiene importantes implicaciones para el sistema de
gestión de inventarios, sobre todo si el fill rate se utiliza para determinar los parámetros de la
política de inventario.
En las siguientes subsecciones se presenta una revisión de los artículos dedicados al cálculo
del fill rate a corto plazo, distinguiendo aquellos autores que proponen métodos de estimación
basados en la aproximación tradicional (expresión (2)), y aquellos que desarrollan expresiones
exactas para determinar el fill rate en determinadas políticas de inventario y/o distribuciones
de demanda.
1322
2.1.1 Métodos basados en la aproximación tradicional para calcular el fill rate a corto
plazo
A pesar de la subestimación que se obtienen del valor del fill rate cuando se utiliza la
aproximación tradicional para su obtención, existe una amplia literatura que se centra en
desarrollar métodos de estimación para la expresión (2) para distintas políticas de gestión de
inventarios y, más concretamente, para estimar la demanda esperada no cubierta con el stock
físico en cada ciclo, i.e. E(demanda no satisfecha por ciclo).
Unos de los primeros autores que hablan del fill rate y proponen una aproximación para el
cálculo de la escasez esperada son Hadley y Whitin (1963). En su libro, presentan una
expresión del fill rate cuando la demanda sigue una distribución de Poisson, que luego
extienden al caso de la distribución Normal, cuando el inventario es gestionado mediante una
política de revisión periódica (R, S). En esta expresión calculan la escasez esperada como la
diferencia entre las órdenes atrasadas en el momento t+R+L menos los pedidos pendientes en
el momento t+L. Tal y como indican Johnson et al. (1995), esta aproximación subestima
consistentemente el verdadero valor del fill rate como consecuencia del doble recuento que se
produce de las unidades no servidas en el periodo anterior. En revisión periódica, se produce
una situación de escasez cuando la demanda total de un periodo excede el valor del stock de
referencia. Si en un periodo i, se produce esta situación, la demanda no satisfecha debe
retrasarse al periodo siguiente, i+1. Si en este nuevo periodo la orden de reaprovisionamiento
recibida no es suficientemente grande para satisfacerla, de nuevo se retrasa la demanda al
periodo i+2. Este doble recuento provoca una sobreestimación de la escasez, y en
consecuencia, una subestimación del valor del fill rate.
Silver y Peterson (1985) también reconoció que la expresión tradicional del fill rate no era
exacta debido a este doble recuento de la demanda pendiente de los periodos anteriores. Para
superar este problema, desarrollan una expresión mejorada de la presentada en Silver (1970)
para el caso de los sistemas de inventarios revisados de forma continua y que posteriormente
extienden al caso de revisión periódica. Pero como indican Johnson et al. (1995) esta
expresión tampoco resulta un cálculo exacto del FR ya que asume que en cada periodo de
revisión se ordenan exactamente Q unidades, cuando en las políticas de revisión periódica el
tamaño de las órdenes varía de un periodo a otro en función de la demanda del periodo, que es
estocástica.
Con la intención de superar el inconveniente del doble recuento, Johnson et al. (1995)
proponen un nuevo método exacto para calcular el número esperado de unidades demandadas
no satisfechas en un periodo cuando la demanda sigue una distribución Normal y el inventario
utiliza una política de revisión periódica. Sin embargo, todos estas aproximaciones sufren del
mismo problema de subestimación del FR, ya no tanto por el efecto de las unidades atrasadas,
sino por el hecho de calcularlo a partir de la aproximación tradicional en lugar de tal y como
se define, i.e., según la expresión (1).
Otro conjunto de autores (Schneider (1978), Schneider (1981) y Tijms y Groenevelt (1984),
Axsäter (2000)) presentan métodos de aproximación para el cálculo del fill rate, que utilizan
como restricción para determinar los parámetros de la política. En concreto, desarrollan
métodos de cálculo para la expresión (2) que emplean para determinar el valor del punto de
pedido, tomando un determinado valor del fill rate como restricción. A la hora de determinar
un punto de pedido adecuado, pueden utilizarse bien restricciones sobre el nivel de servicio al
cliente deseado, o bien basarse en los costes de escasez o pedidos pendientes. En la práctica,
no obstante, suele ser más fácil especificar un determinado nivel de servicio (Axsäter (2000)).
Basándose en esto, los trabajos de Schneider (1978) y Schneider (1981) presentan unas
aproximaciones para establecer el punto de pedido de al política dado un nivel de servicio
1323
determinado y con un tamaño de orden preestablecido. Tijms y Groenevelt (1984) extienden
este trabajo, desarrollando un modelo para el sistema de inventario (s, S), tanto en revisión
periódica como en continua, cuando existen pedidos pendientes. Además, presentan
aproximaciones obtenidas mediante el ajuste de las distribuciones de demanda hacia las
distribuciones Gamma y Normal, respectivamente. Este modelo se basa en el análisis
aproximado del proceso de renovación de la llegada de los pedidos de reposición,
considerando un sistema de inventario estocástico en el que la secuencia de los momentos en
los que se produce demanda puede describirse bajo un proceso de renovación. Años más
tarde, Axsäter (2000) explica cómo determinar el punto de pedido dado un fill rate objetivo
cuando el inventario es gestionado con una política de revisión continua (s, Q). En este
desarrollo, plantea una expresión analítica para una demanda con distribución de Poisson
compuesta que sólo resulta exacta si se cumple que: (i) no existe posibilidad de tener
demanda nula en el ciclo, y (ii) el nivel de inventario tampoco puede ser igual a cero. A partir
de esta expresión, propone una aproximación para el caso de la distribución Normal, que no
es exacta ya que desprecia el efecto de los undershoots (desviaciones en el punto de pedido).
Es bastante común en la práctica utilizar un determinado valor de fill rate objetivo como
restricción para minimizar los costes de inventarios, lo cual ha generado una extensa literatura
sobre distintos modelos de optimización de costes sujetos a un nivel determinado de servicio
al cliente. Cohen et al. (1988) presentan un modelo para un sistema de inventario de revisión
periódica (s, S) donde existen dos clases de prioridad de la demanda: el stock es utilizado en
primer lugar para satisfacer la demanda de alta prioridad, y el resto está entonces disponible
para cubrir la demanda de baja prioridad. En este trabajo, los autores proponen un modelo
aproximado del fill rate para un sistema de ventas perdidas y evalúan su solución algorítmica
para resolver el problema de optimización de costes con restricciones de niveles de servicio.
Cohen et al. (1988); Zipkin (2000) desarrolla también un modelo de minimización de costes
para el caso de distribución de demanda con Poisson compuesta. Más recientemente,
Tempelmeier (2007) formula un modelo que minimiza los costes de instalación y de
explotación en un sistema de revisión periódica dado un valor objetivo de FR, que mide con
la probabilidad de que el inventario al final de cada periodo se convierta en negativo, y
alternativamente, con la probabilidad de que la demanda se cubra con el stock físico
disponible. En este trabajo, se asume que los niveles de servicio son suficientemente grandes
como para asegurar que el inventario neto será una buena aproximación de las existencias
disponibles.
Por otro lado, otro conjunto de autores han desarrollado distintos métodos de cálculo de la
aproximación tradicional en condiciones específicas, bien para determinadas distribuciones de
demanda, o bien para determinados modelos de gestión del inventario. En su artículo, Moors
y Strijbosch (2002) presentan un método de cálculo exacto del fill rate, basado en la expresión
(2), y que particularizan para el caso de que la demanda siga una distribución Gamma, el
inventario se gestione con una política híbrida (R, s, S) y el leadtime sea constante. Hasta
entonces, se habían propuesto diversas aproximaciones del fill rate derivadas,
fundamentalmente, de la teoría de renovación y sujetas a condiciones específicas, como que la
diferencia entre el stock de referencia y el punto de pedido (S – s) debía ser suficientemente
grande en comparación con la media de la demanda en el periodo de revisión. En este trabajo,
se presenta también una comparativa entre la expresión del fill rate propuesta por Tijms y
Groenevelt (1984) y el método exacto de los autores, donde se demuestra que la aproximación
de los primeros, para una distribución de demanda Gamma, es satisfactoria para el caso de
niveles altos de servicio al cliente.
Chopra y Meindl (2004) desarrollan una expresión para el cálculo de la aproximación
tradicional del fill rate presentando un método de cálculo de la escasez esperada por ciclo de
1324
reaprovisionamiento, pero a diferencia de Hadley y Whitin (1963), Silver y Peterson (1985) o
Johnson et al. (1995), lo hacen para el caso de que el sistema esté gestionado con una política
de revisión continua (s, Q) y la demanda siga una distribución Normal. Además, utilizan esta
expresión para evaluar el stock de seguridad del sistema dado un determinado nivel de fill
rate.
Guijarro et al. (2010) proponen un método de cálculo exacto de la aproximación tradicional
para cualquier distribución de demanda en revisión periódica, (R, S). Pero a diferencia de
todos los autores anteriores, en lugar de calcular el valor esperado de las unidades no servidas,
analizan la aproximación tradicional desde la óptica de las unidades demandas servidas, de
forma que la expresión (2) puede reescribirse como sigue:
E (demanda satisfecha por ciclo)
E (demanda total por ciclo)
Fill RateAprox
(3)
2.1.2 Métodos exactos para la obtención del fill rate a corto plazo
Pocos son los trabajos en los que se presenta un método de cálculo exacto del fill rate basado
en su propia definición (fracción de demanda satisfecha directamente con el stock físico
disponible). Uno de los primeros artículos es el de Feeney (1966), quienes desarrollan un
método exacto para calcular el FR a través de las probabilidades estacionarias de las unidades
de reabastecimiento para una política (S-1, S). En su desarrollo, asumen que la demanda sigue
una distribución de Poisson compuesta Muckstadt (1980) siguen este mismo planteamiento en
un sistema single-echelon cuando la distribución de la demanda es Poisson y simplifican la
expresión desarrollada por Feeney (1966), obteniendo una formulación mucho más sencilla.
Otro trabajo donde se presenta un método de cálculo del fill rate que no utiliza la
aproximación tradicional es el de Boyaci y Gallego (2001), quienes presentan un modelo de
minimización de costes sujetos a una restricción del fill rate para una cadena de suministro
multiescalón cuando la demanda sigue una distribución de Poisson. Pero en este trabajo,
definen el fill rate como la ―probabilidad límite de tener inventario físico positivo en el último
escalón‖, definición que no se ajusta al concepto estándar del fill rate, y que en realidad
podría entenderse como la probabilidad de que no ocurra una rotura de stock, es decir, el
CSL.
Recientemente, Guijarro et al. (2010) proponen un método de cálculo exacto de la expresión
(1) del FR basándose en el cálculo de la demanda satisfecha en el ciclo. Esta expresión es
válida para cualquier tipo de distribución discreta de la demanda. En ella, se especifica el
periodo temporal, tomando el ciclo, y se desprecian aquéllos en los que la demanda es nula.
2.2. El Fill Rate a largo plazo
Tal y como se ha indicado, existe una segunda generalización del fill rate que considera la
demanda que debe atenderse con el stock disponible a largo plazo, y propone una nueva
definición del FR, entendiéndolo como la media de la demanda a largo plazo que se cubre con
el stock disponible en la estantería y que puede expresarse de la siguiente manera:
Fill Ratel / p
lim E (
t
demanda satisfecha con el stock físico en t periodos
)
demanda total en t periodos
(4)
Esta generalización ha sido menos estudiada en la gestión de inventarios, sin embargo, en los
últimos diez años han aparecido trabajos que presentan métodos de cálculo para la expresión
(4) Chen et al. (2003), a pesar de definir el fill rate sin determinar el espacio temporal,
analizan el efecto del horizonte finito a largo plazo en el valor esperado del FR y proponen
una expresión del fill rate en un sistema gestionado con revisión periódica, horizonte finito y
1325
una distribución de demanda no específica. A partir de los resultados de su trabajo, concluyen
que si se utiliza la expresión de horizonte infinito en un sistema de inventario de horizonte
finito para establecer los niveles de inventario, podrán alcanzarse mayores niveles de fill rate
que los deseados, pero se incurrirá en mayores costes de inventario que los necesarios.
En Axsäter (2003) se aborda el problema de la minimización de costes de inventario sujeto a
alcanzar un determinado valor del fill rate en revisión continua y distribución de demanda
Poisson compuesta. En este trabajo, el fill rate se define a largo plazo, como en (4).
Posteriormente, siguiendo esta misma definición, Sobel (2004) presenta un método de cálculo
exacto del fill rate cuando la demanda se distribuye con una función de distribución Normal y
con una función de distribución Gamma y el inventario se revisa con política periódica. Dado
que las expresiones exactas que el autor deriva son complejas, en el mismo trabajo se
proponen fórmulas aproximadas únicamente para la distribución Normal.
Utilizando las fórmulas derivadas en Sobel (2004), Kwon et al. (2006) examina el problema
de la minimización de costes de inventarios sujeto a un nivel de servicio al cliente, cuando la
demanda sigue un proceso de distribución Normal y el sistema de inventario es en serie. Poco
más tarde, Zhang y Zhang (2007) amplían las fórmulas de Sobel (2004), y presentan un
método de cálculo del fill rate para cualquier distribución de demanda, trabajo que es revisado
en detalle por Teunter (2009).
3.
Conclusiones y futuras líneas de investigación
En este artículo se presenta una revisión detallada del fill rate, una de las métricas de servicio
al cliente más utilizada en la gestión de inventarios. A pesar de que existe una amplia
literatura sobre ella, no hay un consenso ni sobre su definición ni sobre los métodos para su
estimación. La mayoría de los autores proponen métodos de cálculo aproximados, utilizando
la aproximación tradicional (expresión (2)). Por otro lado, la definición de esta métrica resulta
ambigua, al no concretar el periodo temporal al que se refiere, lo que ha motivado que los
diferentes autores interpreten el concepto de fill rate de dos maneras distintas, bien a corto
plazo, tomando la demanda satisfecha por ciclo; o bien como una medida de servicio a largo
plazo. Por tanto, puede concluirse que el fill rate es, en realidad, una familia de métricas que
se diferencian entre sí según el periodo temporal al que se refieran. Las líneas de
investigación futuras se deberían centrar en proponer métodos de estimación exactos del fill
rate aplicables a cualquier patrón de demanda, para las distintas políticas de gestión.
Agradecimientos
Este trabajo forma parte del proyecto GEMA financiado por el Ministerio de Educación y
Ciencia, Ref. DPI 2007-65441.
Referencias
Axsäter, S. (2000). Inventory Control. Kuwer Academic Publishers.
Axsäter, S. (2003). Note: Optimal Policies for Serial Inventory Systems Under Fill Rate
Constraints. Management Science, Vol. 49, No 2, pp. 247-253.
Bollapragada, R. (2004). Managing two-stage serial inventory systems under demand and
supply uncertainty and customer service level requirements.
1326
Boyaci, T.; Gallego, G. (2001). Serial Production/Distribution Systems Under Service
Constraints. Manufacturing Service Operations Management, Vol. 3, No 1, pp. 43-50.
Chen, J.H.; Lin, D.K.J.; Thomas, D.J. (2003). On the single item fill rate for a finite horizon.
Operations Research Letters, Vol. 31, No 2, pp. 119-123.
Chopra, S.; Meindl, P. (2004). Supply Chain Management. 2nd Editionth ed. Pearson. Prentice
Hall.
Cohen, M.A.; Kleindorfer, P.R.; Lee, H.L. (1988). Service Constrained (S, S) Inventory
Systems with Priority Demand Classes and Lost Sales. Management Science, Vol. 34, No 4,
pp. 482-499.
Cohen, M.A.; Lee, H.L. (1990). Out of Touch with Customer Needs - Spare Parts and After
Sales Service. Sloan Management Review, Vol. 31, No 2, pp. 55-66.
Feeney, G.J. (1966). The (S-1,S) inventory policy under compound Poisson demand.
Fogarty, D.W.; Blackstone, J.H.; Hoffman, T.R. (1991). Production and Inventory
Management. Second Editionth ed. South-Western Publishing Co.
Guijarro, E.; Babiloni, E.; Cardós, M. (2010). An exact calculation of the fill rate in a periodic
review inventory policy. 16th International Working Seminar on Production Economics.
Hadley, G.; Whitin, T. (1963). Analysis of Inventory Systems. Prentice-Hall.
Johnson, M.E.; Lee, H.L.; Davis, T.; Hall, R. (1995). Expressions for Item Fill Rates in
Periodic Inventory Systems. Naval Research Logistics, Vol. 42, No 1, pp. 57-80.
Kwon, I.H.; Kim, S.S.; Baek, J.G. (2006). A simulation based heuristic for serial inventory
systems under fill-rate constraints. International Journal of Advanced Manufacturing
Technology, Vol. 31, No 3-4, pp. 297-304.
Lee, H.L.; Billington, C. (1992). Managing Supply Chain Inventory - Pitfalls and
Opportunities. Sloan Management Review, Vol. 33, No 3, pp. 65-73.
Moors, J.J.A.; Strijbosch, L.W.G. (2002). Exact fill rates for (R, s, S) inventory control with
gamma distributed demand. Journal of the Operational Research Society, Vol. 53, No 11, pp.
1268-1274.
Muckstadt, J.A. (1980). Are Multi-Echelon Inventory Methods Worth Implementing in
Systems with Low-Demand-Rate Items.
Schneider, H. (1978). Methods for Determining Re-Order Point of An (S,S) Ordering Policy
When A Service Level Is Specified. Journal of the Operational Research Society, Vol. 29, No
12, pp. 1181-1193.
Schneider, H. (1981). Effect of service-levels on order-points or order-levels in inventory
models. International Journal of Production Research, Vol. 19, No 6, pp. 615-631.
Silver, E.A.; Peterson, R. (1985). Decisions system for inventory management and production
planning. 2ndth ed. John Wiley & Sons.
1327
Silver, E.A.; Pyke, D.F.; Peterson, R. (1998). Inventory Management and Production
Planning and Scheduling. 3ªth ed. Wiley.
Silver, E.A. (1970). A Modified Formula for Calculating Customer Service Under Continuous
Inventory Review. AIIE Transactions, Vol. 2, No 3, pp. 241-245.
Sobel, M.J. (2004). Fill Rates of Single-Stage and Multistage Supply Systems. Manufacturing
& Service Operations Management, Vol. 6, No 1, pp. 41-52.
Tempelmeier, H. (2007). On the stochastic uncapacitated dynamic single-item lotsizing
problem with service level constraints. European Journal of Operational Research, Vol. 181,
No 1, pp. 184-194.
Teunter, R.H. (2009). Note on the fill rate of single-stage general periodic review inventory
systems. Operations Research Letters, Vol. 37, No 1, pp. 67-68.
Tijms, H.C.; Groenevelt, H. (1984). Simple Approximations for the Reorder Point in Periodic
and Continuous Review (S,S) Inventory Systems with Service Level Constraints
38. European Journal of Operational Research, Vol. 17, No 2, pp. 175-190.
Zhang, J.; Zhang, J. (2007). Fill rate of single-stage general periodic review inventory
systems. Operations Research Letters, Vol. 35, No 4, pp. 503-509.
Zipkin, P.H. (2000). Foundations of Inventory Management. McGraw-Hill Higher Education.
1328