teorema de casey

TEOREMA DE CASEY
Gustavo Ríos
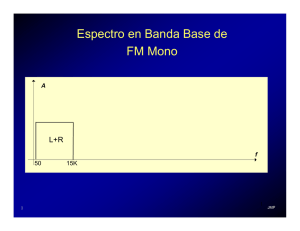
La deferencia de potencias de un punto respecto a dos circunferencias es igual al doble del producto de la
distancia de dicho punto al eje radical de las circunferencias y la distancia entre sus centros.
P
O1
O2
J
H
e
Demostración
Sean H la proyección ortogonal de P en la recta O1O2 y {J } = OO1 ∩ e . Se observa:
2
2
2
J ∈ e ⇒ JO2 − r22 = JO1 − r12 ⇒ r22 − r12 = JO2 − JO1
2
2
2
2
H pie de altura [PH ] en UO1PO2 ⇒ PO2 − PO1 = HO2 − HO1
2
Sea δ la diferencia de las potencias de P con respecto a las circunferencias
(
= (PO
2
) (
− PO ) − (r
2
δ = PO2 − r22 − PO1 − r12
2
2
2
2
2
2 − r1
1
)
)
Combinando las relaciones observadas al principio con la expresión de δ se obtiene
(
= (HO
2
) (
) − (HO
2
2
δ = HO2 − HO1 − JO2 − JO1
2
2
− JO2
2
1
2
− JO1
2
2
)
)
= (HO2 − JO2 )(HO2 + JO2 ) − (HO1 − JO1 )(HO1 + JO1 )
= (HJ )(HO2 + JO2 ) − (−HJ )(HO1 + JO1 )
(
)
(
)
= HJ (HO2 + JO2 ) + (HO1 + JO1 )
= HJ (HO2 + HO1 ) + (JO2 + JO1 )
= HJ (2 O1O2 )
= 2 O1O2 HJ
Como PH ⊥ O1O2 ∧ e ⊥ O1O2 , resulta dist (P , e ) = dist (H , e ) = HJ . Por lo tanto δ = 2 O1O2 dist (P , e ) . LQQD.