construcción geométrica de las funciones

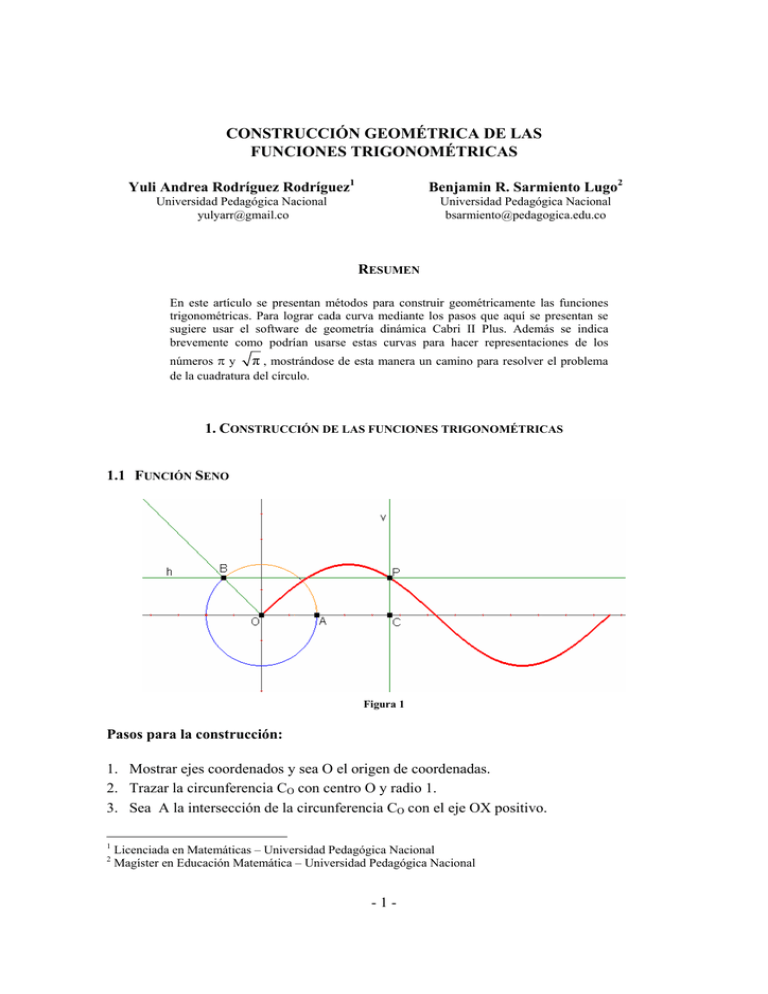
CONSTRUCCIÓN GEOMÉTRICA DE LAS
FUNCIONES TRIGONOMÉTRICAS
Yuli Andrea Rodríguez Rodríguez1
Benjamin R. Sarmiento Lugo2
Universidad Pedagógica Nacional
[email protected]
Universidad Pedagógica Nacional
[email protected]
RESUMEN
En este artículo se presentan métodos para construir geométricamente las funciones
trigonométricas. Para lograr cada curva mediante los pasos que aquí se presentan se
sugiere usar el software de geometría dinámica Cabri II Plus. Además se indica
brevemente como podrían usarse estas curvas para hacer representaciones de los
números π y π , mostrándose de esta manera un camino para resolver el problema
de la cuadratura del círculo.
1. CONSTRUCCIÓN DE LAS FUNCIONES TRIGONOMÉTRICAS
1.1 FUNCIÓN SENO
Figura 1
Pasos para la construcción:
1. Mostrar ejes coordenados y sea O el origen de coordenadas.
2. Trazar la circunferencia CO con centro O y radio 1.
3. Sea A la intersección de la circunferencia CO con el eje OX positivo.
1
2
Licenciada en Matemáticas – Universidad Pedagógica Nacional
Magíster en Educación Matemática – Universidad Pedagógica Nacional
-1-
Sea B un punto sobre la circunferencia CA.
Trazar el arco AB.
Sea m la medida del arco AB.
Trazar la recta h perpendicular al eje Y y que pase por B.
Transferir la medida m sobre el eje OX positivo. Sea C el punto donde termina la
transferencia.
9. Trazar la recta v perpendicular al eje X que pase por C.
10. Sea P punto de intersección entre las rectas h y v.
11. El lugar geométrico generado por P cuando se mueve B sobre la circunferencia CO es la
función Seno.
4.
5.
6.
7.
8.
1.2 FUNCIÓN COSENO
Figura 2
Pasos para la construcción:
1. Mostrar ejes coordenados y sea O el origen de coordenadas.
2. Trazar la circunferencia CO con centro O y radio 1.
3. Sea B un punto sobre la circunferencia CO.
4. Sea A la intersección de la circunferencia CO con el eje OX positivo.
5. Trazar el arco AB.
6. Sea m la medida del arco AB.
7. Transferir la media m sobre el eje OX positivo. Sea C el punto donde termina la
transferencia.
8. Trazar la recta v perpendicular al eje X y que pase por B.
9. Sea D la intersección de la recta v con el eje X.
-2-
10. Sea X1 la abscisa de las coordenadas del punto D.
11. Transferir X1 sobre el eje Y. Sea E el punto donde termina ésta transferencia.
12. Trazar la recta h perpendicular al eje Y y que pase por E.
13. Trazar la recta n perpendicular al eje X y que pase por C.
14. Sea P la intersección entre las rectas n y h.
15. El lugar geométrico generado por P cuando se mueve B sobre la circunferencia CO es la
función Coseno.
1.3 FUNCIÓN TANGENTE
Figura 3
Pasos para la construcción:
1.
2.
3.
4.
5.
6.
7.
Mostrar ejes coordenados y sea O el origen de coordenadas.
Trazar la circunferencia CO con centro O y radio 1.
Sea A la intersección de la circunferencia CO con el eje OX positivo.
Sea B un punto sobre la circunferencia CO.
Trazar el arco AB.
Sea m la medida del arco AB.
Transferir la media m sobre el eje OX positivo. Sea C el punto donde termina la
transferencia.
-3-
8. Trazar la recta l perpendicular al eje X y que pase por A.
9. Trazar la recta OB.
10. Sea D la intersección de la recta OB con la recta l.
11. Trazar la recta s perpendicular al eje Y y que pase por D.
12. . Trazar la recta n perpendicular al eje X y que pase por C.
13. Sea P la intersección entre las rectas s y n.
14. El lugar geométrico generado por P cuando se mueve B sobre la circunferencia CO es la
función Tangente.
1.4 FUNCIÓN COTANGENTE
Figura 4
Pasos para la construcción:
1.
2.
3.
4.
5.
6.
7.
Mostrar ejes coordenados y sea O el origen de coordenadas.
Trazar la circunferencia CO con centro O y radio 1.
Sea A la intersección de la circunferencia CO con el eje OX positivo.
Sea B un punto sobre la circunferencia CO.
Trazar el arco AB.
Sea m la medida del arco AB.
Transferir la media m sobre el eje OX positivo. Sea C el punto donde termina la
transferencia.
-4-
8. Trazar la recta l perpendicular al eje X y que pase por A.
9. Trazar la recta OB.
10. Sea D la intersección de la recta OB con la recta l.
11. Trazar la recta s perpendicular al eje Y y que pase por D.
12. Sea E la intersección de la recta s con el eje Y.
13. Sea G el inverso del punto E con respecto a la circunferencia CO.
14. Trazar la recta r perpendicular al eje Y y que pase por G.
15. Trazar la recta n perpendicular al eje X y que pase por C.
16. Sea P la intersección entre las rectas r y n.
17. El lugar geométrico generado por P cuando se mueve B sobre la circunferencia CO es la
función Cotangente.
1.5 FUNCIÓN SECANTE
Figura 5
Pasos para la construcción:
1. Mostrar ejes coordenados y sea O el origen de coordenadas.
2. Trazar la circunferencia CO con centro O y radio 1.
-5-
3. Sea B un punto sobre la circunferencia CO.
4. Sea A la intersección de la circunferencia CO con el eje OX positivo.
5. Trazar la recta OB.
6. Trazar el arco AB.
7. Sea m la medida del arco AB.
8. Transferir la media m sobre el eje OX positivo. Sea E el punto donde termina la
transferencia.
9. Trazar la recta l perpendicular a la recta OB y que pase por B.
10. Sea C la intersección de la recta l con el eje X.
11. Sea X1 la abscisa de las coordenadas del punto C.
12. Transferir X1 sobre el eje Y. Sea D el punto donde termina ésta transferencia.
13. Trazar la recta n perpendicular al eje Y y que pase por D.
14. Trazar la recta s perpendicular al eje X y que pase por E.
15. Sea P la intersección entre las rectas n y s.
16. El lugar geométrico generado por P cuando se mueve B sobre la circunferencia CO es la
función Secante.
1.6 FUNCIÓN COSECANTE
Figura 6
-6-
Pasos para la construcción:
1. Mostrar ejes coordenados y sea O el origen de coordenadas.
2. Trazar la circunferencia CO con centro O y radio 1.
3. Sea A la intersección de la circunferencia CO con el eje OX positivo.
4. Sea B un punto sobre la circunferencia CA.
5. Trazar el arco AB.
6. Sea m la medida del arco AB.
7. Trazar la recta h perpendicular al eje Y y que pase por B.
8. Sea D la intersección de la recta h con el eje Y.
9. Sea E el inverso de D con respecto a la circunferencia CO.
10. Trazar la recta s perpendicular al eje Y y que pase por E.
11. Transferir la medida m sobre el eje OX positivo. Sea C el punto donde termina la
transferencia.
12. Trazar la recta v perpendicular al eje X que pase por C.
13. Sea P punto de intersección entre las rectas s y v.
14. El lugar geométrico generado por P cuando se mueve B sobre la circunferencia CO es la
función Cosecante.
2. USO EN REPRESENTACIÓN
DE NÚMEROS TRASCENDENTES
Usando las funciones trigonométricas se pueden obtener representaciones del número π
sobre el eje X y representaciones del número π construyendo la media geométrica entre π
y el radio 1 de la circunferencia goniométrica.
2.1 USO DE LA FUNCIÓN SENO
1. Ocultar la semirrecta OB y las rectas h y v.
2. Sean D y E las intersecciones del lugar geométrico con el eje OX positivo.
Se puede observar que los puntos P y C se encuentran en D cuando el arco AB coincide con
la semicircunferencia; como la longitud del segmento OD es igual a la longitud del arco AB
se infiere que la longitud del segmento OD es igual a π, que es la longitud de la
semicircunferencia de radio 1.
3. Sea M el punto medio del segmento OD.
4. Trazar la circunferencia CM con centro M y radio OM.
5. Trazar la recta s perpendicular al eje X y que pase por A.
6. Sean R y T las intersecciones de la circunferencia CM con la recta s.
7. La longitud del segmento AT es igual a π .
-7-
Figura 7
2.2 USO DE LA FUNCIÓN COSENO
Como el segmento AD mide π y el segmento OA mide 1, entonces el segmento AG
mide π por ser media geométrica de OA y AD.
Figura 8
2.3 USO DE LA FUNCIÓN TANGENTE
Como el segmento OF mide π y el segmento EO mide 1, entonces el segmento OG
mide π por ser media geométrica de EO y OF.
-8-
Figura 9
2.4 USO DE LA FUNCIÓN COTANGENTE
Como el segmento AF mide π y el segmento OA mide 1, entonces el segmento AG
mide π por ser media geométrica de OA y AF.
Figura 10
-9-
2.5 USO DE LA FUNCIÓN SECANTE
Como el segmento OE mide π y el segmento FO mide 1, entonces el segmento OG
mide π por ser media geométrica de FO y OE.
Figura 11
2.6 USO DE LA FUNCIÓN COSECANTE
Como el segmento OF mide π y el segmento DO mide 1, entonces el segmento OG
mide π por ser media geométrica de OF y DO.
Figura 12
- 10 -
REFERENCIAS BIBLIOGRÁFICAS
Arguedas, Jendry. Construcción de lugares geométricos trascendentales y su importancia en
la enseñanza de la matemática. (V Congreso de enseñanza de la matemática asistica por
computadora).
Álvarez, J. (2006), Curvas en la historia. España. Nivola Libros Ediciones.
Beckmann, P. (2007), La Historia de π. México. Editorial Trillas.
Cordero, F. y Suárez. L. Modelación en matemática educativa. (Clame 2005).
Flores, C. y Contreras, B. Geometría dinámica en la clase de matemáticas. (Clame 2005).
Kline, Morris. El pensamiento matemático de la antigüedad a nuestros días. Madrid,
Editorial Alianza. Tomos I , II y III.
Lehmann, Charles. Geometría Analítica. Editorial Limusa. Máxico, 1994.
Pombo, A. (2002), La cuadratura del círculo. Barcelona. Alianza Editorial.
http://xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.html
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Curves.html
http://www.mathcurve.com/courbes2d/courbes2d.shtml
- 11 -