Capitulo IV - Inecuaciones

UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Capitulo IV - Inecuaciones
Definición:
Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que
sólo se verifica para determinados valores de la incógnita o incógnitas.
Ejemplo: La desigualdad: 2x + 1 > x + 5, es una inecuación por que tiene una incógnita “x” que se
verifica para valores mayores que 4.
Intervalos:
Los intervalos son sub-conjuntos de los números reales que sirven para expresar la solución de las
inecuaciones, estos intervalos se representan gráficamente en la recta numérica real.
Consideremos los siguientes tipos de intervalos:
a)
Intervalo Cerrado.- a < b
[ a,b ] = { x ∈ R / a < x < b }
b)
b
a
b
a
b
Intervalo Abierto en a y Cerrado en b.< a,b ] = { x ∈ R / a < x < b }
e)
a
Intervalo Cerrado en a y Abierto en b.[ a,b > = { x ∈ R / a < x < b }
d)
b
Intervalo Abierto.- a < b
< a,b > = { x ∈ R / a < x < b }
c)
a
Intervalos Infinitos.[ a, +∞ > = { x ∈ R / x > a }
< a, +∞ > = { x ∈ R / x > a }
a
a
< -∞, b ] = { x ∈ R / x < b }
< -∞, b> = { x ∈ R / x < b }
< -∞, +∞ ] = { x / x ∈ R }
Nota 1:
Si x ∈ [a,b] ÅÆ a < x < b
Ejemplo.- Demostrar que: si x ∈ [2,4] entonces 2x + 3 ∈ [7,11]
Solución:
x ∈ [2,4] Æ 2 < x < 4, multiplicando por 2
4 < 2x < 8, sumando 3
7 < 2x + 3 < 11
Si 7 < 2x + 3 < 11 Æ 2x + 3 ∈ [7,11]
Por lo tanto, si x ∈ [2,4] Æ 2x + 3 ∈ [7,11]
Nota 2:
Si x ∈ <a,b> ÅÆ a < x < b
Página 68 de 167
b
b
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Ejemplo.- Demostrar que: si 2x-6 ∈ <-4,4> Æ x ∈ <1,5>
Solución:
2x-6 ∈ <-4,4> Æ -4 < 2x – 6 < 4, sumando 6
2 < 2x < 10 dividiendo entre 2
1 < x < 5, entonces x ∈ <1,5>
Por lo tanto, si 2x – 6 ∈ <-4,4> Æ x ∈ <1,5>
Conjunto Solución de una Inecuación:
Se llama conjunto solución de una inecuación a todos los números reales que la verifiquen, es decir, que
dichos números reales dan la desigualdad en el sentido prefijado.
Resolución de una Inecuación:
El resolver una inecuación consiste en hallar un conjunto solución; es decir, encontrar el intervalo donde
están los valores que puede tomar la incógnita para que verifique la inecuación.
Inecuación de Primer Grado en una Incógnita:
Las inecuaciones de primer grado en una incógnita, son de la forma:
ax + b > 0 ó
ax + b < 0, a ≠ 0
Para resolver estas inecuaciones se debe considerar a > 0, es decir , si a > 0, entonces:
x>-
b
a
ó
x
<-
b
a
Su representación gráfica es:
-
b
a
x
x
-
b
a
Luego la solución es dada en la forma:
x ∈ < -b/a , +∞ >
ó
x ∈ < - ∞, -b/a >
Ejemplos: Resolver las siguientes inecuaciones.
1.
3x – 4 < x + 6
Solución:
Las inecuaciones de primer grado en una incógnita, se resuelve, expresando la inecuación en la
forma:
En un solo miembro se pone la incógnita, en el otro miembro los números, es decir:
3x – x < 6 + 4, simplificando se tiene: x < 5. es decir: x ∈ <-∞, 5>
5
La solución es: x ∈ <-∞, 5>
2.
3 (x – 4) + 4x < 7x + 2
Solución:
Poniendo en un solo miembro la incógnita y en el otro miembro los números:
3x – 12 + 4x < 7x + 2 Æ 3x + 4x – 7x < 2 + 12 simplificando 0 < 14
Página 69 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Esta desigualdad obtenida es cierta, entonces la solución de la inecuación dada, es el conjunto de
todos los números reales (x ∈ R).
3.
5x – 4 (x + 5) < x – 24
Solución:
En forma análoga a los ejemplos anteriores en un solo miembro ponemos las incógnitas y en el otro
miembro los números.
5x – 4x – x < -24 + 20 simplificando 0 < -4
Como la desigualdad obtenida no es correcta, entonces no hay ningún valor de x, que verifique que
la inecuación dada. Por lo tanto la solución es el vacío (φ).
4.
2 < 5 – 3x < 11
Solución:
Aplicando la propiedad de transitividad:
a<b<c
2 < 5 – 3x < 11
ÅÆ a < b ∧ b < c
ÅÆ
ÅÆ
ÅÆ
-2
La solución es: x ∈ < -2 , 1 ]
Página 70 de 167
2 < 5 – 3x ∧ 5 – 3x < 11
3x < 5 – 2 ∧ 5 – 1 < 3x
x < 1 ∧ -2 < x
1
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Inecuación de Segundo Grado en una Incógnita:
Las inecuaciones de segundo grado en una incógnita son de la forma:
ax2 + bx + c > 0
ó
ax2 + bx + c < 0 ,
a≠0
Donde a,b,c ∈ R, siendo a ≠ 0, la solución de estas inecuaciones, se obtiene mediante las propiedades de
los números reales ó también por medio de la naturaleza de las raíces del trinomio ax2 + bx + c = 0.
a)
CARÁCTER DE LAS RAÍCES DEL TRINOMIO DE SEGUNDO GRADO
ax2 + bx + c = 0 , con a > 0
(1)
Al analizar el valor número de la ecuación (1) dando valores reales a x se presentan tres casos:
1º Caso: Si ∆ = b2 – 4ac > 0, entonces hay dos valores diferentes r1 < r2 que anulan el trinomio
ax2 + bx + c = 0.
Es decir: a (x – r1) (x – r2) = 0, si se hace variar x a lo largo de la recta real resulta:
i)
Cuando x toma valores menores que r1, los factores (x - r1) y (x – r2) son negativos, luego
el trinomio ax2 + bx + c, tiene el mismo signo del coeficiente de “a”.
ii)
Cuando x toma valores intermedio r1 y r2 ; entonces el factor (x - r1) es positivo y el factor
(x – r2) es negativo, luego el trinomio ax2 + bx + c, tiene signo opuesto del coeficiente de “a”.
iii) Cuando x toma valores mayores que r2 ; entonces los factores (x - r1), (x – r2) son positivos,
luego el trinomio ax2 + bx + c, tiene el mismo signo del coeficiente de “a”.
2º Caso: Si ∆ = b2 – 4ac = 0, entonces hay un solo valor real r1 = r2 = r, que anulan el
trinomio ax2 + bx + c = 0, luego como (x – r)2 es positivo, el signo del trinomio ax2 + bx + c
es el mismo del coeficiente de “a”.
3º Caso: Si ∆ = b2 – 4ac < 0, entonces se tiene dos valores no reales r1 = α - βi que anulan el
trinomio ax2 + bx + c , y para cualquier valor de x, el trinomio: ax2 + bx + c tiene el mismo
signo del coeficiente de “a”.
b)
RESOLUCIÓN DE UNA INECUACIÓN DE SEGUNDO GRADO
Para resolver una inecuación cuadrática de las formas ax2 + bx + c >0 ó ax2 + bx + c < 0, donde
a,b,c ∈ R, a ≠ 0, por medio de la naturaleza
de las raíces primero se resuelve la ecuación ax2 + bx + c = 0, y de acuerdo a la naturaleza de las
raíces se presenta tres casos:
1º Caso: Si la ecuación ax2 + bx + c = 0, tiene dos raíces reales diferentes r1 < r2.
+
r1
+
r2
i)
Si la inecuación es de la forma ax2 + bx + c > 0, con a > 0, la solución es todos los valores de x
que pertenecen al intervalo < -∞, r1 > ∪ < r1, + ∞ >.
ii)
Si la inecuación es de la forma ax2 + bx + c < 0, la solución es todos los valores de x que
pertenecen al intervalo < r1 , r2 >.
Página 71 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
2º Caso: Si la ecuación ax2 + bx + c = 0, tiene una raíz real única r1 = r2 = r.
x
r
x
i)
Si la inecuación es de la forma: ax2 + bx + c > 0, con a > 0. La solución es todos los valores de
x ≠ r, es decir: x ∈ <-∞,r> ∪ <r,+∞>.
CS = x ∈ < -∞, r > U < r, +∞ >
ii)
Si la inecuación es de la forma: ax2 + bx + c < 0, con a > 0. No se verifica para ningún valor
real de x.
3º Caso: Si la ecuación ax2 + bx + c = 0, tiene dos raíces no reales.
i)
Si la inecuación es de la forma: ax2 + bx + c > 0, con a > 0. La solución es todos los valores
reales de x.
ii)
Si la inecuación es de la forma: ax2 + bx + c > 0, con a > 0. No se verifica para ningún valor
real de x.
RESUMIENDO EN EL SIGUIENTE CUADRO
Raíces de la Ecuación
Forma de la Inecuación
Conjunto Solución
2
ax + bx + c = 0
Raíces diferentes
<-∞, r1 > ∪ < r2 ,+∞ >
r 1 < r2
ax2 + bx + c > 0, a > 0
Raíz Real Única r
R – {r}
Raíces no reales
R
Raíces diferentes
< r1 , r2 >
r 1 < r2
2
ax + bx + c < 0, a > 0
Raíz Real Única
φ
Raíces no reales
φ
Ejemplos: Resolver las siguientes inecuaciones:
1.
2x – x – 10 > 0
Solución:
Resolveremos la inecuación usando propiedades de los números reales:
a,b > 0 ÅÆ (a > 0 ∧ b > 0) ó (a < 0 ∧ b < 0)
Página 72 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
2x2 – x – 10 > 0 Æ (x + 2) (2x – 5) > 0
(x+2) (2x–5) > 0 ÅÆ (x+2 > 0 ∧ 2x–5 > 0) ∨ (x+2 < 0 ∧ 2x–5 < 0)
ÅÆ (x > -2 ∧ x > 5/2) ∨ (x < -2 ∧ x < 5/2)
-2
5
2
-2
5
2
La solución es: x ∈ < - ∞, -2 > ∪ < 5/2 , + ∞ >
Otra forma de resolver esta inecuación, es por la naturaleza de sus raíces de la ecuación 2x2 – x
– 10 = 0, de donde r1 = -2, r2 = 5/2, luego r1 < r2 y como 2x2 – x – 10 > 0, de acuerdo al cuadro la
solución es: x ∈ < - ∞, -2 > ∪ < 5/2 , + ∞ >
2.
x2 + 8x – 65 < 0
Solución:
Usando propiedades de los números reales:
a2 < b, b > 0 ÅÆ
-
b < a <
b
Completando cuadrados en x2 + 8x – 65 < 0, se tiene:
x2 + 8x + 16 < 65 + 16 Æ (x + 4) 2 < 81, aplicando la propiedad
(x + 4) 2 < 81 ÅÆ - 81 < x + 4 < 81
ÅÆ -9 < x + 4 < 9 ÅÆ -13 < x < 5
La solución es x ∈ < -13 , 5 >
Ahora resolveremos la inecuación por medio de la naturaleza de las raíces de x2 + 8x – 65 = 0, es
decir: (x + 13) (x - 5) = 0 de donde r1 = -13, r2 = 5 de acuerdo al cuadro es: x ∈ < -13 , 5 >
-13
3.
5
x2 + 20x + 100 > 0
Solución:
Mediante propiedad de los números reales se tiene:
x2 + 20x + 100 > 0
Æ (x + 10) 2 > 0 entonces:
∀ x ∈ R; x ≠ -10, (x+10)2> 0, por lo tanto la solución es: x ∈ R– {-10}
Ahora veremos de acuerdo a la naturaleza de las raíces: x2 + 20x + 100 = 0 entonces r = -10,
multiplicidad 2, y como x2 + 20x + 100 > 0, de acuerdo al cuadro de solución es: x ∈ R– {-10}.
4.
x2
+
3x
5
+
9
100
<
0
Solución:
Aplicando la propiedad de los números reales:
∀ x ∈ R; x2 > 0, luego x2
Pero
x + 3
10
2
Página 73 de 167
>
+
0
3x
5
+
9
100
<
0 Æ
x+ 3
10
2
<0
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Entonces no existe ningún valor real para x que verifique a la inecuación, es decir: φ
Ahora resolvemos mediante la naturaleza de las raíces de la ecuación:
x2
+
3x
5
+
9
100
de donde r = -
=
0
3 de multiplicidad dos
10
pero se tiene que: x2
+
3x
5
+
9
100
<
0
y de acuerdo al cuadro la solución es: φ.
Inecuaciones Polinómicas:
Una inecuación polinómica en un incógnita, es de la forma siguiente:
P(x) = anxn + … + a1x + a0 > 0
a)
ó
P(x) = anxn + … + a1x + a0 < 0
RESOLUCIÓN DE UNA INECUACIÓN POLINÓMICAS
Una inecuación polinómicas de la forma P(x) > 0 ó P(x) < 0, se resuelve de acuerdo a la
naturaleza de sus raíces de la ecuación polinómica P(x) = 0, en una forma sencilla y rápida ,
considerando an > 0.
Para esto hallaremos primero las raíces del polinomio P(x) = anxn + … + a1x + a0 = 0, y como éste
polinomio es de grado n entonces tiene n raíces, lo cual pueden ser reales diferentes, reales de
multiplicidad y no reales.
1º Caso: Cuando las raíces de la ecuación polinómica P(x) = 0, son reales diferentes. Es decir: r1
< r2 < … < rn-1 < rn
+
……
-
+
rn-3
rn-2
rn-1
+
rn
i)
En los intervalos consecutivos determinados por las raíces del polinomio P(x) = 0, se alternan
los signos “+” y “-“ reemplazando por asignar el signo (+) al intervalo < rn , ∞ >.
ii)
Si la inecuación polinómica es de la forma: P(x) = anxn + … + a1x + a0 > 0, an > 0; el
conjunto solución, será la unión de los intervalos a los cuales se le ha asignado el signo “+”.
iii)
Si la inecuación polinómica es de la forma: P(x) = anxn + … + a1x + a0 < 0, an > 0; el
conjunto solución, será la unión de los intervalos a los cuales se le ha asignado el signo “-”.
Ejemplo: Resolver las inecuaciones siguientes:
1.
x5 + 3x4 – 5x3 – 15x2 + 4x + 12 > 0
Solución:
Expresamos el 1º miembro de la inecuación en forma factorizada:
(x + 3) (x + 2) (x – 1) (x + 1) (x – 2) = 0
1
3
-5
-15
4
12
1
4
-1
-16
-12
1
4
-1
-16
-12
0
Página 74 de 167
1
2
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
2
12
22
12
1
6
11
6
0
-1
-5
-6
1
5
6
0
-2
-6
3
0
1
-1
-2
-2
-3
1
0
Luego las raíces son: r1 = -3, r2 = -2, r3 = -1, r4 = 1, r5 = 2
-
+
-3
-
+
-2
-1
1
+
2
Como P(x) > 0, la solución es la unión de los intervalos donde aparecen el signo (+).
Es decir: x ∈ < -3,-2 > ∪ < -1 , 1> ∪ < 2, +∞ >
2.
2x3 – 3x2 – 11x + 6 < 0
Solución:
Hallaremos las raíces de la ecuación: 2x3 – 3x2 – 11x + 6 = 0
2
2
2
-3
-11
6
-4
14
-6
-7
3
0
6
-3
-1
0
-2
3
1/2
1
2
0
Luego las raíces del polinomio son: r1 = -2,
-
+
-2
r2 = ½, r3 = 3
½
+
3
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos donde
aparecen el signo (-), es decir:
x ∈ < - ∞ , -2 > ∪ < ½ , 3 >
2º Caso: Si algunas de las raíces del polinomio P(x) = 0, son reales de multiplicidad de orden
mayor que 1 se tiene:
i)
Cuando el orden de la multiplicidad de una de las raíces del polinomio P(x) = 0 es par, en este
caso a la raíz no se considera para la determinación de los intervalos y para dar la solución se
sigue el mismo proceso del 1º caso.
ii)
Cuando el orden de la multiplicidad de una de las raíces del polinomio P(x) = 0 es impar, en
este caso a la raíz se considera para la determinación de los intervalos y para dar la solución
se sigue el mismo proceso del 1º caso.
Página 75 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Ejemplo: Resolver las inecuaciones siguientes.
1.
(x – 1)2 (x + 2) 8x + 4) > 0
Solución:
Resolviendo la ecuación (x – 1)2 (x + 2) 8x + 4) = 0, de donde r1 = -4, r2 = -2, y r3 = 1, de
multiplicidad 2.
+
-
+
-4
-2
1
Como la inecuación es de la forma P(x) > 0, la solución es la unión de los intervalos donde
aparecen el signo (+), es decir:
x ∈ <-∞,-4> ∪ < -2, +∞ > - {1}
2.
(2x + 1) (3x – 2)3 (2x - 5) < 0
Solución:
Resolviendo la ecuación (2x + 1) (3x – 2)3 (2x - 5) = 0, de donde r1 = - 1/2, r2 = 2/3 de
multiplicidad 3, r3 = 5/2.
-
+
-
- 1/2
2/3
+
5/2
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos donde
aparecen el signo (-). Es decir:
x ∈ <-∞,- 1/2 > ∪ < 2/3, 5/2 >
3º Caso: Cuando alguna de las raíces del polinomio P(x) = 0, no son reales, en este caso a estas
raíces no se consideran en la determinación de los intervalos y para dar la solución se sigue el
mismo procedimiento de los casos anteriores.
Ejemplo: Resolver las inecuaciones siguientes.
1.
(x2 – 7) (x2 + 16) (x2 – 16) (x2 + 1) < 0
Solución:
Resolviendo la ecuación: (x2 – 7) (x2 + 16) (x2 – 16) (x2 + 1) = 0, de donde:
r1 = -4 , r2 = -
+
7, r3 =
7, r4 = 4, r5 = -4i, r6 = 4i , r7 = i, r8 = -i
-4
+
-
7
7
+
4
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos donde
aparecen el signo (-), es decir:
x ∈ < -4,2.
7 > ∪ <
(1 + x + x2) (2 – x – x2) > 0
Solución:
La inecuación la expresamos así:
(x2 + x + 1) (x2 + x – 2) < 0
Página 76 de 167
7, 4 >
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Ahora resolviendo la ecuación: (x2 + x + 1) (x2 + x – 2) = 0, de donde:
r1 = -2,
r2 = 1,
r3 = -1 + 3i,
2
+
r4 = -1 - 3i
2
-2
+
1
Como la inecuación es de la forma P(x) < 0, la solución es la unión de los intervalos donde
aparecen el signo (-), es decir:
x ∈ [-2,1]
Inecuaciones Fraccionarias:
Una inecuación fraccionaria en un incógnita es de la forma:
P(x) > 0
Q(x)
Q(x)
ó
P(x) < 0,
Q(x) ≠ 0
Donde P(x) y Q(x) son monomios o polinomios diferente de cero.
Para resolver una inecuación fraccionaria debe tenerse en cuenta que las inecuaciones:
P(x) >
Q(x)
0
ó
P(x) <
Q(x)
P(x), Q(x) > 0 ó
0, son equivalentes a las inecuaciones:
P(x), Q(x) < 0
Es decir: Si Q(x) ≠ 0 Æ Q2(x) > 0, de donde se tiene:
Si
P(x) >
Q(x)
0
Æ P(x) . Q2 (x) >
Q(x)
0.Q2 (x) Æ P(x). Q(x) > 0
Si
P(x) <
Q(x)
0
Æ P(x) . Q2 (x) <
Q(x)
0.Q2 (x) Æ P(x). Q(x) < 0
Ejemplo: Resolver las inecuaciones siguientes :
1.
(x2 – 1) (x + 3) (x – 2) > 0
(x – 5) (x + 7 )
Solución:
La inecuación (x2 – 1) (x + 3) (x – 2) > 0
(x – 5) (x + 7 )
Es equivalente a la siguiente inecuación:
(x2 – 1) (x + 3) (x – 2) (x - 5) (x + 7) > 0, para x ≠ -7,5
Ahora hallaremos las raíces de la ecuación:
(x2 – 1) (x + 3) (x – 2) (x - 5) (x + 7) = 0.
De donde: r1 = -7, r2 = -3, r3 = -1, r4 = 1, r5 = 2, r6 = 5, que son reales diferentes.
+
-7
+
-3
-1
+
1
2
+
5
Como la inecuación es de la forma P(x) < 0, la solución es la unión de
Q(x)
los intervalos donde aparecen el signo (+), es decir:
x ∈ < - ∞, -7 > ∪ < -3, -1 > ∪ < 1 , 2 > ∪ < 5, +∞ >
Página 77 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
2.
x–2 <
x+3
x+1
x
Solución:
La inecuación dada se expresa en la forma, mayor que cero o menor que cero, es decir: x – 2
x + 1 < 0 -Æ x (x-2) – (x+1) (x+3)
x+3
x
x (x + 3)
de donde:
<
-6x – 3 < 0 Æ 2x + 1 , que es equivalente a:
x (x+3)
x (x+3)
x (2x + 1) (x + 3) x > 0, para x ≠ -3,0
Ahora encontramos las raíces de la ecuación:
(2x + 1) (x + 3) x = 0
De donde: r1 = -3, r2 = - ½ , r3 = 0
-
+
-3
-½
+
0
Como la inecuación es de la forma (2x+1) (x+3) x > 0, la solución es la unión de los intervalos
donde aparecen el signo (+), es decir:
x ∈ < - 3, - ½ > ∪ < 0, +∞ >
3.
x
x–1
+
x–1
x
<
2x
x+1
Solución:
La inecuación dada expresaremos en la forma:
x
+ x–1 2x
< 0
x–1
x
x+1
x2 (x + 1) + (x – 1) (x – 1) (x + 1) – 2x2 (x – 1) < 0, simplificando
(x – 1) x (x + 1)
2x2 – x + 1 < 0,
(x – 1) x (x + 1)
que es equivalente a la inecuación.
(2x2 – x + 1) (x – 1) (x + 1) < 0, para x ≠ -1,0,1
Ahora encontramos las raíces de (2x2 – x + 1) (x – 1) (x + 1) = 0
De donde sus raíces son:
r1 = -1, r2 = 0, r3 = 1, r4 = 1 + √7i, r5 = 1 – √7i
4
4
-
+
-
+
-1
0
1
Como la inecuación es de la forma P(x) < 0, la solución es la unión de
Q(x)
los intervalos donde aparecen el signo (-), es decir:
x ∈ < - ∞, - 1> ∪ < 0, 1 >
Página 78 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Inecuaciones Exponenciales:
Las inecuaciones exponenciales en un incógnita son de la forma:
af(x) > ag(x)
∨
af(x) < ag(x)
Donde f(x) y g(x) son expresiones en x, a ∈ R+ , a ≠ 1.
Para resolver estas inecuaciones, se consideran dos casos:
1º Caso: Si a > 1, entonces los exponentes de la inecuación dada son desiguales en el mismo sentido
prefijado, es decir:
Si af(x) > ag(x) ÅÆ
Si a
f(x)
<a
g(x)
ÅÆ
f(x) > g(x)
f(x) < g(x)
2º Caso: Si 0 < a < 1, entonces los exponentes de la inecuación dada son desiguales en sentido
contrario prefijado, es decir:
Si af(x) > ag(x) ÅÆ
Si a
f(x)
<a
g(x)
ÅÆ
f(x) < g(x)
f(x) > g(x)
Ejemplos: Resolver las siguientes inecuaciones:
1.
3
3
(5x + 1)/3
<
9
3 (x+1)/5
Solución:
La inecuación dada es equivalente a:
3(5x + 1)/9 < 9(3x + 1)/10
Æ
3(5x + 1)/9 < 3(6x + 6)/10
Como a = 3 > 1 entonces 5x + 1 < 6x + 6
9
10
5x + 10 < 54x + 54 Æ -44 < 4x Æ x > -11 Æ x ∈ < -11, + ∞ >
∴ La solución es: x ∈ < -11, + ∞ >
2.
[ (0,2)(x+1)(x-2) ]
1/(x-3)
>
(0.0128)
83x-1
3x-1
Solución:
La inecuación dada se puede escribir en la forma:
(0,2)(x+1) (x-2) / x-3
De donde: (0,2)
>
0.0128
8
(x+1) (x-2) / x-3
3x - 1
> (0,2)12x-4
Como a = 0.2 < 1, se tiene (x+1) (x-2) <
x-3
12 - 4
Æ (x+1) (x-2) - 12 + 4 < 0
x–3
Efectuando operaciones y simplificando tenemos: 11x2 – 39x + 14 > 0,
x-3
esta inecuación es equivalente a: (11x2–39x+14) (x–3) > 0 para x ≠ 3.
Ahora hallando las raíces de: (11x2–39x+14) (x–3) = 0, de donde:
r1 = 39 - 905,
22
r2 = 3,
Página 79 de 167
r3 = 39 + 905
22
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
-
+
-
39 + 905
22
3
+
39 +
905
22
Como la inecuación es de la forma P(x) > 0, la solución es la unión de
Q(x)
los intervalos donde aparece el signo (0), es decir:
x∈
39 -
905 , 3
22
∪
39 +
905, ∞
22
Inecuaciones Irracionales:
Las inecuaciones irracionales en un incógnita son de la forma:
F(x,
F(x,
P2(x),
3
P3(x), ……
n
Pn(x) ) > 0
P2(x),
3
P3(x), ……
n
Pn(x) ) < 0
ó
Donde P2(x), P3(x), ……, Pn(x) son monomios o polinomios diferentes de cero.
Para que la solución de la inecuación sea válida debe resolverse antes la condición Pi(x) > 0, i = 2,3,…, n
en las expresiones con una radical par, cuyo conjunto solución constituirá el universo dentro del cual se
resuelve la inecuación dada. Debe observarse que
P(x), quiere decir, (+ P(x)) y si se desea la raíz
negativa se escribirá expresamente como (- P(x)); es decir:
i) ∀ P(x) > 0 ,
P(x)
> 0
ii)
P(x) = 0 ÅÆ P(x) = 0
Para resolver las inecuaciones radicales se debe tener en cuenta la siguientes propiedades:
1. 0 < x < y
ÅÆ 0 <
x <
y
2. 0 < x < y
ÅÆ 0 <
x <
y
3. 0 < x < y
ÅÆ 0 <
x <
y
4. i) Si n es un entero positivo par.
a1) ∀ P(x) > 0 ∴
n
Pn(x)
> 0 ÅÆ P(x) > 0
a2)
n
P(x) = 0 ÅÆ P(x) = 0
a3)
n
P(x) <
n
Q(x)
ÅÆ
0 < P(x) < Q(x)
ii) Si n es entero positivo impar.
b1)
n
b2)
n
P(x) < 0 ÅÆ P(x) < 0
b3)
n
P(x) <
P(x)
> 0 ÅÆ P(x) > 0
n
Q(x)
ÅÆ
P(x) < Q(x)
Las propiedades b1), b2) indican que
Página 80 de 167
n
P(x)
tienen el mismo signo que P(x) si n es impar.
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
OBSERVACIÓN.- Cuando en una expresión existen k radicales par entonces se calculan los universos
relativos U1, U2, ……, Uk para cada radical y el universo general será U = U1 ∩ U2 ∩ …… ∩ Uk.
Daremos algunos ejemplos de ilustración de estas propiedades, para después estudiar las diversas
formas de inecuaciones irracionales.
Ejemplos: Resolver las siguientes inecuaciones:
1.
x + 5 > -2
Solución:
Como
x + 5 > -2 es válida para todo x tal que x ∈ U: x + 5 > 0 Æ x > -5 Æ U = [-5 , + ∞ >,
luego el conjunto solución es [-5 , + ∞ >
2.
x+7 >0
Solución:
Como
x + 7 > 0 entonces el conjunto universal es x + 7
Además
> 0 Æ U = [-7,+ ∞>.
x + 7 > 0 ÅÆ x + 7 > 0 Æ x ∈ <-7, +∞>.
∴ x ∈ <-7, +∞>.
3.
x–5 < 0
Solución:
Como x – 5 < 0, el conjunto universal es x – 5 > 0 Æ x > 5 Æ U= [5,+∞> y como 0 <
5 < 0 ÅÆ x – 5 = 0 Æ x – 5 = 0 Æ x = 5 ∈ U, luego el conjunto solución es {5}.
4.
x–
x–8 <0
Solución:
Como
5.
x – 8 < 0 es absurdo, entonces la solución es φ.
x+9>0
Solución:
Como
x + 9 > 0 es verdadero ∀ x ∈ U: x + 9 > 0, es decir
solución es x ∈ [-9, +∞>.
6.
8 – 2x <
13
Solución:
El conjunto universal es 8 – 2x > 0 Æ x < 4 de donde U = <-∞, 4].
8 – 2x <
13 ÅÆ 8 – 2x < 13 Æ x > - 5/2
De donde x ∈ [- 5/2, +∞>
Luego el conjunto solución es: U ∩ [- 5/2, +∞> = [- 5/2, 4]
Página 81 de 167
U=[-9, +∞>, luego el conjunto
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
7.
x+3
+
4–x
> -3
Solución:
Calculando los universo relativos.
U1 : x + 3 > 0 Æ x > -3 Æ x ∈ [-3, +∞>
U2 : 4 - x > 0 Æ x < 4 Æ x ∈ [-∞, 4>
U = U1
∩ U2 = [ -3, + ∞ >
∩
<-∞, 4 ] =
[-3, 4]
Como la suma de dos positivos es siempre mayor que un negativo.
x+3 +
8.
4–x
> -3
es válido ∀ x ∈ U = [-3, 4].
x–7 >3
Solución:
Sea U: x – 7 > 0 Î x > 7 Æ x ∈ [7, +∞ >
x – 7 > 3 ÅÆ x – 7 > 9 Æ x > 16 Æ x ∈ <16, +∞ >
El conjunto solución es x ∈ U ∩ < 16, +∞ > = < 16, +∞ >
9.
-
x–5
>0
Solución:
-
x–5
> 0 ÅÆ
x2 – x – 12
10.
-
x–5
< 0 el conjunto solución es φ.
x2 – 6x + 5
<
Solución:
Calculando los universo relativos.
U1 : x2 – x - 12 > 0 Æ (x – 4) (x + 3) > 0
U1 = < -∞ , -3 ] ∪ [ 4, +∞ >
+
-
+
-3
4
U2 : x2 – 6x + 5 > 0 Æ (x – 5) (x - 1) > 0
U12 = < -∞ , 1 ] ∪ [ 5, + ∞ >
+
-
+
1
U = U1
∩ U2 = < - ∞, -3 ]
x2 – x – 12
5
∪
[ 5, +∞ >
x2 – 6x + 5
<
ÅÆ x2 – x – 12 < x2 – 6x + 5
de donde 5x < 17 Æ x < 17/5 Æ x ∈ < -∞ , 17/5 ]
Luego el conjunto solución es: x ∈ U ∧ < -∞ , 17/5 ] = <-∞ , 17/5 ]
11.
3
x2 – 4 (x – 2)2 (x3 – 13x + 12)
3
3
2
(x + 4) (x + 8x + 4x - 48)
Página 82 de 167
>
0
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Solución:
Como 3 x2 - 4 tiene el mismo signo que x2 – 4 y (x + 4) 3 tiene el mismo signo que x + 4 entonces
la inecuación dada es equivalente.
3
x2 – 4 (x – 2)2 (x3 – 13x + 12)
>
0
ÅÆ
(x + 4)3 (x3 + 8x2 + 4x - 48)
(x2 – 4) (x -2)2 (x3 – 13x + 12)
(x + 4) (x3 + 8x2 + 4x - 48)
>
0
Como ∀ x ∈ R, (x - 2)2 > 0 entonces:
(x2–4) (x -2)2 (x3 – 13x + 12)
(x + 4) (x3 + 8x2 + 4x - 48)
>
(x + 2) (x - 2) (x – 1) (x2 + x - 12)
(x + 4) (x – 2) (x + 6) (x + 4)
(x + 2) (x - 1) (x + 4) (x - 3)
(x + 6)
-
+
-6
>
(x2 – 4) (x3 – 13x + 12)
(x+4) (x3+8x2+4x-48)
0 ÅÆ
>
0 , para x ≠ 2, -4
0 , para x ≠ 2, -4
-
+
-4
-
-2
+
1
3
Luego el conjunto solución es:
x ∈ < -6 , -4 ] ∪ [ -2, 1 ]
12.
3
∪ [ 3 , +∞ >
5
x + 7 (x – 2)4 (x + 3)3
x2 – 7x + 12
4
6
x + 9 (x – 8)3 (x3 - 27) (x2 – 14x + 48)
10 - x
<
0
Solución:
Los radicales pares nos da el universo U.
10 – x > 0 ∧ x + 9 > 0 Æ x < 10 ∧ x>-9 Æ x ∈ <-9, 10]
Æ U = <-9 , 10 ]
(no se incluye el -9 por que anula al denominador).
Como los radicales pares son positivos la inecuación es equivalente a:
5
x + 7 (x – 2)4 (x + 3)3
3
6
x + 9 (x – 8)3 (x3 - 27) (x2 – 14x + 48)
5
x + 7 (x – 2)4 (x + 3)3
3
x2 – 7x + 12
4
x2 – 7x + 12
10 - x
<
<
0
ÅÆ
0
(x – 8)3 (x3 - 27) (x2 – 14x + 48)
Como los radicales impares tienen el mismo signo que las cantidades subradicales entonces:
(x + 7) (x – 2)4 (x + 3) (x2 – 7x + 12)
(x – 8)3 (x - 3) (x2 – 3x + 9) (x – 6) (x – 8)
<
0
Como para todo x ∈ R (x + 2)4 > 0
(x + 7) (x + 3) (x - 3) (x – 4)
(x – 8)3 (x - 3) (x – 6) (x – 8)
Página 83 de 167
<
0, para x ≠ 3, 8
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Simplificando tenemos:
(x + 7) (x + 3) (x – 4)
x-6
+
<
-7
0, x ≠ 3, 8
+
-
-3
4
+
6
x ∈ [ -7, -3 ] ∪ [ 4, 6 > luego el conjunto solución es: x ∈ U ∩
( [ -7, -3 ] U [ 4, 6 >)
∴ x ∈ [ -7, -3 ] U [ 4, 6 >
Ahora veremos como resolver diversas formas de la inecuación con radicales aplicando criterios de
acuerdo a cada tipo de inecuación irracional.
1.
Para las inecuaciones irracionales de las formas:
a)
P(x) > Q(x). La solución se obtiene así:
P(x) > Q(x) ÅÆ ( P(x) > 0 ∧
b)
P(x) > Q(x). La solución se obtiene así:
P(x) > Q(x) ÅÆ ( P(x) > 0 ∧
2.
[ Q(x) < 0 ∨ (P(x) > 0 ∧ P(x) > Q2(x))])
Para las inecuaciones irracionales de las formas:
a)
P(x) < Q(x). La solución se obtiene así:
P(x) < Q(x) ÅÆ ( P(x) > 0 ∧
b)
[ Q(x) < 0 ∨ (P(x) > 0 ∧ P(x) < Q2(x))])
P(x) < Q(x). La solución se obtiene así:
P(x) < Q(x) ÅÆ ( P(x) > 0 ∧
3.
[ Q(x) < 0 ∨ (P(x) > 0 ∧ P(x) > Q2(x))])
[ Q(x) < 0 ∨ (P(x) > 0 ∧ P(x) < Q2(x))])
Para las inecuaciones irracionales de las formas:
a)
P(x) +
Q(x) > 0. La solución se obtiene así:
P(x) + Q(x) > 0 Æ P(x) > 0 ∧
b)
P(x) +
Q(x) > 0. La solución se obtiene así:
P(x) + Q(x) > 0 Æ P(x) > 0 ∧
4.
Q(x) > 0
Q(x) > 0
Para la inecuación irracional de la forma:
P(x) +
Q(x) > K, K > 0. La solución se obtiene así:
P(x) + Q(x) > K Æ [ (P(x) > 0 ∧ Q(x) > 0 ) ∧ (P(x) > (k –
5.
Para las inecuaciones irracionales de la forma:
P(x) +
Q(x) < 0 . La solución se obtiene así:
P(x) +
Q(x) < 0 Æ P(x) = 0 ∧ Q(x) = 0
Página 84 de 167
Q(x))2 ]
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
OBSERVACIÓN.Consideremos otros casos más generales.
1º Caso: Si n es impar positivo mayor que uno.
a)
n
P(x)
Q(x) > 0
P(x). Q(x)
ÅÆ
R(x)
b)
c)
R(x)
P(x)
R(x)
n
n
< 0
P(x)
ÅÆ
Q(x)
P(x) <
> 0
n
> 0
R(x) Q(x)
Q(x) ÅÆ P(x) < Q(x)
2º Caso: Si n es par positivo.
a)
n
P(x) Q(x) > 0
ÅÆ
P(x) > 0 ∧ Q(x)
> 0
b)
n
P(x) Q(x) < 0
ÅÆ
P(x) > 0 ∧ Q(x)
< 0
c)
P(x)
ÅÆ
Q(x) > 0 ∧ P(x)
> 0
Q(x) R(x)
n
Q(x) R(x)
n
P(x) > Q(x) ÅÆ ( P(x) > 0 ∧ [ Q(x) < 0 ∨ ( P(x) > 0 ∧ Q(x) > 0 ∧
d)
e)
<0
n
R(x)
P(x)
<0
Q(x) > 0 ∧ P(x)
ÅÆ
< 0
R(x)
P(x) > Qn (x)) ]
f)
n
P(x) < Q(x) ÅÆ P(x) > 0 ∧ [(Q(x) < 0) ∧ P(x) < Qn(x)]
Ejemplo: Resolver la siguientes inecuaciones.
1.
x2 – 14x + 13
>
x–3
Solución:
x2 – 14x + 13
ÅÆ
ÅÆ
ÅÆ
ÅÆ
ÅÆ
ÅÆ
>
x – 3 ÅÆ x2 – 14x + 13 > 0 ∧ [x - 3 < 0 ∨
( x2 – 14x + 13 > 0 ∧ x2 – 14x + 13 > (x-3)2)]
x2 – 14x + 13 > 0 ∧ [x < 3 ∨ ( x2 – 14x + 13 > 0 ∧ x < ½)]
x2 – 14x + 13 > 0 ∧ [x < 3 ∨ x ∈ <-∞, 1] ∪ [13, ∞> ∧ x < ½]
x2 – 14x + 13 > 0 ∧ [x < 3 ∨ x < ½)]
x2 – 14x + 13 > 0 ∧ x < 3
(x – 13) (x – 1) > 0 ∧ x < 3
x ∈ <-∞, 1] ∪ [13, ∞> ∧ x < 3
∴ x ∈ <-∞, 1]
2.
x2 – 14x + 13
<x+1
Solución:
Aplicando la parte b) del 1º caso:
x2 – 14x + 13
ÅÆ
ÅÆ
ÅÆ
ÅÆ
3.
< x + 1 ÅÆ (x2 – 14x + 13 > 0 ∧ [ x+1 > 0) ∧
(x2 – 14x + 13 < ( x+1)2 ])
((x – 13) (x- 1) > 0 ∧ [ x > -1) ∧ ((x – 13) (x – 1) < (x + 1)2 ])
((x – 13) (x- 1) > 0 ∧ [ x > -1) ∧ x > ¾]
x ∈ <-1,1] ∪ [13, +∞> ∧ x > ¾
x ∈ < ¾ , 1] ∪ [13, +∞>
2x – 8
x–1
+
5–x
x+3
Página 85 de 167
>
0
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Solución:
Aplicando la parte b) del 3º caso:
P(x) +
2x – 8
x–1
Q(x) > 0 ÅÆ P(x) > 0 ∧ Q(x) > 0
+
5 – x ÅÆ 2x – 8 > 0 ∧ 5 – x > 0
x+3
x–1
x+3
ÅÆ (x – 4) (x – 1) > 0, x ≠ 1 ∧ (5 – x) (x +3) > 0, x ≠ 3
ÅÆ (x – 4) (x – 1) > 0, x ≠ 1 ∧ (x - 5) (x +3) > 0, x ≠ -3
+
-
+
1
4
+
-
+
-3
5
x ∈ < - ∞, 1 > ∧ x ∈ < - 3, 5 >
-3
1
4
5
La solución es : x ∈ < - 3, 5 > ∪ [ 4, 5 ]
Valor Absoluto
Al valor absoluto del número real x denotaremos por |x|, y se define por la regla.
x si x > 0
|x| =
-x si x < 0
Ejemplo: |7| = 7,
|-7| = - (-7) = 7
Propiedades del Valor Absoluto:
1.|a| > 0, ∀ a ∈ R
3.|a| =|-a|
2.|a| > a ∀ a ∈ R
4.|ab|=|a||b|
5. a =|a| , b ≠ 0
b
|b|
6.|a+b|<|a|+|b|
(desigualdad triangular)
Demostraremos la 6º propiedad, las demás dejamos para el lector.
|a+b|=|(a+b)2|=(a+b)2=a2+2ab–b2< |a|2+2|a||b|+|b|2=(|a|+|b|)2
|a + b|2 =
(|a| + |b|)2 entonces:
Página 86 de 167
∴ |a + b| <
|a| |b|
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Propiedades Básicas para resolver ecuaciones e inecuaciones donde interviene Valor Absoluto:
1.
2.
3.
4.
5.
6.
|a| = 0 ÅÆ a = 0
|a| = b ÅÆ [ b > 0 ∧ (a = b ∨ a = -b) ]
|a| = |b| ÅÆ a = b ∨ a = -b
Si b > 0, entonces:
i) |a| < b ÅÆ -b < a < b
ii) |a| < b ÅÆ -b < a < b
Si a,b ∈ R se verifica:
i) |a| > b ÅÆ b > a > -b
ii) |a| > b ÅÆ a > b ∨ a < -b
i) |a| =
a2
ii) |a|2 =
a2
Ejemplos:
1.
Resolver la ecuación |4x + 3| = |7|
Solución:
|4x+3|=|7| ÅÆ4x+3=7 ∨ 4x+3=-7 ÅÆ x=1 ∨ x =- 5/2
Luego para x = 1, x = - 5/2 son soluciones para la ecuación dada.
2.
Resolver la ecuación |2x + 2| = 6x - 18
Solución:
|2x+2|=6x–18ÅÆ[6x–18>0∧(2x+2)=6x-18 ∨
2x+2=-6x+18)]
ÅÆ [ x > 3 ∧ (x = 5 ∨ x = 2) ]
2
3
5
Luego la solución de la ecuación es x = 5.
3.
Resolver la ecuación |x - 2| = |3 – 2x|
Solución:
|x - 2| = |3 – 2x| ÅÆ x – 2 = 3 – 2x ∨ x – 2 = -3 + 2x
ÅÆ x = 5/3 ∨ x = 1, la solución es:
4.
{1,5/3}
Hallar el valor de la expresión |4x+1|-|x–1|,si x∈ <0,1>
x
Solución:
4x + 1, x > - ¼
|4x + 1|=
x – 1 , x > 1
,
|x-1| =
-4x – 1, x < - ¼
1 – x , x < 1
Si x ∈ <0,1> Æ |4x + 1| = 4x + 1, |x - 1| = 1 – x
Luego:
|4x+1|-|x-1|
x
=
4x+1–(1- x)
x
∴ |4x + 1| - |x - 1|
x
=
5
Página 87 de 167
=
5x
x
= 5
, para x ∈ <0,1>
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
5.
Resolver la inecuación
2x – 5
x – 6
< 3
Solución:
2x-5 <3 ÅÆ - 3<2x–5 <3 ÅÆ-3<2x–5
x-6
x-6
x-6
ÅÆ 5x – 23
x – 6
> 0
∧
∧
2x – 5 < 3
x-6
x – 13 > 0
x- 6
ÅÆ (5x – 23) (x – 6) > 0 ∧ (x – 13) (x – 6) > 0, x ≠ 6
+
-
+
23/5
+
6
6
13
x ∈ < -∞, 23/5 > ∪ < 6, +∞> ∧ < -∞, 6 > ∪ < 13, +∞>
23/5
6
13
La solución es: x ∈ < -∞, 23/5 > ∪ < 13, +∞>
M áx imo E nt e r o
Si x es un número real, el máximo entero de x representaremos por [ |x| ] y es el
mayor de todos los enteros menores o iguales a x, es decir:
[ |x| ] = máx { n ∈ Z / x > n }
Para calcular el máximo entero de un número real x, se observa todos los enteros
que sea encuentran a la izquierda de x (o que coinciden con x, en caso que x sea
entero) y el mayor de todos ellos es el máximo entero [|x|], por ejemplo:
-1
0
1
2
x
3
4
5
3
3.7 4
5
De donde: [ |x| ] = 2
Ejemplo: Hallar [|3,7|]
-1
0
1
2
De donde [|3,7|] = 3
Si x se encuentra entre dos enteros consecutivos de la forma:
n
x
n+1
Entonces:
[|x|] = n ÅÆ n < x
< n + 1, n ∈ Z
Ejemplo: Si [|x|] = 5 ÅÆ 5 < x < 6
[|x|] = -5 ÅÆ -5 < x < -4
Página 88 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Propiedades del Máximo Entero:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
[|x|] ∈ Z
[|x|] = x ÅÆ x ∈ Z
[|x|] < x < [|x|] + 1, ∀ x ∈ R
0 < x - [|x|] < 1, ∀ x ∈ R
[|[|x|]|] = [|x|]
[|x + n|] = [|x|] + n, n ∈ Z
[|x|] < n ÅÆ x < n + 1, n ∈ Z
[|x|] < n ÅÆ x < n, n ∈ Z
[|x|] > n ÅÆ x > n, n ∈ Z
Si y ∈ Z, [|x|] > y ÅÆ x > y
Si y ∈ Z, [|x|] < y ÅÆ x < y + 1
∀ x,y ∈ R, si x < y ÅÆ [|x|] < [|y|]
- [|x + 1|]; x ∈ R - Z
13. [|x|] =
- [|x|] = -x; x ∈ Z
Ejemplos:
1.
Resolver la ecuación
x + 2
x + 3
=
2
Solución:
Se conoce que [|x|] + n ÅÆ n < x
x + 2
x + 3
=2ÅÆ 2 <
x + 2 < 3
x + 3
< n + 1
ÅÆ 2 < 1 -
ÅÆ 1 < - 1 <2ÅÆ1< - 1
x + 3
x + 3
ÅÆ 1 +
ÅÆ
1
< 0
x + 3
x + 4
x + 3
< 0
∧
∧
∧
- 1
x + 3
1
< 3
x + 3
- 1
< 2
x + 3
> 0
2x + 7
x + 3
> 0
ÅÆ[(x+4)(x+3)<0∧(2x+7)(x+3)>0], x≠-3
ÅÆ x ∈ [-4,-3> ∧
x ∈ <-∞, -7/2> ∪ <-3, +∞>
Luego la solución es: x ∈ [ -4 , - 7/2 >
2.
Resolver la inecuación
|x| - 1
5
> 4
Solución:
Aplicando la propiedad siguiente: Si y ∈ Z, [|x|] > y ÅÆ x > y
4 ∈ Z,
|x| - 1
5
> 4ÅÆ |x| - 1 > 4 ÅÆ |x| - 1 > 20
5
ÅÆ |x| > 21 ÅÆ x > 21 ∨ x < -21
La solución es: x ∈ <+-∞,-21] ∪ [21, +∞>
Página 89 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
3.
Resolver la inecuación [||x|-2x|] = 0
Solución:
Por definición de máximo entero se tiene:
[||x|-2x|]=0ÅÆ0<|x|-2x<1 ÅÆ 2x < |x| < 1 + 2x
ahora por la propiedad transitiva: (a<b<cÅÆa<b∧b < c)
se tiene: 2x<|x|<1+2x ÅÆ
2x < |x| ∧
|x| < 1 + 2x
x,x > 0
además se conoce que: |x| =
-x,x < 0
1º Si x > 0 Æ |x| = x reemplazando en (1) se tiene:
2x < 0 ∧ x < 1 + 2x Æ x < 0 ∧ x > -1 Æ x ∈ <-1,0]
La primera parte de la solución es:x∈[0,∞>∧<-1,0]
Æ x = 0
2º x < 0 Æ |x| = -x reempleando en (1) se tiene:
2x<-x∧-x<1+2x Æ x < 0 ∧ x > - 1/3 Æ x ∈ < -1/3, 0]
La segunda parte de la solución es: x∈<-1/3,0]
Æ x ∈ < -1/3,0]
Por lo tanto la solución de: [||x|-2x|] = 0 es:
x ∈ < -1/3,0> ∪ {0} = < -1/3,0]
I ne cua c io n e s L og a r í tmi ca s
Para el estudio de las inecuaciones logarítmicas es necesario recordar lo siguiente:
En primer lugar la definición de logaritmo es decir:
logbN=xÅÆN=bx
En
a)
b)
c)
d)
e)
f)
g)
segundo lugar las propiedades del logaritmo:
logb AB = logbA + logbB
logb A/B = logbA - logbB
logb An = nlogbA
n
logb
A = 1/n logbA
logb 1 = 0
logb b = 1
loga N = logbN
logba
En tercer lugar se observa la gráfica y = logbx cuando b > 1 y 0 < b < 1. También
dentro del campo de los números reales, solo tiene logaritmo los números reales
positivos: ahora graficamos la ecuación y = logbx.
Y
y = logbx
y = logbx
b > 1
0 < b < 1
x1
0
1
x1
x2
X
0
x2
1
Al observar la gráfica se tienen los siguientes casos:
Página 90 de 167
X
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
1º Caso: Cuando la base es b > 1, en
i) Los números mayores que 1 tienen
ii) Los números entre 0 y 1 tienen
x1,x2 ∈R+ se tiene: si b > 1 y 0 <
De
a)
b)
2º
i)
donde
Si x >
Si x >
Caso:
la gráfica podemos observar:
logaritmo positivo.
logaritmo negativo, entonces para cualquier
x1 < x2 ÅÆ logbx1 < logbx2
deducimos las relaciones siguientes:
0, b > 1; N ∈ R Æ logbx > N ÅÆ x > bn
0, b > 1; N ∈ R Æ logbx < N ÅÆ x < bn
Cuando la base es 0 < b < 1, en la gráfica podemos observar:
Los números mayores que 1 tienen logaritmo negativo.
Los números entre 0 y 1 tienen logaritmo positivo, entonces para cualquier
x1,x2 de R+ se tiene:
si 0 > b < 1 y 0 < x1 < x2 ÅÆ logbx1 > logbx2
De donde deducimos las relaciones siguientes:
a) Si x < 0, 0 < b < 1 y
b) Si x > 0, 0 < b < 1 y
N ∈ R Æ logbx > N ÅÆ 0 < x < bN
E ∈ R Æ logbx < N ÅÆ x > bN
Ejemplo: Resolver la inecuación log1/3 (2x + 5) < -2
Solución:
Aplicando la propiedad siguiente: x > 0, 0 < b < 1, N ∈ R, logbx < N
ÅÆ
x > bN
Para nuestro caso 2x + 5 > 0 Æ x > -5/2, tomando logaritmo
log1/3 (2x + 5) < - 2 ÅÆ 2x + 5 > (1/3) -2
2x + 5 > 9 ÅÆ 2x > 4 Æ x > 2, la solución es: x ∈ <2+∞>
Ejemplo: Resolver la inecuación log2 (|x – 2| - 1) > 1
Solución:
Aplicando la propiedad siguiente: x > 0, b > 1, N ∈ R, logbx > N
Para nuestro caso se tiene: |x – 2| - 1 > 0
|x – 2| > 1 ÅÆ x – 2 > 1 ∨ x – 2 < -1 ÅÆ x > 3 ∨ x < 1
log2 (|x – 2| - 1) > 1 ÅÆ |x – 2| - 1 > 2
|x – 2| > 3 ÅÆ x – 2 > 3 ∨ x – 2 < -3 ÅÆ x > 5 ∨ x < -1
La solución es: x ∈ <-∞,-1> ∪ <5, +∞>
Página 91 de 167
ÅÆ
x > bN
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Ejercicios Resueltos
1.
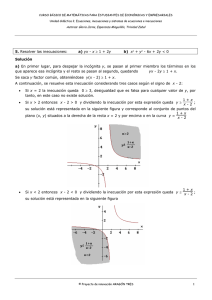
Resolver: 2x2 – 6x + 3 < 0
Solución:
Aplicando la fórmula de la ecuación de segundo grado.
Recordemos: Si: ax2 + bx + c = 0
Entonces: x = -b ±
b2 – 4ac
2a
Luego, la desigualdad: 2x2 – 6x + 3 < 0
Se escribe como una ecuación: 2x2 – 6x + 3 = 0
De donde identificamos: a = 2, b = -6, c = 3
(-6)2 – 4(2)(3)
2(2)
Aplicando la fórmula: x = 6 ±
x = 6 ±
36 - 24
4
x = 6 ± 12
4
x = 6 ±
(4) (3)
4
= 3±
2
3
Llevando los valores de x a la recta de los números reales.
Graficando:
+
-
-∞
3- 3
2
+
3+ 3
2
+∞
Como la desigualdad es menor que cero, el intervalo solución son los negativos.
Por lo tanto:
x
∈
32
2.
3 ;3+ 3
2
Resolver: 1 – x – 2x2 > 0
Solución:
Como el término de mayor grado (-2x2) tiene coeficiente negativo, entonces multiplicamos por (-1)
la inecuación.
Se recomienda al estudiante emplear el método de la fórmula de la ecuación de segundo grado, el
cual es el mejor:
Así: 1 – x – 2x2 > 0
Multiplicando por (-1): 2x2 + x – 1 < 0
Fórmula de la ecuación de segundo grado:
2x2 + x – 1 < 0
Página 92 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
2x2 + x – 1 = 0
Como ecuación:
Identificando: a = 2; b = 1; c = -1
(1)2 – 4(2)(1)
2(2)
Aplicando la fórmula: x = -1 ±
x = -1 ±
1–8
4
x = -1 ± 9
4
De donde:
x1 = - 1 – 3 = -1
4
∧
= -1 ± 3
4
x2 = -1 + 3
4
= 1
2
Graficando y ubicando los valores en la recta:
+
-
-∞
+
-1
1
+∞
2
Como la desigualdad es menor o igual a cero, entonces el conjunto solución es el intervalo negativo:
∈
3.
-1 ,
1
2
Resolver: 4x2 + 9x – 9 < 0
Solución:
4x2 + 9x – 9 < 0
4x2 + 9x –9 = 0
Como la ecuación:
Factorizando por aspa: (4x – 3) (x + 3) = 0
Igualando a cero cada factor:
4x – 3 = 0 Æ x
=
3
4
x + 3 = 0 Æ x = -3
Ubicando estos valores en la recta de los reales.
Graficando: x = 3
4
∧ x = -3
+
-
-∞
Luego:
4.
-1
x ∈
+
3
4
+∞
- 3; 3
4
Resolver: 3 (x + 1) 2 < (x + 4) 2 - 12
Solución:
Desarrollando la expresión:
Página 93 de 167
3 (x + 1) 2 < (x + 4) 2 - 12
3 (x2 + 2x + 1) < x2 + 8x + 16 - 12
3x2 + 6x + 3 < x2 + 8x + 4
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Transponiendo: 3x2 + 6x - x2 - 8x – 4
Reduciendo: 2x2 - 2x2 – 1 <
<
0
0
Como ecuación: 2x2 - 2x2 – 1 = 0, de donde a = 2, b = -2, c = -1
Por fórmula:
x = 2 ±
(-2)2– 4(2)(-1)
2(2)
= 2±2
12
4
4
x2 = 1 – 3
2
x = 2 ±
De donde: x1 = 1 + 3
2
∧
3
Ubicando x1 ∧ x2 en la recta:
+
-
-∞
De donde:
1- 3
2
x ∈
1–
2
5.
+
1+ 3
2
+∞
3 ; 1+ 3
2
Resolver: x2 + 40x + 400 > 0
Solución:
x2 + 40x + 400 > 0
Como ecuación:
x2 + 40x + 400 = 0
(x + 20)2 = 0
Factorizando por aspa:
Extrayendo raíz:
x + 20 = 0
De donde:
x = -20
Ubicando en la recta:
P
+
-∞
+
20
+∞
Cuando el grado del factor es 2, entonces se repite el signo del intervalo.
Luego: x ∈ R – {20}
Página 94 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
6.
x5 + 3x4 – 5x3 – 15x2 + 4x + 12 < 0
Solución:
Aplicando la regla de Ruffini:
1
1
1
-1
1
-2
1
2
1
3
3
-5
-15
4
12
1
4
-1
-16
-12
4
-1
-16
-12
-
-1
-3
4
12
3
-4
-12
-
-2
-2
12
1
-6
-
2
6
3
-
-3
1
-
Æ (x – 1) (x + 1) (x - 2) (x + 3) < 0
-∞
+
-3
-2
+
-1
1
2
x ∈ < -∞; -3 > ∪ < -2 ; -1 > ∪ < 1; 2 >
7.
(2x - 7) (x2 - 9) (2x + 5) > 91
Solución:
(2x - 7) (x2 - 9) (2x + 5) - 91 >
(2x - 7) (x - 3) (x + 3) (2x + 5) - 91 >
[ (2x - 7) (x + 3) ] [ (2x + 5) (x - 3) ] - 91 >
(2x2 – x + 21) (2x2 – x - 15) – 91 >
0
0
0
0
α = 2x2 – x ……… (1)
∴ (α - 21) (α - 15) – 91 > 0
α2 – 36α + 315 – 91 > 0
α2 – 36α + 224 > 0
(α – 28) (α - 8 ) > 0
Para encontrar los valores de (α):
α - 28 = 0 Æ α = 28
α- 8=0Æ α= 8
En (1):
28 = 2x2 – x Æ 2x2 – x – 28 = 0
x=4
x=-
8 = 2x2 – x Æ 2x2 – x – 8 = 0
7
2
x= 1-
65
4
x = 1 + 65
4
Página 95 de 167
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Llevando a la recta los valores de x:
+
-∞
∴x∈
8.
-7
2
-∞; - 7
2
+
1 - 65
4
∪
1 + 65
4
1 - 65 ; 1 + 65
4
4
+
4
∪
+∞
< 4; ∞ >
12x5 – 35x4 – 53x3 + 53x2 + 35x – 12 < 0
Solución:
Aplicando Ruffini:
12
1
12
-35
-53
53
35
-12
12
-23
-76
-23
12
-23
-76
-23
12
-
∴ 12x5–35x4–53x3+53x2+35x–12 = (x-1) (12x4–23x3–76x2–23x+12)
∴ Trabajando con: 12x4 – 23x3 – 76x2 – 23x + 12
Entre x2:
12x2 – 23x – 76 – 23 + 12 = 0
x
x2
12
x2 + 1
x2
– 23
x+1
x
– 76 = 0
α = x + 1 Æ x2 + 1 = α 2 - 2
x
x2
Æ 12 (α2 - 2) - 23α - 76 = 0
12α2 - 23α - 100 = 0
(12α + 25) (α - 4) = 0
∴ 12 α = -25 Æ α = - 25
12
α-4=0Æα=4
α = x + 1 Æ - 25 = x + 1 Æ - 25 = x2 + 1
x
12
x
12
x
- 25x = 12x2 + 12
12x2 + 25x + 12 = 0
(4x + 3) (3x + 4) = 0
x=- 3 , x=- 4
4
3
α=x+ 1 Æ
x
4 = x + 1 Æ 4 = x2 + 1
x
x
4x = x2 + 1 Æ x2 – 4x + 1 = 0
x = 2 + 3, x = 2 - 3
Llevando todos los valores de x a la recta:
-
Página 96 de 167
+
-
+
-
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
-∞
∴x∈
9.
-4
3
-∞; - 4
3
∪
- 3
4
2- 3
- 3 ;2- 3
4
∪
1
2+
1 ;2+ 3
x6 + 15x5 + 78x4 + 155x3 + 78x2 + 15x + 1 < 0
Solución:
Entre x3:
x3 +
x2 + 1
x2
1 + 15
x3
+ 78
x + 1 + 155 = 0 …… (I)
x
Haciendo:
α = x + 1 …… (1)
x
Æ
α2 = x2 + 2 + 1
x2
Æ
α 2 – 2 = x2 + 1
x2
α3 =
x+ 1
x
α3 =
x3 +
1 + 3x2 1 + 3 1 x
x
x2
x3
α3 =
x3 +
1 + 3x + 3
x
x3
α3 =
x3 +
1 +3
x3
…… (2)
3
x+ 1
x
α
α3 =
x3 +
1 + 3α
x3
α3 - 3α = x3 +
1 …… (3)
x3
(1), (2) y (3) en (I):
∴ α3 - 3α + 15α2 – 80 + 78α + 155 = 0
(α + 5)3 = 0 Æ
α=x+1
x
α+5=0
Æ
α = -5
Æ -5 = x + 1
x
Æ x2 + 5x + 1 = 0
∴x = -5±
21
2
Llevando a la recta los valores de x:
+
-∞
-5 - 21
2
∴ x∈
Página 97 de 167
-5-
+
-5 + 21
2
21 ; -5+ 21
+∞
3
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
2
2
10. Resolver: 72x5 – 132x4 + 2x3 + 57x2 – 5x – 6 < 0
Solución:
Para factorizar por Ruffini, cuando el coeficiente del primer término (a0) es diferente, se procede de
la siguiente manera:
1)
Hallar las posibles raíces racionales:
a.
Hallar los divisores de a0 = 72
div (72): + 1, + 2, + 3, + 4, + 6, + 8, + 9, + 12, + 18,
+ 24, + 36, + 72
b.
Hallar los divisores del término independiente (an):
div (6): + 1, + 2, + 3, + 6
Las posibles raíces reales se obtienen dividiendo a cada divisor de a0 entre
(término independiente).
+1, + 1, + 1, + 1, + 2, + 2, + 3, + 3, + 4, + 4, + 6, + 8, + 8,
2
3
6
3
2
3
3
+ 9, + 9, + 12, + 18, + 24, + 36, + 72
2
2)
Factorizando por Ruffini:
72
-132
2
57
-5
6
108
-36
-51
9
6
72
-24
-34
6
4
0
36
-12
-17
3
2
24
8
-6
-2
36
12
-9
-3
0
12
4
-3
-1
6
5
1
10
2
0
3
2
2
3
1
2
12
6
-1
5
1
-2
-1
3
-1
6
3
2
1
2
0
2
Página 98 de 167
0
Sacando mitad a
cada uno de los
términos
Sacando tercia a
cada uno de los
términos
Sacando mitad a
cada uno de los
términos
Sacando tercia a
cada uno de los
términos
los divisores an
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
3)
Escribiendo como producto de factores:
x–3 x - 2 x–1 x+1 x+1
2
3
2
3
2
Puntos críticos:
-∞
C.S.:
x∈
3, 2 , 1, - 1 , - 1
2 3
2
3
2
+
-1/2
-∞ ; 1
2
11. Resolver:
-
+
-1/3
∪
< 0
-
1/2
-1 ; 1
3 2
∪
+
2/3
3/2
+∞
2 ; 3
3
2
1
–
1 <
x2 + x
x2 – x
-1_
x2 - 1
Solución:
1
x2 + x
–
1 <
-1_
x2 – x
x2 - 1
Transponiendo:
1
x2 + x
Factorizando denominadores:
–
1 +
-1_
x2 – x
x2 - 1
<0
1
–
1 +
-1
_<0
x (x+1)
x (x-1) (x+1) (x-1)
m.c.m.: x (x + 1) (x – 1)
Luego:
(x - 1) - (x + 1) + x < 0
x (x + 1) (x – 1)
Simplificando:
x–2
<
x (x + 1) (x – 1)
0
Igualando a cero numerador y denominador:
x–2=0Æx=2
x=0Æx=0
x + 1 = 0 Æ x = -1
x-1=0 Æx=1
Llevando a la recta cada uno de estos valores:
+
-∞
-1
+
0
1
+
2
+∞
De donde: x ∈ < -1 ; 0 > ∪ < 1; 2 >
12. Resolver:
x–3
x+4
>
x-2
x+2
Solución:
x–3
x+4
>
x-2
x+2
Todo al primer miembro:
x–3
x+4
-
x–2 >0
x+2
m.c.m.: (x + 4) (x + 2)
Luego:
(x – 3) (x + 2) – (x - 2) (x + 4) > 0
(x + 4) (x + 2)
Efectuando en el numerador: x2 – x – 6 - (x2 + 2x - 8) > 0
(x + 4) (x + 2)
x2 – x – 6 - x2 - 2x + 8 > 0
Página 99 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
(x + 4) (x + 2)
Simplificando:
-3x + 2
(x + 4) (x + 2)
>
0
Multiplicando por (-1) la desigualdad:
3x - 2
>
(x + 4) (x + 2)
0
Igualamos a cero el numerador y denominador:
3x – 2 = 0 Æ x = 2
3
x + 4 = 0 Æ x = -4
x + 2 = 0 Æ x = -2
Llevando los valores de x a la recta:
-∞
+
-4
-
+
2
+∞
3
Por regla práctica los denominadores son abiertos y el numerador es cerrado.
Por lo tanto:
x∈
-2
< -∞; 4 >
∪
>
1
x2 – 2x –15
13. Resolver:
- 2 ; 2
3
1
_
x2 – x –2
Solución:
1
x2 – 2x –15
>
1
x2 – x –2
Todo al primer miembro:
_
1
x2 – 2x –15
-
1
x2 – x –2
> 0
m.c.m.: (x - 5) (x - 2) (x + 1) (x + 3)
Efectuando:
(x - 2) (x + 1) - (x - 5) (x + 3) > 0
(x - 5) (x - 2) (x + 1) (x + 3)
Simplificando:
x2 – x – 2 – (x2 – 2x – 15)
(x - 5) (x - 2) (x + 1) (x + 3)
>0
x2 – x – 2 – x2 + 2x + 15
(x - 5) (x - 2) (x + 1) (x + 3)
>0
x + 13
(x - 5) (x - 2) (x + 1) (x + 3)
>
0
Igualando a cero el numerador y denominador:
x
x
x
x
x
+ 3 = 0 Æ x = -3
–5=0 Æx=5
–2=0 Æx=2
+ 1 = 0 Æ x = -1
+ 3 = 0 Æ x = -3
Llevando los valores de x a la recta y teniendo en cuenta que los numeradores son cerrados y el
denominador es abierto.
-
+
-
Página 100 de 167
+
-
+
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
-∞
-13
-3
-1
De donde: x ∈ [ -13; -3 > ∪
14. Resolver: x – 1
x+4
<
2
5
+∞
< -1 ; 2 > ∪ < 5 ; ∞ >
x-3
x-2
Solución:
x–1
x+4
<
x-3
x–2
Pasando al primer miembro:
x–1
x+4
-
x–3 <0
x–2
(x – 1) (x – 2) – (x – 3) (x + 4) < 0
(x + 4) (x – 2)
x2 – 3x + 2 – (x2 + x – 12) < 0
(x + 4) (x – 2)
x2 – 3x + 2 – x2 - x + 12 < 0
(x + 4) (x – 2)
-4x + 14
(x + 4) (x – 2)
Multiplicando por (-1):
<0
4x - 14
(x + 4) (x – 2)
<0
Igualando a cero el numerador y denominador:
4x – 14 = 0
Æ x=7
2
x+4=0
x–2=0
Æ
Æ
x = -4
x=2
Graficando:
-∞
+
-4
De donde: x ∈ < -4; -2 > ∪
3x2 – 2x
x2 - 1
15. Resolver:
-2
+
7
2
+∞
[ 7/2 ; ∞ >
> 4
Solución:
3x2 – 2x
x2 - 1
> 4
Todo al primer miembro:
3x2 – 2x - 4
x2 - 1
Efectuando:
3x2 – 2x - 4 (x2 – 1)
x2 - 1
Simplificando:
-x2 – 2x + 4
x2 - 1
> 0
Multiplicando por (-1):
x2 + 2x - 4
x2 - 1
> 0
> 0
Igualando a cero el numerador y denominador:
x2 + 2x – 4 = 0, de donde a = 1; b = 2; c = -4
Página 101 de 167
> 0
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
(2)2– 4(1)(-4)
2(1)
Por fórmula: x = -2 ±
Luego:
x1 = -2 + 2
2
x2 = -2 - 2
2
=
20
=
2
5 = -1 +
5 = -1 -
-2 ±
-2 ± 2
2
5
5
x2 – 1 = 0 Æ x2 = 1 Æ x = + 1
Llevando los valores de x a la recta:
+
-∞
-1 -
5
De donde: x ∈ [ -1 16. Resolver: 32
+
-
-1
5 ; -1 > ∪
1
-1 + 5
[ 1 ; -1 +
2x+1 < (42x . 8x-3)
+
5 ]
2/5
Solución:
Pasando a base 2, eliminando el radical y el paréntesis:
32 2x+1 < (42x . 8x-3) 2/5
25 . 2(x+1)/2 < (24x . 23x-9)
2 (x+11)/2 < (27x-9) 2/5
2 (x+11)/2 < 2(14x-18) /5
2/5
Luego, por propiedad:
x + 11 <
2
Resolviendo:
5x + 55 < 28x – 36
-23x < -91
23x > 91
Por (-1):
23x > 91
x
> 91
23
17. Resolver: 32x-3 . 34-x
35x-1
Solución:
<
(32x-1)
14x – 18
5
x-2
Aplicando las propiedades algebraicas:
32x-3 . 34-x
35x-1
3-4x + 2 < 2
<
(32x-1)
x-2
2
2x – 3x – 2
De donde:
-4x + 2 < 2x2 – 3x – 2
Resolviendo:
2x2 + x – 4 > 0
Por fórmula:
x1 = -1 +
4
Página 102 de 167
33
+∞
5
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
x2 = -1 4
De donde:
18. Resolver:
x ∈
5
(x
33
-∞ ; -1 +
4
2
2
– 2x)
33
. 62510x
∪
>
2520
-1 -
33 ; ∞
4
3
625x . 31257
1252x
2
Solución:
Pasando a base 5 y efectuando las operaciones indicadas:
5
2
2
(x – 2x)
. 62510x
3
625x . 31257
>
2
2520
5
2
2
(x – 2x)
1252x
. 540x
3
54x . 535
>
2
540
5
56x
2
2
(x – 2x) + 40x - 40
>
3
54x
2
– 6x + 35
De donde:
(x2 – 2x)2 + 40x - 40
> 4x3 – 6x2 + 35
Efectuando:
x4 – 4x3 + 4x2 + 40x - 40 - 4x3 + 6x2 – 35 > 0
x4 – 8x3 + 10x2 + 40x - 75 > 0
Factorizamos por Ruffini:
3
1
5
1
1
-8
10
40
-75
3
-15
-15
75
-5
-5
25
0
5
0
-25
0
-5
0
x4 – 8x3 + 10x2 + 40x – 75 > 0
Luego:
(x - 3) (x - 5) (x2 - 5) > 0
Igualando a cada factor a cero:
x–3=0 Æ x=3
x–5=0 Æ x=5
x2 – 5 = 0 Æ x = + 5
Graficando:
+
-∞
-5
De donde: x ∈ < - ∞; -
Página 103 de 167
+
5
5> ∪
3
[ 7/2 ; ∞ >
+
5
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
19. Resolver: (27) 3x
2
– 5x
< 81x . 92x-5
Solución:
2
27 . 3x
3
– 5x
< 81x . 92x-5
2
x – 5x
< 34 . 34x-10
3 . 3
2
x – 5x + 3
< 38x-10
3
x2 -5x + 3 < 8x – 10
x2 – 13x + 13 < 0
Por fórmula:
x1 = -13- 3 13
2
x2 = 13+ 3 13
2
De donde:
x ∈
20. Resolver:
4
13 - 3
2
13 ; 13 + 3
2
(0.8)(3x-4)/4
>
8
13
(0.64)(2x-2)/5
Solución:
4
(0.8)(3x-4)/4
>
8
(0.64)(2x-2)/5
Eliminando radicales:
(0.8)(3x-4)/16
Expresando en la misma base: (0.8)(3x-4)/16
Luego por propiedad:
3x – 4
16
Factorizando:
3x – 4
16
Simplificando:
Efectuando:
<
<
>
>
(0.64)(2x-2)/40
(0.8)2 [ (2x-2)/40 ]
2 . 2x – 2
40
4 (x – 1)
40
3x – 4
< x–1
16
10
3x – 4
< x–1
8
5
5 (3x - 4) < 8 (x - 1)
15x – 20 < 8x - 8
Transponiendo y simplificando:
7x < 12
x < 12
7
∴ x ∈ < - ∞; 12/7 >
21. Resolver: (0.25)(6x-4)/3.(0.5) (2x-3)/4<(0.0625) (3x-4)/6.(0.125) (4x-2)/9
Solución:
(0.25)(6x-4)/3 . (0.5) (2x-3)/4 < (0.0625) (3x-4)/6 . (0.125) (4x-2)/9
Escribiendo adecuadamente:
(0.5)(12x-8)/3 . (0.5) (2x-3)/4 < (0.5) (6x-8)/3 . (0.5) (4x-2)/3
Simplificando:
(0.5)[(12x-8)/3 ] + [ (2x-3)/4 ] < (0.5) [(6x-8)/3] + [(4x-2)/3]
Por propiedad:
12x – 8 + 2x – 3 > 6x – 8 + 4x – 2
3
4
3
3
48x – 32 + 6x – 9 > 24x – 32 + 16x – 8
Simplificando:
14x > 1 Æ x > 1/14 Æ x ∈ < 1/14, ∞ >
Página 104 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
(x+1)(x-2)
22. Resolver: [ (0.2)
]
1/(x-3)
(0.0128)3x-1
83x-1
>
Solución:
[ (0.2)
(x+1)(x-2)
]
1/(x-3)
>
(0.0128)3x-1
83x-1
……(I)
Aplicando propiedades:
0.0128 = 0.0128 x 104 =
128
= 16 = 24 = (0.2)4 en (I)
8
8 x 104
8 x 104
104
104
Por propiedad:
(0.2) [(x+1)(x-2)] / x-3
> [ (0.2)4 ]3x - 1
(0.2) [(x+1)(x-2)] / x-3
>
(0.2)12x - 4
Escribiendo adecuadamente: (x + 1) (x - 2)
x-3
Resolviendo:
<
12x – 4
(12x – 4) (x - 3) – (x + 1) (x – 2) > 0
x–3
11x2 – 39x + 14
x–3
>0
Igualando a cero numerador y denominador:
11x2 – 39x + 14 = 0 Æ
(39)2 - 4(11) (14)
2(11)
x = 39 ±
De donde:
x1 = 39 - 905
22
x2 = 39 + 905
22
Luego ubicando sobre la recta y graficando:
-∞
+
-
39 - 905
22
De donde:
23. Resolver:
x
∈
3
39 - 905 ; 3
22
x2 – 5
∪
+
39 + 905
22
39 +
+∞
905; ∞
22
> 2x + 3
Solución:
x2 – 5
i)
> 2x + 3
x2 – 5 > 0
x2 > 5 Æ x >
P(x) > 0:
Luego: x ∈ < - ∞ ; - 5 ] ∪ [
ii)
5 ∪ x < -
5;∞>
5
…… (α)
Q(x) > 0 ∧ P(x) > Q2 (x)
2x + 3 > 0
x >- 3
2
∧
∧
x2 – 5 > (2x + 3)2
x2 – 5 > 4x2 + 12x + 9
3x2 + 12x + 14 < 0
Luego su determinante es: ∆ = (12) 2 – 4(3)(14) = -24
Página 105 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Entonces reemplazamos: 3x2 + 12x + 14 por 1.
Así: 1 < 0, lo cual es falso ∴ x ∈ ∅
Entonces:
x >-3 ∧∅ Æ
2
x ∈ ∅ ………(β)
iii) Q(x) < 0 : 2x + 3 < 0 Æ x < - 2 ……… (γ)
3
iv) Finalmente: C.S.: α ∩ (β ∪ γ)
( < - ∞; - 5 ] ∪ [ 5; ∞ > ) ∩ (∅ ∪ < - ∞ ; - 3/2 > )
( < - ∞; - 5 ] ∪ [ 5; ∞ > ) ∩ < - ∞ ; - 3/2 >
De donde: x ∈ < - ∞ ; 24. Resolver:
2 + x – x2
5]
>
x-4
Solución:
i)
P(x) > 0:
2 + x - x2
> 0
Por (-1) :
x2 – x – 2
< 0
Factorizando:
(x – 2) (x + 1) < 0
Graficando:
+
-∞
-1
+
2
De donde: x ∈ [ -1; 2 ] …… (α)
ii)
Q(x) > 0 ∧ P(x) > Q2 (x)
x-4>0
x >4
2 + x - x2 > (x - 4)2
2 + x - x2 > x2 - 8x + 16
2x2 - 9x + 14 < 0
Como el ∆ < 0, entonces:
1 < 0 Falso
Luego: x > 4 ∧ ∅ de donde x ∈ ∅ (β)
iii) Q(x) < 0 : x - 4 < 0
x < 4 Æ x ∈ < - ∞ ; 4 > …… (γ)
iv) C.S.: α ∩ (β ∪ γ)
[ -1 ; 2 ] ∩ [ ∅ ∪ < - ∞ ; 4 > ]
[ -1 ; 2 ] ∩ < - ∞ ; 4 >
De donde: x ∈ [ -1 ; 2 ]
Página 106 de 167
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
x2 – 2x + 15
25. Resolver:
> x+1
Solución:
i)
x2 – 2x - 15 > 0
(x – 5) (x + 3) > 0
P(x) > 0:
Graficando:
+
-∞
-1
5
De donde: x ∈ < -∞ ; -3 ]
ii)
+
+∞
∪ [ 5 ; ∞ > …… (α)
Q(x) > 0 ∧ P(x) > Q2 (x)
x2 - 2x – 15 > (x + 1)2
x2 - 2x – 15 > x2 + 2x + 1
4x < - 16
x < -4
x+1>0
x > -1
Luego: x > -1
∧ x < -4 nos da x ∈ ∅ ……(β)
iii) Q(x) < 0 : x + 1 < 0
x < -1 Æ x ∈ < - ∞ ; -1 > …… (γ)
iv) C.S.: α ∩ (β ∪ γ)
< - ∞ ; -3 ] ∪ [ 5 ; ∞ > ) ∩ ( ∅ ∪ < - ∞ ; -1 > )
< - ∞ ; -3 ] ∪ [ 5 ; ∞ > ) ∩ < - ∞ ; -1 >
De donde: x ∈ < - ∞ ; -3 ]
x2 – x - 2
26. Resolver:
< 5-x
Solución:
i)
x2 – x - 2 > 0
(x – 2) (x + 1) > 0
P(x) > 0:
Graficando:
+
-∞
-1
De donde: x ∈ < -∞ ; -1 ]
ii)
+
2
+∞
∪ [ 2 ; ∞ > …… (α)
Q(x) > 0 ∧ P(x) > Q2 (x)
x2 - x – 2 > (5 - x)2
x2 - x – 2 > 25 – 10x + x2
9x < 27
x <3
5-x>0
x >5
Luego: x < 3
∧ x ∈ < -∞ ; 3 >……(β)
iii) C.S.: α ∩ β: ( < -∞ ; -1 ] ∪ [ 2 ; ∞ > ) ∩ < -∞ ; 3 >
De donde: x ∈ < - ∞ ; -1 ] ∪ [ 2 ; ∞ >
Página 107 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
x2 – 2x - 15
27. Resolver:
< 2x - 1
Solución:
i)
x2 – x - 15 > 0
(x – 5) (x + 3) > 0
P(x) > 0:
Graficando:
+
-∞
-3
De donde: x ∈ < -∞ ; -3 ]
ii)
+
5
+∞
∪ [ 5 ; ∞ > …… (α)
Q(x) > 0 ∧ P(x) > Q2 (x)
2x - 1 >
2x - 1 >
x >
Como ∆ < 0,
0
x2 - 2x – 15 < (2x - 1)2
0
x2 - 2x – 15 < 4x2 - 4x + 1
1/2
3x2 - 2x + 16 > 0
entonces 1 > 0 lo cual es verdadero.
Æ x∈R
Luego: x > 1/2
∧ x ∈ R tenemos x ∈ [ ½ ; ∞ >……(β)
iii) C.S.: α ∩ β: ( < -∞ ; -3 ] ∪ [ 5 ; ∞ > ) ∩ < ½ ; ∞ >
De donde: x ∈ [ 5 ; ∞ >
28. Resolver:
x2 – 9
< 4
Solución:
i)
x2 – 9 > 0
x2 > 9 Æ x > 3 ∪ x < -3
P(x) > 0:
De donde: x ∈ < -∞ ; -3 ]
ii)
Q(x) < Q2 (x);
∪ [ 3 ; ∞ > …… (α)
no es necesario hacer la restricción para Q(x)
porque es un número positivo.
x2 – 9 < 16
x2 < 25 Æ -5 < x < 5 de donde x ∈ < -5; 5 > ……(β)
iii) C.S.: α ∩ β: ( < -∞ ; -3 ] ∪ [ 3 ; ∞ > ) ∩ < -5 ; 5 >
Entonces: x ∈ < -5 ; -3 ] ∪ [ 3 ; 5 >
29. Resolver:
2x – 5
> 4
Solución:
i)
P(x) > 0:
2x – 5 > 0
x > 5/2
De donde: x ∈ [ 5/2 ; ∞ > …… (α)
ii)
Q(x) < Q2 (x);
no es necesario hacer la restricción para Q(x)
porque es un número positivo.
2x – 5 > 16
2x > 21
x > 21/2; de donde x ∈ < 21/2; ∞ > ……(β)
Página 108 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
iii) C.S.: α ∩ β: [ 5/2 ; ∞ > ∩ < 21/2 ; ∞ >
Entonces: x ∈ < 21/2 ; ∞ >
30. Resolver: | x – 4 |2 – 5 | x – 4 | + 6 = 0
Solución:
Hacemos:
| x – 4 | = y; con y > 0
Entonces:
| x – 4 |2 – 5 | x – 4 | + 6 = 0
Nos queda:
y2 – 5y + 6 = 0
Factorizando:
(y – 3) (y – 2) = 0
De donde:
y = 3; y = 2
Reemplazando:
|x–4|=3
|x–4|=2
De donde:
x–4=4
x=7
ó
ó
x – 4 = -3
x=1
x–4=2
x=6
ó
ó
x – 4 = -2
x=2
Luego: x = { 1 ; 2 ; 6 ; 7}
31. Resolver: ||x+2| - 1|2 – 5 ||x+2| -1 | -6 = 0
Solución:
Hacemos:
|| x + 2 | -1 | = y;
Entonces:
|| x + 2 | – 1 |2 - 5 ||x+2|-1| -6= 0
Nos queda:
y2 – 5y - 6 = 0
Factorizando:
(y – 6) (y + 1) = 0
De donde:
y = 6; y = -1
Reemplazando:
De donde:
|| x + 2 | - 1| = 6
|x + 2| - 1 = 6
ó
|x + 2| - 1 = -6
|x + 2| = 7
ó
|x + 2| = -5
x+2=7
x=5
ó
y>0
absurdo
x + 2 = -7
x = -9
Finalmente: x = { -9 ; 5}
32. Resolver: |x|+2|x- 1|– |2x-5| = 3
Solución:
a. Se igualan a cero las cantidades que están dentro del valor absoluto y los valores de x hallados
se llevan a la recta de los números reales:
Así: x = 0; x –1 = 0 Æ x = 1; 2x – 5 = 0 Æ x = 5/2
Graficando:
-∞
0
1
5/2
+∞
Los intervalos determinados se consideran de la siguiente forma:
Página 109 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
< - ∞ ; 0 ] ∪ < 1 ; 5/2 ] ∪ < 5/2 ; ∞ >
Se trabaja intervalos por intervalo empezando por el primer intervalo en este caso: < - ∞ ; 0 ],
se toma un x entre - ∞ y 0, se reemplaza en el valor absoluto de la ecuación original, si resulta
negativo se saca del V.A. tal como está:
Para: < - ∞ ; 0 ] …… (α)
Tomando un x del intervalo (x = -1), reemplazando en la inecuación inicial y aplicando la regla
anterior resulta:
- x + 2 (- x + 1) – (-2x + 5) = 3
- x – 2x + 2 + 2x – 5 = 3
-x=6
x = -6 Æ { -6 } ……… (β)
Luego: α ∩ β: { -6 } ……… (I)
Para: < 0 ; 1 ] …… (γ)
Tomamos: x = 0.5
x + 2 (- x + 1) – (-2x + 5) = 3
x – 2x + 2 + 2x – 5 = 3
x = 6 ……… (ψ)
Luego: γ ∩ ψ: ∅ ……… (II)
Para: < 1 ; 5/2 ] …… (α)
Tomamos: x = 2
x + 2 (x - 1) – (-2x + 5) = 3
x + 2x - 2 + 2x – 5 = 3
5x = 10
x = 2 Æ { 2 } ……… (β)
Luego: α ∩ β: { 2 } ……… (III)
Para: < 5/2; ∞] …… (γ)
Tomamos: x = 3
x + 2 ( x + 1) – (2x + 5) = 3
x + 2x - 2 - 2x + 5 = 3
x = 0 Æ { 0 } ……… (ψ)
Luego: γ ∩ ψ: ∅ ……… (IV)
Finalmente: C.S. I ∪ II ∪ III ∪ IV
{-6} ∪ ∅ ∪ {2} ∪ ∅ = { -6 ; 2 }
33. Resolver: |x2 – 9| + |x2 – 4| = 5
Solución:
Análogamente al ejemplo anterior:
x2 – 9 = 0 Æ x = + 3
x2 – 4 = 0 Æ x = + 2
-∞
-3
-2
2
Para: <-∞ ; -3 ] …… (α)
Tomamos: x = -4
x 2 – 9 + x2 – 4 = 5
2x2 = 18
x2 = 9 Æ
x=+3
Luego: { -3 ; 3 ] ……… (β)
Página 110 de 167
3
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
α ∩ β: { 3 } ……… (I)
Para: < -3; -2 ] …… (α)
Tomamos: x = -2.5
-x2 + 9 + x2 – 4 = 5
5=5
De donde: x ∈ R ……… (β)
Luego: α ∩ β: < -3 ; 2 ]……… (II)
Para: < -2; 2 ] …… (α)
Tomamos: x = 0
-x2 + 9 + x2 + 4 = 5
2x2 = 8
x = + 2 Æ { -2 ; 2 } ……… (β)
Luego: α ∩ β: { 2 } ……… (III)
Para: < 2; 3 ] …… (α)
Tomamos: x = 2.5
-x2 + 9 + x2 – 4 = 5
5=5
De donde: x ∈ R ……… (β)
Luego: α ∩ β: < 2 ; 3 ]……… (IV)
Para: < -3; ∞ ] …… (α)
Tomamos: x = 4
x 2 + 9 + x2 – 4 = 5
2x2 = 18 Æ x = + 3
De donde: { -3 ; 3 } ……… (β)
Luego: α ∩ β: ∅ ……… (V)
Finalmente: C.S. I ∪ II ∪ III ∪ IV ∪ V
{-3} ∪ < 3 ; 2 ] ∪ {2} ∪ < 2 ; 3 ] ∪ { -3 ; 3} = [ -3 ; -2 ] ∪ [ 2 ; 3 ]
34. Resolver: 2|x+2| - |2x+1 – 1| = 2x+1 + 1
Solución:
x + 2 = 0 Æ x = -2
2x+1 – 1 = 0
2x+1 = 2°
Entonces:
x+1=0
x=-1
Graficando:
-∞
-2
Para: < - ∞ ; -2 ] …… (α)
Tomando: x = -3
2-x-2 – (-2x+1 + 1) = 2x+1 + 1
2-x-2 + 2x+1 - 1 = 2x+1 + 1
2-x-2 = 21
-x–2=1
x = -3 Æ { -3 } ……… (β)
Página 111 de 167
-1
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Luego: α ∩ β: { - 3} ……… (I)
Para: < -2 ; -1 ] …… (α)
Tomando: x = -1.5
2x+2 – (-2x+1 + 1) = 2x+1 + 1
2x+2 + 2x+1 - 1 = 2x+1 + 1
2-x-2 = 21
x+2=1
x = -1 Æ { -1 } ……… (β)
Luego: α ∩ β: { - 1} ……… (II)
Para: < - 1 ; ∞ > …… (α)
Tomando: x = 0
2x-2 – (-2x+1 - 1) = 2x+1 + 1
2x+2 + 2x+1 + 1 = 2x+1 + 1
2x+2 = 2x-2
x+2=x+2 Æ
0= 0
Luego: x ∈ R …… (β)
Luego: α ∩ β: < - 1 ; ∞ > ……… (III)
Finalmente: C.S. I ∪ II ∪ III: [ -1 ; ∞ > ∪ { -3 }
35. Resolver: |3x – 1| < 5
Solución:
i.
ii.
iii.
3x – 1 < 5 Æ 3x < 6 Æ x < 2 ……(α)
3x – 1 > 5 Æ 3x > -4 Æ x > - 4/3 ……(β)
C.S.: α ∩ β
x ∈ [ -4/3 ; 2 ]
36. Resolver:
3x + 7
x–1
<
5
Solución:
1)
3x + 7 < 5
x–1
2) 3x + 7 > -5
x-1
3x + 7 – 5 < 0
x–1
3x + 7 + 5 > 0
x–1
3x + 7 – 5x + 5 < 0
x–1
- 2x + 12 < 0
x–1
2x – 12 > 0 …… (I)
x–1
3x + 7 + 5x - 5 > 0
x–1
8x + 2 > 0 …… (II)
x–1
Graficando (I)
+
-∞
1
De donde: x ∈ < -∞ ; 1 ]
Página 112 de 167
+
6
∪ [ 6 ; ∞ > …… (α)
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Graficando (II)
+
-
+
-∞
-1/4
1
De donde: x ∈ < -∞ ; - 1/4 ] ∪ [ 1 ; ∞ > …… (β)
+∞
3) α ∩ β: C.S. ( < -∞ ; 1 > ∪ < 6; ∞> ) ∩ ( < -∞ ; -1/4 > ∪ < 1; ∞ > )
Finalmente: x ∈ < -∞ ; - 1/4 ]
37. Resolver:
∪[6;∞>
1
(x+1) (x-2)
< 1
Solución:
1)
1
(x+1) (x-2)
<1
2)
1
–1<0
(x+1) (x-2)
1
(x+1) (x-2)
> -1
1
+1>0
(x+1) (x-2)
1 – x2 + x + 2 < 0
(x+1) (x-2)
x2 – x – 3 > 0 …… (I)
(x+1) (x-2)
x2 - x – 1 > 0 …… (II)
(x+1) (x-2)
Graficando (I)
+
-
+
-1
1- 13
2
3
De donde: x ∈ -∞ ; 1 - 13
2
2
-∞
+
1+ 13
2
∪ < -1 ; 2 > ∪
+∞
1 + 13
2
…… (α)
Graficando (II)
+
-
-∞
-1
+
1- 5
2
De donde: x ∈ <-∞ ;-1 > ∪
1+ 5
2
+
2
1- 5 ;1+ 5
2
2
+∞
∪
< 2 ; ∞ > …… (β)
3) C.S.: α ∩ β
Finalmente:
De donde: x ∈
-∞ ; 1 - 13
2
∪
1- 5;1+ 5
2
2
38. Resolver: | x + 1/x | < 6
Solución:
Se puede escribir de la siguiente forma:
x2 + 1
x
< 6
1) x2 + 1 < 6
x
Página 113 de 167
2) x2 + 1 > -6
x
∪
1 + 13; ∞
2
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
x2 + 1 – 6 < 0
x
x2 + 1 + 6 > 0
x
x2 – 6x + 1 < 0…… (I)
x
x2 + 1 + 6x > 0 …… (II)
x
Graficando (I)
-∞
+
-
0
3 –2
+
2
3+2 2
+∞
De donde: x ∈ < - ∞ ; 0 > ∪ [ 3 – 2 2; 3 + 2 2 ] …… (α)
Graficando (II)
-∞
0
+
- 3 –2
2
3+2 2
+
0
+∞
De donde: x ∈ < - 3 –2 2 ; -3 + 2 2 ] ∪ < 0 ; ∞ >
3) C.S. 3) C.S.: α ∩ β
Finalmente:
x ∈ [ - 3 –2 2 ; -3 + 2 2 ] ∪ [ 3 –2 2 ; 3 + 2 2 ]
39. Resolver: |3x – 7| > x – 3
Solución:
3x – 7 > x – 3
2x > 4
x>2
ó
3x – 7 < - (x – 3)
4x < 10
x < 5/2
∴x ∈ R
40. Resolver: |x2 + 3x | + x2 – 2 > 0
Solución:
|x2 + 3x | > x2 – 2
x2 + 3x > 2 - x2
2
2x + 3x - 2 > 0
+
-∞
x2 + 3x < - (2 - x2)
3x < -2
x < -2/3
ó
-
+
-2
x ∈ < - ∞ ; - 2/3 ] ∪ [ 1/2 ; ∞ >
41. Resolver:
½
+∞
3
– 2 (2x + 1) > 0
x+2
Solución:
3
– 2 (2x + 1) > 0
x+2
3
> 2x + 1
Página 114 de 167
ó
3
< -(2x+ 1)
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
x+2
x+2
3 – (2x + 1) 8x + 2) > 0
x+2
3 + (2x + 1) 8x + 2) < 0
x+2
∆<0
3 – 2x2 – 5x - 2 > 0
x+2
2x2 + 5x + 5) < 0
x+2
2x2 + 5x – 1 > 0
x+2
1
<0
x+2
x+2<0
-∞
+
+-
-5- 33
4
De donde: x ∈
-2
5+ 33
4
- ∞ ;-5 + 33
4
C.S. = x ∈ < - ∞ ; 2 > ∪
42. Resolver:
+
∪
-2 ; -5 + 33
4
+∞
∪ x < -2
-2 ; -5 + 33
4
5x + 2 - 2 > 0
x
Solución:
5x + 2 > 2
x
5x + 2 - 2
x
ó
>0
5x + 2 < -2
x
5x + 2 + 2 < 0
x
5x + 2 – 2x > 0
x
5x + 2 + 2x < 0
x
3x + 2 > 0
x
7x + 2 < 0
x
x ∈ < - ∞ ; - 2/3 > ∪ < 0 ; ∞ > ∪ x ∈ < - 2/7 ; 0 >
C.S. = x ∈ < - ∞ ; - 2/3 > ∪ < - 2/7 ; 0 > ∪ < 0 ; ∞ >
43. Resolver:
||||x2 + 1| - 1 | + 2 | - 3 | > 2x - 1
Solución:
Como x2 + 1 > 0, entonces:
||||x2 + 1| - 1 | + 2 | -3 > 2x – 1
Se escribe así,
|||x2 + 1 - 1 | + 2 | -3| > 2x – 1
Reduciendo:
|||x2 | + 2 | -3 | > 2x – 1
Como x2 > 0, entonces:
||x2 + 2| - 3 | > 2x – 1
Como x2 + 2 > 0, entonces:
|x2 + 2 - 3 | > 2x – 1
Reduciendo:
|x2 - 1 | > 2x – 1
Página 115 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Luego:
x2 – 1 > 2x – 1
x2 – 2x > 0
x (x – 2) > 0
x2 – 1 < - (2x – 1)
x2 – 1 < -2x + 1
x2 + 2x – 2 < 0
∨
Graficando
+
-∞
0
+
2
3
+∞
De donde: x ∈ < ∞ ; 0 > ∪ < 2 ; ∞ >
+
-∞
-1- 3
+
-1+
De donde: x ∈ < -1 - 3 ; - 1 +
3
+∞
3>
Finalmente: C.S.: x ∈ < -∞ ; -1 + 3 > ∪ < 2 ; ∞ >
44. Resolver:
1
x+4
∈ [1/3 , 1]
Solución:
1/3 ≤
1
< 1
x+4
1 ≤ x+4 ≤3
=> -3 ≤ x ≤ -1 luego la solucion es: x ∈ [-3 , -1]
45. Resolver:
5
≥
2x – 1
1
x-2
Solución:
5
2x – 1
se tiene:
≥
1
x–2
ÅÆ
5
≥
2x – 1
1
x-2
para x ≠ 1/2
5 |x-2| ≥ |2x-1| elevando al cuadrado
25 (x-2)2 ≥ (2x-1)2 efectuando y simplificando
7x2 – 32x + 33 ≥ 0 ÅÆ (7x-1)(x-3) ≥ 0
+
11/7
0
+
3
Como (7x-1)(x-3) ≥ 0, se toma los intervalos donde aparece el signo (+), es decir:
< -∞ , 11/7 ] U [ 3 , +∞ >
Página 116 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
46. Resolver:
2 2 – 10 |x| - 16 – x2
-3 + x – 2
- 9–x > 0
x-8
Solución:
Efectuando las restricciones:
x – 2 > 0 ∧ 10|x| - 16 – x2 > 0 ∧
A
De A: x > 2
10 |x| - 16 – x2 > 0
-3 + x – 2
2 2–
B
C
De B: como: x > 2 Æ |x| = x
10|x| - 16 – x2 > 0
10x - 16 – x2 > 0
Por (-1):
x2 -10x – 16 < 0
(x - 8) (x - 2) < 0
De donde:
x–8=0Æx=8
x–2=0Æx=2
Graficando:
+
-∞
2
+
8
+∞
Entonces: x ∈ [ 2 ; 8 ] ………(I)
De C: como: x ∈ [ 2 ; 8 ] Æ
2<
x
<8
0<
x–2
<6
0<
x–2
<
-3 <
x–2–3 <
6
6-3
De donde se deduce que ( x – 2 – 3) es negativo, entonces en:
2 2–
10 |x| - 16 – x2 > 0
-3 + x – 2
El numerador debe ser menor o igual que cero, es decir,
2 2–
10 |x| - 16 – x2 < 0, como |x| = x
10x - 16 – x2 > 2 2
10x – 16 – x2 > 8
x2 – 10x + 24 < 0
(x – 6) (x - 4) < 0
Graficando:
+
-∞
Entonces: x ∈ [ 4 ; 6 ]
4
Luego, la restricción es: x ∈ [ 4 ; 6 ]
Trabajando en la expresión inicial:
Página 117 de 167
+
6
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
2 2 – 10 |x| - 16 – x2
-3 + x – 2
- 9–x > 0
x-8
……… (α)
De: x ∈ [ 4 ; 6]
4<
x < 6 multiplicando por (-1);
-6 < -x < -4 sumando 9
3<9–x<5 ∴9–x >0
De: x ∈ [ 4 ; 6]
x < 6 restando 8
4<
-4 < x - 8 < -2 ∴ x – 8 < 0
Entonces :
9–x<0
x–8
Entonces la solución de α es solamente la solución de la restricción de la raíz; o sea:
x ∈ [ 4 ; 6]
47. Resolver:
x||x|-1|-12
|x+2|+1
-
||1-x|-3| |x-1|+4
x–9 >0
Solución:
x||x|-1|-12
|x+2|+1
-
||1-x|-3| |x-1|+4
x – 9 > 0 …… (I)
A
Efectuando la restricción: x – 9 > 0 Æ x > 9 …… (α)
De donde deducimos que:
|x|
|x + 2|
|1 - x|
|x - 1|
=
=
=
=
x
x+2
x–1
x–1
Reemplazando en A:
A = x |x – 1| - 12 x+2+1
|x – 1 – 3|
x–1+4
A = x |x – 1| - 12 x+3
|x – 4|
x+3
Como: x > 9, entonces:
|x - 4| = x – 4
|x - 1| = x – 1
= x (x – 1) – 12 – (x – 4)
x+3
= x2 - x – 12 – x + 4
x+3
= x2 - 2x – 8
x+3
= (x - 4) (x - 2) …… (II)
x+3
Reemplazando (II) en (I):
(x – 4) (x + 2)
x+3
Elevando al cuadrado:
>
x-9
(x – 4) (x + 2) - x – 9 > 0
x+3
(x - 4) (x + 2) – (x – 9) (x + 3) > 0
x+3
x2 – 2x + 8 - (x2 – 6x – 27) > 0
Página 118 de 167
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
x+3
De donde:
4X + 19 = 0 Æ
x+3=0 Æ
x = - 19/4
x = -3
Graficando:
+
-
-∞
+
- 19/4
1
+∞
De donde: x ∈ < - ∞ ; - 19/4 ] ∪ < 1 ; ∞ > …… (β)
Solución final: α ∩ β
x∈[9;∞>
48. Resolver: | x | - 9 | 4 x | + 18 > 0
Solución:
Restricción: x > 0 …… (α)
x + 18 > 9 4 x
Elevando al cuadrado: x + 36 x + 324 > 81 x
x + 324 > 45 x
(x + 324)2 > (45
Elevando al cuadrado:
x )2
x2 + 648x + 104.976 > 2025x
x2 – 1377x + 104.973 > 0
x = 1377 ± 1215
2
Æ x = 1396; x2 = 81
+
-∞
81
+
1396
De donde: x ∈ < - ∞ ; 81 ] ∪ [ 1396 ; ∞ > …… (β)
C.S.: α ∩ β Æ x ∈ [ 0 ; 81 ] ∪ [ 1396 ; ∞ >
Página 119 de 167
+∞
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
Problemas Propuestos
1.
Si x ∈ <2,4>, entonces
a)<7,11>
2.
1
2x+3
pertenece a:
b)[7,11] c)<1/7,1/11> d)<1/11,1/7> e) N.A.
Resolver: 5x – 9 = 3
2x + 3
Dar como respuesta la suma de las soluciones:
a) -18
3.
Resolver:
a) 2
4.
b) 18
c) 0
d) 15
e) -15
|x – 1|2 + 2 |x – 1| + 1 = 0
b) 1
c) φ
d) Imposible
e) N.A.
Si x ∈ [ 1000, α > hallar “x” sabiendo que:
|x–1|+|1–x|+|x–2|+|2–x|+|x–3|+|3–x| +…… +
|x – 1000| + |1000 – x| = 106
a) 2001
6
5.
6.
Si
b) 1000
3
∈
3x – 4
c) 2001
2
d) 10000
e) N.A.
[ 1/15 , ¼ ], hallar el menor n
Tal que:
x + 2
x + 6
a) 43/67
b) 15/17
<
M
c) 10/9
d) 13/16
Hallar el conjunto de: (x - 1)2 (x – 6)
(x - 5)4
e) 15/19
< 0
a) <-∞,6> b) <-∞,6> - {5}
c) <-∞,6> - {1}
d) <-∞,6> - {1,5}
e) N.A.
7.
Hallar el conjunto de |2x + 3| > |3x – 5|.
Dar como respuesta la suma de los extremos
solución.
a) 42/5
8.
b) 27/5
c) 4/5
Hallar A si A’ = { x ∈ R /
d) 53/5
1/(x2+2x-13)
finitos
del
intervalo
e) 18/5
>
1/(x2+3x) }
Dar como respuestas la suma de los extremos finitos de los intervalos solución.
a) 16
9.
b) -18
c) 18
d) -16
e) 10
Hallar la inecuación racional más simple que tiene por solución:
< -1, -1/3 > ∪ < 7, ∞ >
a) (x-2)(x+1/3)<0
b)(3x–2)(x+7)(x–1)> 0
c) (x+1)(3x–1)(x+7)>0 d)(x+1)(3x+1)(x–7)> 0
e) (x+1)(3x+1)(x+7)> 0
10. Resolver:
a) [4,2]
|3x – x2| - 4
4 - |x|
b) <-4,2>
Página 120 de 167
>
-1
c) [-4,3>
d) <4,2]
e) N.A.
UNIVERSIDAD PRIVADA DE MOQUEGUA “JOSE CARLOS MARIATEGUI”
11. La suma de los elementos del conjunto solución de la ecuación:
|x - 2| + x2 = 4 es:
a) 1
b) 2
c) 3
d) 4
e) N.A.
12. Cuántos números enteros satisfacen la inecuación:
|x – 3| < 1
a) 2
b) 3
c) 4
d) 5
e) N.A.
13. Hallar “h” en |2x-h|<m, si es equivalente a:-2<x<3.
a) 2
b) 1
c) 4
d) 3
e) N.A.
d) 5
e) N.A.
14. Resolver: |x - 2| = -x + 6
Señalando: x
a) 7
x
b) 6
c) 8
15. Resolver: |x| - 2|x + 1| + 3 |x + 2| = 0
a) -4
b) 2
c) -2
d) -3
e) N.A.
16. Se sabe que el cuádruple del número de monedas que hay dentro de una
bolsa es tal, que disminuido en 5, no puede exceder de 31, y que el
quíntuplo del mismo número de monedas aumentando en 8, no es menor
que 52. ¿Cuál será dicho número?
a) 10
b) 9
c) 8
d) 7
e) N.A.
17. En un gallinero había un cierto número de gallinas. Se triplicó este
número y se vendieron 95, quedando menos de 87. Después se duplicó el
número de gallinas que había al principio y se vendieron 40, quedando
más de 79. ¿Cuántas gallinas había inicialmente en el gallinero?
a) 60
b) 62
c) 64
d) 66
e) N.A.
18. Hallar los valores de “x” que satisfacen a la limitación siguiente:
2x – 5 < x + 3 < 3x – 7
a) 5 < x < 8
d) 4 < x < 8
b) 5 < x < 10
e) N.A.
c) 4 < x < 11
19. Hallar el menor número “M” con la propiedad de que para todo:
x ∈ R: 1 + 6x – x2 < M
a) 8
b) 9
c) 10
d) 11
e) N.A.
20. Resolver la inecuación:
x2 – 4x + 6 < 0
a) x ∈ <-∞,5]
d) x ∈ < ∞, 6]
b) x ∈ [4,5]
e) N.A.
c) Inecuación Imposible
CLAVE DE RESPUESTAS:
1
2
3
4
5
6
7
8
9
d
a
c
c
a
c
a
b
d
b
11
12
13
a
b
b
14
15
c
c
Página 121 de 167
16
b
10
17
18
19
20
a
a
c
c