ACTIVIDAD #7 – CAMBIO VERTICAL Y ECUACIÓN DE UN PLANO

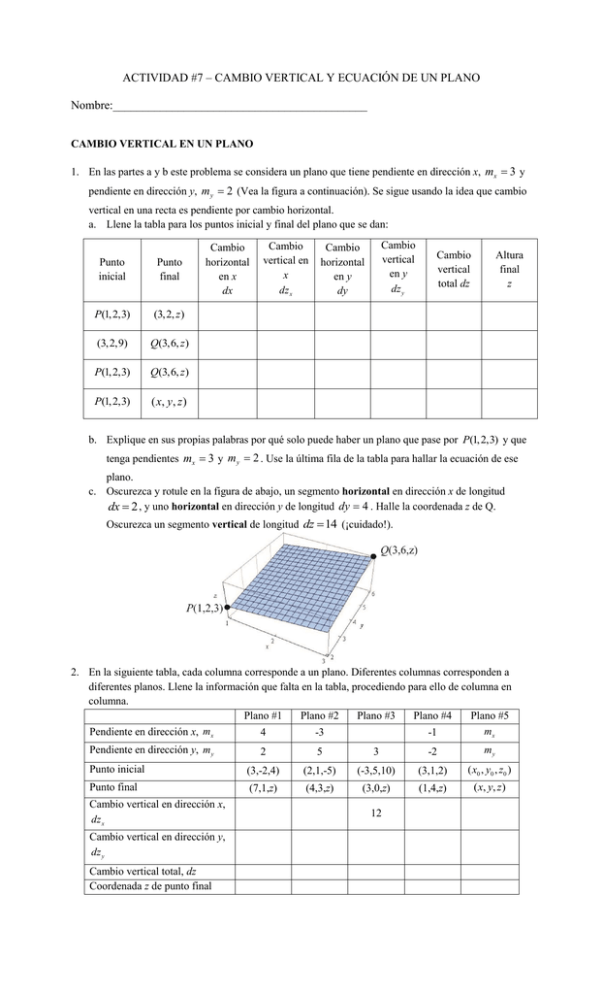
ACTIVIDAD #7 – CAMBIO VERTICAL Y ECUACIÓN DE UN PLANO
Nombre:___________________________________________
CAMBIO VERTICAL EN UN PLANO
1. En las partes a y b este problema se considera un plano que tiene pendiente en dirección x, mx  3 y
pendiente en dirección y, m y  2 (Vea la figura a continuación). Se sigue usando la idea que cambio
vertical en una recta es pendiente por cambio horizontal.
a. Llene la tabla para los puntos inicial y final del plano que se dan:
Punto
inicial
Punto
final
P(1, 2,3)
(3,2, z )
(3, 2,9)
Q(3,6, z )
P(1, 2,3)
Q(3,6, z )
P(1, 2,3)
( x, y , z )
Cambio
horizontal
en x
dx
Cambio
vertical en
x
dz x
Cambio
vertical
en y
dz y
Cambio
horizontal
en y
dy
Cambio
vertical
total dz
Altura
final
z
b. Explique en sus propias palabras por qué solo puede haber un plano que pase por P(1, 2,3) y que
tenga pendientes mx  3 y m y  2 . Use la última fila de la tabla para hallar la ecuación de ese
plano.
c. Oscurezca y rotule en la figura de abajo, un segmento horizontal en dirección x de longitud
dx  2 , y uno horizontal en dirección y de longitud dy  4 . Halle la coordenada z de Q.
Oscurezca un segmento vertical de longitud dz  14 (¡cuidado!).
2. En la siguiente tabla, cada columna corresponde a un plano. Diferentes columnas corresponden a
diferentes planos. Llene la información que falta en la tabla, procediendo para ello de columna en
columna.
Plano #1
Plano #2
Plano #3
Plano #4
Plano #5
mx
Pendiente en dirección x, mx
4
-3
-1
Pendiente en dirección y, m y
2
5
3
-2
my
Punto inicial
(3,-2,4)
(2,1,-5)
(-3,5,10)
(3,1,2)
( x0 , y0 , z0 )
Punto final
(7,1,z)
(4,3,z)
(3,0,z)
(1,4,z)
( x, y, z)
Cambio vertical en dirección x,
dz x
Cambio vertical en dirección y,
dz y
Cambio vertical total, dz
Coordenada z de punto final
12
ECUACIÓN DE UN PLANO
3. Reflexione sobre lo que hizo en la columna 5 del problema anterior. Suponga que tiene un plano que
pasa por un punto dado ( x0 , y0 , z0 ) y que tiene pendiente en dirección x, mx , y pendiente en
dirección y, m y (O sea, puede tratar a x0 , y0 , z 0 , mx , m y como si fuesen constantes). Halle el
cambio vertical desde el punto ( x0 , y0 , z0 ) hasta un punto genérico cualquiera ( x, y, z ) . Explique
por qué acaba de hallar la ecuación del plano. (La ecuación del plano es una ecuación que permite
expresar la coordenada z de cualquier punto en el plano en términos de las coordenadas x y y del
punto.)
4. Considere un plano con pendientes mx  4 , m y  3 y que pasa por el punto P (2, 1,5) . Suponga
que moviéndose sobre el plano, primero en dirección x y luego en dirección y se llega a un punto
genérico Q( x, y, z ) (vea la figura a continuación).
a. Oscurezca en la figura de abajo, segmentos horizontales de recta cuya magnitud sea igual a la
magnitud de dx  x  2 y de dy  y  (1) , y un segmento vertical con magnitud igual a la de
dz  z  5 (¡cuidado!).
b. Exprese el cambio vertical (dz) desde el punto dado P (2, 1,5) , hasta el punto genérico
Q( x, y, z ) en una ecuación que envuelva solamente las variables x, y, z. La ecuación que se
obtiene es la ecuación del plano.
5. Use el procedimiento del problema anterior para hallar la ecuación del plano que pasa por
P(3, 4, 1) y tiene pendientes mx  1 , m y  8 .
6. Halle la ecuación del plano representado en la figura a continuación:
11
z
8
3
5
2
0
y
1
1
x
2
3
0
7. Halle la ecuación del plano cuyo diagrama de contorno es como sigue:
8. Halle la ecuación del plano cuya tabla es como sigue:
0
3
6
2
18
20
22
4
15
17
19
6
12
14
16
y
x
9. Halle la ecuación del plano que pasa por (0,0,5) , (2,0,0) , (0, 1,0) .