7.3 Double-Angle and Half

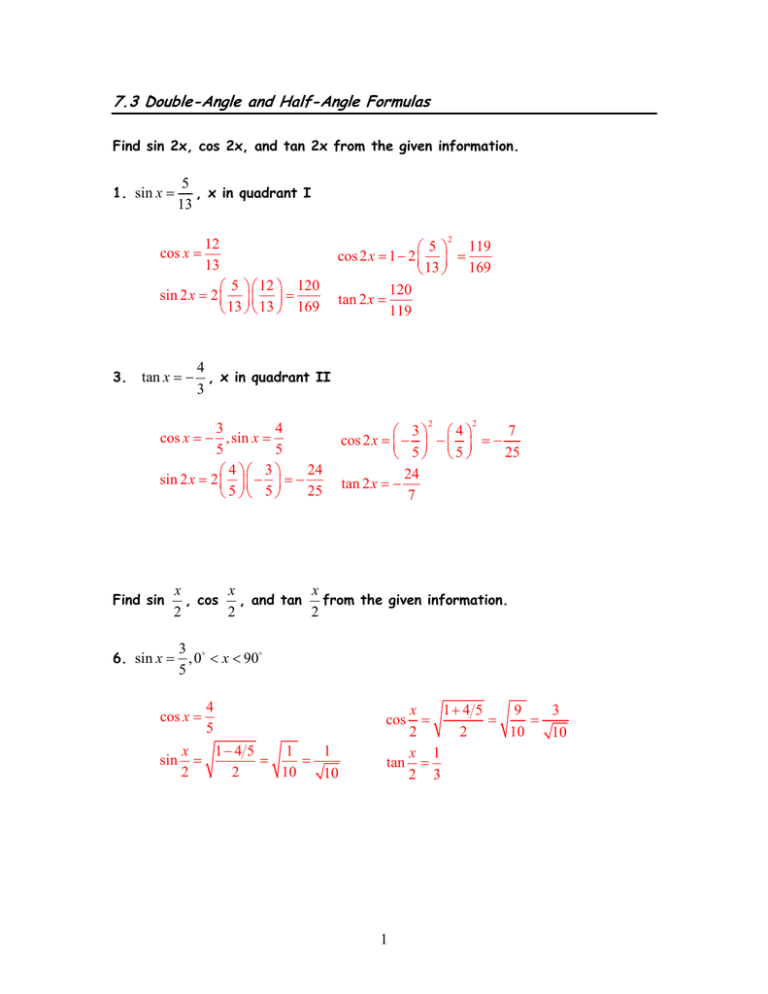
7.3 Double-Angle and Half-Angle Formulas
Find sin 2x, cos 2x, and tan 2x from the given information.
1. sin x =
5
, x in quadrant I
13
12
13
 5   12  120
sin 2 x = 2     =
 13   13  169
cos x =
3.
2
 5  119
cos 2 x = 1 − 2   =
 13  169
120
tan 2 x =
119
4
tan x = − , x in quadrant II
3
3
4
cos x = − , sin x =
5
5
24
 4  3 
sin 2 x = 2   −  = −
25
 5  5 
Find sin
2
2
7
 3  4
cos 2 x =  −  −   = −
25
 5 5
24
tan 2 x = −
7
x
x
x
, cos
, and tan
from the given information.
2
2
2
6. sin x =
3 , 0 < x < 90
5
cos x =
sin
4
5
x
1− 4 5
1
1
=
=
=
2
2
10
10
x
1+ 4 5
9
3
=
=
=
2
2
10
10
x 1
tan =
2 3
cos
1
9. sec x =
3
, 270 < x < 360
2
cos x =
sin
2
3
x
1+ 2 3
5
5
=−
=−
=−
2
2
6
6
x
1
tan = −
2
5
cos
x
1− 2 3
1
1
=
=
=
2
2
6
6
Use an appropriate half-angle formula to find the exact value of the
expression.
5π
12
 5π 
1 + cos ( 5π 6 )
1− 3 2
2− 3
2− 3
=
=
=
cos  6  =
 2 
2
2
4
2


15. cos
Use an appropriate double-angle formula to find the exact value of the
expression.
17. tan120
tan(2 ⋅ 60o ) =
2 tan 60o
2⋅ 3
=
2
o
1 − tan 60 1 − 3
( )
2
=
2
2 3
=− 3
−2