Solución modelo A

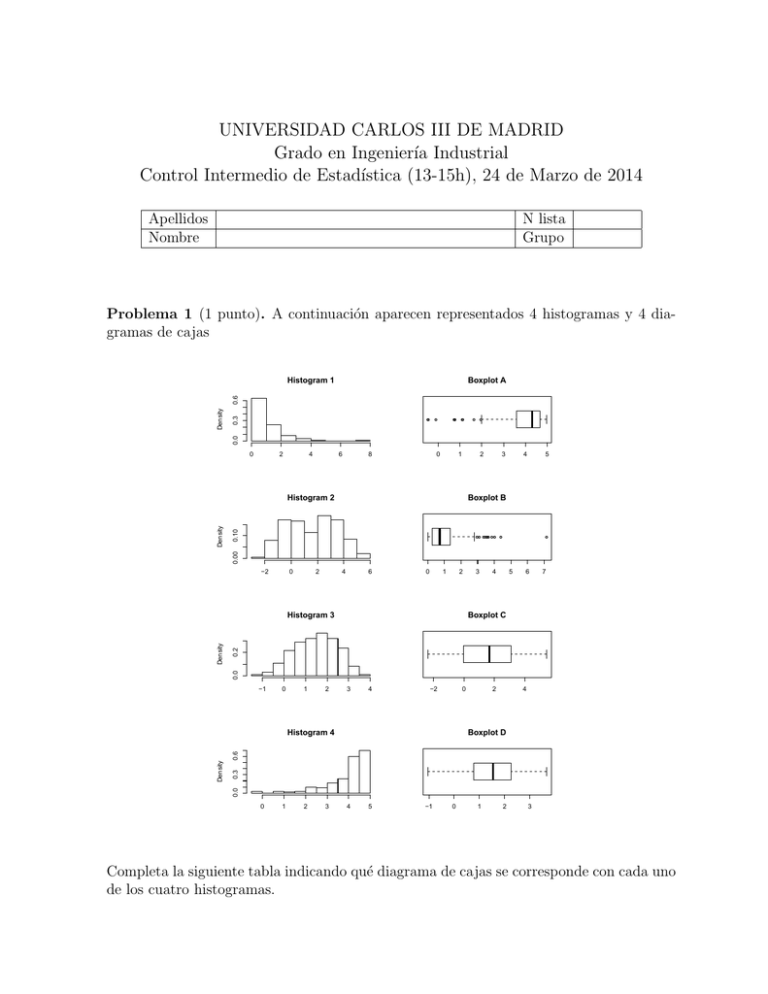
UNIVERSIDAD CARLOS III DE MADRID
Grado en Ingenierı́a Industrial
Control Intermedio de Estadı́stica (13-15h), 24 de Marzo de 2014
Apellidos
Nombre
N lista
Grupo
Problema 1 (1 punto). A continuación aparecen representados 4 histogramas y 4 diagramas de cajas
Boxplot A
0.3
●
●
●
●
●
●
●
●
●
0.0
Density
0.6
Histogram 1
0
2
4
6
8
0
1
2
4
5
0.10
Boxplot B
● ● ●●●● ● ●
●
●
0.00
Density
Histogram 2
3
−2
0
2
4
6
0
1
2
4
5
6
7
0.2
Boxplot C
0.0
Density
Histogram 3
3
−1
0
1
2
3
4
−2
0
4
0.3
0.6
Boxplot D
0.0
Density
Histogram 4
2
0
1
2
3
4
5
−1
0
1
2
3
Completa la siguiente tabla indicando qué diagrama de cajas se corresponde con cada uno
de los cuatro histogramas.
Histograma Diagrama de cajas
(Boxplot)
1
B
2
C
3
D
4
A
Problema 2 (2 puntos). Una pequeña fábrica de raquetas de pádel analiza el número
de raquetas defectuosas que se producen en un dı́a. Para ello durante un mes de 31 dı́as
anotan el número de raquetas defectuosas que se produjeron cada dı́a. La siguiente tabla
muestra las frecuencias absolutas de cada número de raquetas defectuosas.
Número de raquetas defectuosas
0
1
2
3
4
6
8
Número de dı́as
12
8
3
3
3
1
1
Frec.Acum.
12
20
23
26
29
30
31
Frec.R.
0.387
0.258
0.096
0.096
0.096
0.03
0.03
Frec.R.Acum.
0.387
0.645
0.741
0.838
0.935
0.967
1
Se pide:
a) La media, varianza y coeficiente de variación de raquetas defectuosas por dı́a.
media = x̄ =
P
var = s2 =
(xi − x̄)2 · f r(xi ) = 3.79.
P
xi f r(xi ) = 0 · 0.387 + 1 · 0.258 + 2 · 0.096 + . . . = 1.58.
√
C.V. =
s2
|x̄|
= 1.23.
b) Realizar un diagrama de cajas (boxplot) especificando cada uno de sus tres cuartiles.
2
Q1 = 0 (posición 8); Q2 = 1 (pos 16); Q3 = 3 (pos 17 + 7 = 24); IQR = 3;
1.5·IQR = 4.5.
●
0
2
4
6
8
Problema 3 (1 punto). Los sucesos A y B son independientes. Demuestra que
Pr (A ∩ B c ) = Pr (A) Pr (B c ) .
¿Son A y B c también independientes? Razona tu respuesta.
(α)
(β)
sol-1) Pr(A ∩ B̄) = Pr(B̄ ∩ A) = Pr(B̄|A) Pr(A) = (1 − Pr(B|A)) Pr(A)
(γ)
= (1 − Pr(B)) Pr(A) = Pr(B̄) Pr(A) = Pr(A) Pr(B̄)
sol-2) Pr(A ∩ B̄) = P (A) − P (A ∩ B) =
= P (A) − P (A)P (B) = P (A)(1 − P (B)) = P (A)P (B̄)
La relación que acabamos de probar demuestra que A y B c son independientes. Es
decir, el hecho de que B c ocurra (B no ocurra) no nos aporta ninguna información
sobre si A ocurre.
(α) : Definición de probabilidad condicional.
(β) : Pr(·|B) es una probabilidad.
(γ) : independencia de A y B.
Problema 4 (2 puntos). Tenemos dos urnas. La primera contiene dos bolas rojas y
cuatro bolas verdes, mientras que la segunda contiene tres bolas rojas y tres verdes.
Seleccionamos una de las urnas según el resultado del lanzamiento de una moneda cuya
probabilidad de cara es p = 1/3. Si sale cara, se selecciona la primera urna, mientras que
si sale cruz se selecciona la segunda. A continuación extraemos una bola al azar de la
urna seleccionada.
a) ¿Cuál es la probabilidad de extraer una bola roja?
3
R ≡ extraer una bola roja ;
V ≡ extraer una bola verde ;
u1 ≡ seleccionar la primera urna
u2 ≡ seleccionar la segunda urna
(α)
Pr(R) = Pr(R|u1 ) Pr(u1 ) + Pr(R|u2 ) Pr(u2 ) =
2 1 3 2
· + · = 0.444
6 3 6 3
(α) : Fórmula de la probabilidad total.
b) Si la bola extraı́da resultó ser verde, ¿cuál es la probabilidad de que proceda de la
primera urna?, ¿y la probabilidad de que proceda de la segunda?
(α)
Pr(u1 |V ) =
Pr(V |u1 ) Pr(u1 )
=
Pr(V |u1 ) Pr(u1 ) + Pr(V |u2 ) Pr(u2 )
Pr(u2 |V ) = 1 − Pr(u1 |V ) =
4
6
·
4 1
·
6 3
1
+ 63
3
·
2
3
=
2
= 0.4
5
3
= 0.6
5
(α) : Bayes.
Problema 5 (2.5 puntos). El tamaño de los tornillos que produce una determinada
máquina es una variable aleatoria X con una distribución normal de media 100mm y
desviación tı́pica 10mm. Únicamente son válidos los tornillos que tienen un tamaño entre
90mm y 110mm. Utilizando la salida de Statgraphics:
4
Se pide:
a) P (99 ≤ X ≤ 100)
Pr(X ≤ 100) − Pr(X < 99) = 0.50 − 0.46 = 0.04.
b) P (X = 100)
0.
c) P (99 ≤ X < 100)
Como en el apartado a), ya que Pr(X ≤ 100) = Pr(X < 100) dado que X sigue una
distribución continua.
d) ¿Cuál es la probabilidad que un tornillo sea defectuoso?
5
Pr(X < 90) + Pr(X > 110) = 0.158 + 0.158 = 0.316.
e) Si se coge una muestra de 10 tornillos cuál es la probabilidad de obtener al menos
un tornillo defectuoso?, ¿cuál es la probabilidad de obtener exactamente un tornillo
defectuoso?
Y ≡ número de tornillos defectuosos en una muestra de 10
Y ∼ Bin(n = 10, p = 0.316)
Pr(Y ≥ 1) = 1 − Pr(Y = 0) = 1 −
Pr(Y = 1) =
10
0
(0.316)0 (1 − 0.316)10 = 1 − 0.022 = 0.978.
10
1
(0.316)1 (1 − 0.316)9 = 0.10356.
Problema 6 (1.5 puntos). Dada una variable aleatoria continua X con función de densidad
(1/k)e−x/40 si x > 0
fX (x) =
.
0
si x ≤ 0
a) Calcular el valor de k.
Z
0
Z
∞
1 −x/40
e
dx = 1
k
e−x/40 dx = −40e−x/40 ⇒
∞
1
−40e−x/40 0 ⇒ k = 40
k
b) Calcular la esperanza y la probabilidad de que X tome valores entre 20 y 60.
6
Z
∞
Z
∞
1 −x/40
e
dx = 40.
40
x
xf (x)dx =
E[X] =
0
0
Z
60
Pr(20 ≤ X ≤ 60) =
Z
60
f (x)dx =
20
20
7
1 −x/40
e
dx = 0.383.
40