Estructura algorítmica de iteración

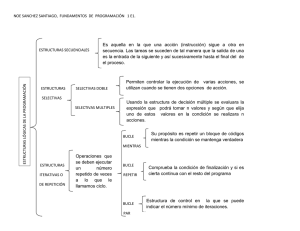
Estructura algorítmica de iteración
Las estructuras algorítmicas fundamentales son: secuenciación, selección e iteración.
También se las conoce como estructuras de control porque especifican el orden en
que los pasos de un algoritmo se ejecutarán. Este orden de ejecución de los pasos,
sentencias, o instrucciones, determinan el flujo de control de un algoritmo.
Las estructuras iterativas o repetitivas controlan el número de veces que una acción o
grupo de acciones deben ejecutarse. Un bucle o lazo, loop en inglés, es cualquier
construcción algorítmica que repite una acción o secuencia de acciones un número de
veces. A estas acciones le llamamos cuerpo del bucle, y cada repetición del cuerpo se
llama iteración del bucle.
Iteración condicional
Usamos una estructura algorítmica de iteración condicional cuando no sabemos de
ante mano cuántas veces vamos a repetir o iterar el cuerpo del bucle. En este tipo de
estructura de control encontramos los siguientes elementos:
inicialización: establece un valor inicial para aquellas variables que participan
en la condición booleana.
condición: es una expresión booleana que se evalúa como verdadero o falso,
según el valor de las variables que participan en esa condición con la cual se decide si
el cuerpo del bucle debe repetirse o no.
actualización: es una acción más del cuerpo del bucle que hace variar el valor
de las variables que forman partes de la condición. El cuerpo del bucle debe actualizar
la condición, sino generaríamos un lazo o bucle infinito. No necesariamente la
actualización se realiza en una sola acción, puede darse en varias acciones y ser tan
compleja como sea necesario, pero siempre dentro del lazo.
Mientras-Repetir:
En esta forma el cuerpo del bucle podría no
ejecutarse nunca ya que primero se evalúa la
condición.
inicialización
MIENTRAS(condición)REPETIR
A1
A2
:
cuerpo
AN
actualización
FIN MIENTRAS
Repetir-Hasta Que
Primero ejecuta el cuerpo del bucle y luego
actualiza las variables de la condición, por lo
tanto el cuerpo del bucle se ejecutará al
menos una vez.
inicialización
REPETIR
A1
A2
:
AN
actualización
HASTA QUE(condición)
cuerpo
Iteración de un número fijo de veces
Cuando sabemos el número de veces que debemos ejecutar un grupo de acciones es
acertado usar este tipo de estructura. La inicialización, actualización y condición están
representada de manera implícita en la propia estructura iterativa.
Hacer
La inicialización esta dada por la expresión
(i=1), la condición para este ejemplo sería
“i<=N”
y hacemos referencia a la
actualización con (+1) diciendo que el índice
i se incrementará en una unidad por cada
iteración. Todo esto existe de manera
implícita y forma parte de la estructura
iterativa HACER.
Podemos encontrar un equivalente del
ejemplo anterior en la forma MientrasRepetir. Se aconseja usar la estructura Hacer
cuando el número de veces a repetir es fijo y
no va a cambiar por las acciones que se
ejecuten en el cuerpo del bucle.
HACER(N)VECES (i=1,N,+1)
A1
A2
:
cuerpo
AN
FIN HACER
i ← 1
MIENTRAS(i<=N)REPETIR
A1
A2
:
AN
i ← i + 1
FIN MIENTRAS
Ejemplos de iteración
1- Encontrar el número más grande, más chico, y el número promedio de una
secuencia de enteros.
ALGORITMO
ENTRADA
SALIDA
VAR. AUX.
CONSTANTE
:
:
:
:
:
Máximo, mínimo y promedio
numero: entero de 4 cifras (secuencia de enteros con marca final)
máximo, mínimo, promedio: numero entero
total, cantidad: entero
MARCA_FINAL=-9999
inicializar variables
LEER(numero)
MIENTRAS(numero ≠ MARCA_FINAL)
cantidad ← cantidad + 1
total ← total + numero
encontrar máximo y mínimo
LEER(numero)
FIN MIENTRAS
escribir salida
PARAR
inicialización
condición
Cuerpo
del bucle
actualización
inicializar variables:
escribir salida:
máximo ← -10000
mínimo ← 10000
cantidad ← 0
total ← 0
SI(cantidad > 0)ENTONCES
promedio ← total / cantidad
ESCRIBIR(máximo, mínimo, promedio)
SINO
ESCRIBIR(“secuencia vacía”)
encontrar máximo y mínimo:
SI(numero > máximo)ENTONCES
máximo ← numero
SI(numero < mínimo)ENTONCES
mínimo ← numero
2- Se necesita saber el promedio de la suma de los factoriales de una secuencia de
números enteros no negativos donde el fin de la secuencia se indica con un número
negativo.
ALGORITMO
ENTRADA
SALIDA
VAR. AUX.
SUPUESTO
:
:
:
:
:
promedio de factoriales
num: entero positivos (secuencia de enteros)
promedioFactorial: numero entero
cant, factorial, sum_fact: enteros
se supone que la secuencia de entrada tiene al menos un número.
inicializar variables
LEER(num)
MIENTRAS(num > 0)
cant ← cant + 1
calcular factorial de num
sum_fac ← sum_fac + factorial
FIN MIENTRAS
calcular promedio de factoriales
ESCRIBIR(promedioFactorial)
Calcular factorial de num:
PARAR
factorial ← 1
inicializar variables:
HACER(num)VECES(i=num,1,-1)
cant ← 0
factorial ← factorial * i
promedioFactorial ← 0
FIN HACER
sum_fact ← 0
calcular promedio de factoriales:
promedioFactorial ← sum_fac/cant
3- Diseñar un algoritmo que encuentre el valor de las variables booleanas que
satisfagan la siguiente igualdad ¬x y = ¬x z
ALGORITMO
ENTRADA
SALIDA
: valores
: : x, y, z: booleano
x ← VERDADERO
y ← VERDADERO
z ← VERDADERO
HACER(2)VECES
HACER(2)VECES
HACER(2)VECES
SI((¬x ∧ y) = (¬x ∧ z))ENTONCES
ESCRIBIR(x,y,z)
z ← ¬z
FIN MIENTRAS
y ← ¬y
FIN MIENTRAS
x ← ¬x
FIN MIENTRAS
PARAR
Nota: El cuerpo del bucle más interno se ejecuta 2*2*2= 23 veces, que es la cantidad
de combinaciones posibles para los distintos valores que puedan tomar de las
variables booleanas x, y, z.
4- En el mes de Enero, una estación meteorológica se registran medidas de humedad
diarias al comienzo de cada día. En los días muy húmedos también es necesario
obtener los valores de temperatura cada tres horas, y calcular la temperatura
promedio de ese día. Se considera un día muy húmedo cuando la humedad relativa
supera el 60%. Como resultado se desea mostrar el día, la humedad, y temperatura
promedio de los dos días mas húmedos en caso de haberla registrado.
ALGORITMO
ENTRADA
SALIDA
VAR. AUX.
CONSTANTE
: Días húmedos y calurosos
: humedad: secuencia de números reales
temperatura: secuencia de números reales
: diaMaxA, diaMaxB: entero
humedadMaxA, humedadMaxB: real positivo
tempPromedioDiaMaxA, tempPromedioDiaMaxB: real
: tempAcumulada, tempPromedioDiaria: reales; día: entero positivo
: DIAS_DEL_MES = 31; INTERVALO=3
inicializar variables
HACER(DIAS_DEL_MES)VECES(día=1, DIAS_DEL_MES)
LEER(humedad)
SI(humedad > 60)ENTONCES
calcular temperatura promedio
registrar los dos días más húmedos
FIN MIENTRAS
escribir salida
PARAR
inicializar variables:
humedadMaxA ← -999
humedadMaxB ← -999
tempPromedioDiaMaxA ←-999
tempPromedioDiaMaxB ←-999
calcular temperatura promedio:
tempAcumulada ← 0
HACER(24/INTERVALO)VECES(hora=0,(24-INTERVALO),+INTERVALO)
LEER(temperatura)
tempAcumulada ← tempAcumulada + temperatura
FIN MIENTRAS
tempPromedioDiaria ← tempAcumulada/(hora/INTERVALO)
escribir salida:
ESCRIBIR(diaMaxA, humedadMaxA)
SI(tempPromedioDiaMaxA ≠ -999)ENTONCES
ESCRIBIR(tempPromedioDiaMaxA)
FIN SI
ESCRIBIR(diaMaxB, humedadMaxB)
SI(tempPromedioDiaMaxB ≠ -999)ENTONCES
ESCRIBIR(tempPromedioDiaMaxB)
FIN SI
registrar los dos días mas húmedos:
SI(humedad > humedadMaxA)ENTONCES
diaMaxB ← diaMaxA
humedadMaxB ← humedadMaxA
tempPromedioDiaMaxB ← tempPromedioDiaMaxA
diaMaxA ← día
humedadMaxA ← humedad
tempPromedioDiaMaxA ← tempPromedioDiaria
SINO
SI(humedad > humedadMaxB)ENTONCES
diaMaxB ← día
humedadMaxB ← humedad
tempPromedioDiaMaxB ← tempPromedioDiaria
5- Encontrar el máximo común divisor y mínimo común múltiplo de dos números
enteros positivos.
ALGORITMO
ENTRADA
SALIDA
VAR. AUX.
:
:
:
:
máximo común divisor
num1, num2: enteros positivos
mcd, mcm: números enteros positivos
a, b, aux
LEER(num1, num2)
a ← num1
b ← num2
REPETIR
aux ← num1
num1 ← RESTO(num2, num1)
num2 ← aux
HASTA QUE(num1 = 0)
actualización
Cuerpo
del bucle
condición
mcd ← num2
mcm ← (a/mcd)*b
ESCRIBIR(mcd, mcm)
PARAR
Nota: este pseudocódigo implementa el algoritmo de Euclides, que sirve para obtener
el máximo común divisor de dos números enteros positivos.
Nota: Cabe recordar que cada una de las tres formas de la estructura algorítmica
iterativa: MIENTRAS-HACER, HACER-HASTA QUE, y HACER(N)VECES, resulta
más adecuada para resolver diferentes problemas, como se mostró en los
ejemplos. Aunque éstas tres estructuras sean intercambiables, no es una buena
virtud forzar una estructura para que resuelva un problema.