02-Sistema de fuerzas e invariantes (Terna Izquierda)

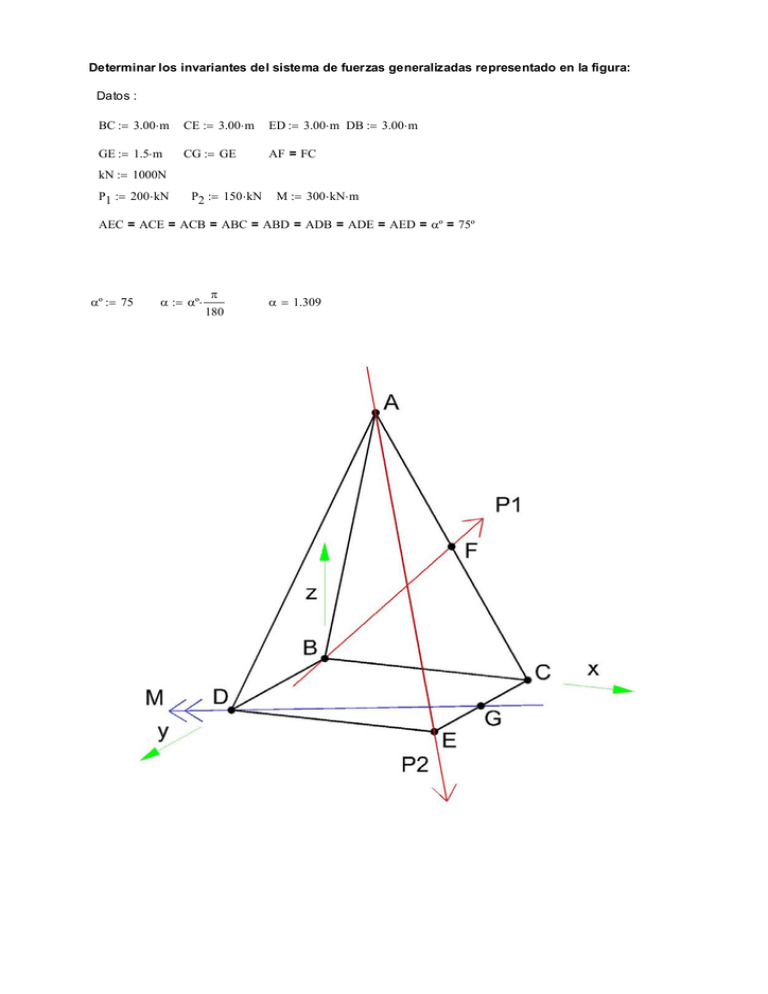
Determinar los invariantes del sistema de fuerzas generalizadas representado en la figura:
Datos :
BC := 3.00⋅ m
CE := 3.00⋅ m
ED := 3.00⋅ m DB := 3.00⋅ m
GE := 1.5⋅ m
CG := GE
AF = FC
kN := 1000N
P1 := 200 ⋅ kN
P2 := 150 ⋅ kN
M := 300 ⋅ kN⋅ m
AEC = ACE = ACB = ABC = ABD = ADB = ADE = AED = αº = 75º
αº := 75
α := αº⋅
π
180
α = 1.309
De los datos y la figura surge que:
x A := 1.5⋅ m
y A := 1.5⋅ m
Determinación de la coordenada zA.
AG := GE⋅ tan( α )
AG = 5.598 m
x F := 2.25⋅ m
2
2
AE = 5.796 m
y F := 0.75⋅ m
2
2
zA = 5.393 m
zF :=
AE :=
AG + GE
zA :=
AG − GE
⎛⎜ 1.5⋅ m ⎞⎟
A := ⎜ 1.5⋅ m ⎟
⎜ zA ⎟
⎝
⎠
⎛ 1.5 ⎞
A = ⎜ 1.5 ⎟ m
⎜
⎟
⎝ 5.393 ⎠
2
2
2
2
BF :=
x F + y F + zF
GD :=
GE + ED
2
zA
2
zF = 2.697 m
BF = 3.591 m
GD = 3.354 m
Cálculo de las componentes cartesianas de las fuerzas generalizadas.
xF
GE
P1x := P1 ⋅
P1x = 125.304 kN
P2x := P2 ⋅
BF
AE
P2x = 38.823 kN
yF
P1y := P1 ⋅
BF
P1y = 41.768 kN
P2y := P2x
P2y = 38.823 kN
zF
P1z := P1 ⋅
BF
P1z = 150.181 kN
zA
P2z := −P2 ⋅
AE
P2z = −139.591 kN
⎛ P1x ⎞
⎜ ⎟
P1 := ⎜ P1y ⎟
⎜P ⎟
⎝ 1z ⎠
⎛ 125.304 ⎞
P1 = ⎜ 41.768 ⎟ kN
⎜
⎟
⎝ 150.181 ⎠
⎛ P2x ⎞
⎜ ⎟
P2 := ⎜ P2y ⎟
⎜P ⎟
⎝ 2z ⎠
⎛ 38.823 ⎞
P2 = ⎜ 38.823 ⎟ kN
⎜
⎟
⎝ −139.591 ⎠
M x := −M ⋅
ED
GD
M x = −268.328 kN⋅ m
M y = 134.164 kN⋅ m
M z = 0 kN⋅ m
M y := M ⋅
GE
GD
⎛ Mx ⎞
⎜ ⎟
M := ⎜ M y ⎟
⎜M ⎟
⎝ z⎠
M z := M ⋅ 0
⎛ −268.328 ⎞
M = ⎜ 134.164 ⎟ kN⋅ m
⎜
⎟
⎝ 0
⎠
Reducción del sistema de fuerzas al origen B
Cálculo del vector "Resultante de Reducción":
RR := P1 + P2
⎛ 164.127 ⎞
RR = ⎜ 80.591 ⎟ kN
⎜
⎟
⎝ 10.59 ⎠
Este vector es el Invariante vectorial.
Cálculo del par de traslación del la fuerza P2 al origen B:
M P2_B := P2 × ( −A)
⎛ −418.772 ⎞
M P2_B = ⎜ 418.772 ⎟ kN⋅ m
⎜
⎟
⎝ 0
⎠
El "Momento Resultante de Reducción" del sistema de fuerzas al origen es la suma de M + M P2_B
M RR_B := M + M P2_B
⎛ −687.1 ⎞
M RR_B = ⎜ 552.936 ⎟ kN⋅ m
⎜
⎟
⎝ 0 ⎠
Finalmente, el "Invariante escalar del sistema" es la proyección (producto escalar) del vector Momento
Resultante de Reducción sobre la dirección del vector Resultante de Reducción:
RR
Ie := M RR_B ⋅
RR
Ie = −372.423 kN⋅ m
Este número es el Invariante escalar
Nota : En esta figura
pueden observarse las
dimensiones que
permiten calcular los
cosenos directores de
todos los vectores del
problema.
Ing. Pablo H. Szaingurten