Taller 2 - Inicio - Universidad de los Andes

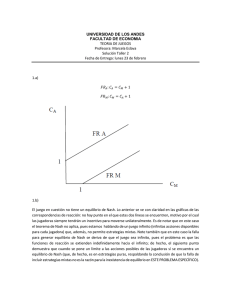
UNIVERSIDAD DE LOS ANDES FACULTAD DE ECONOMIA TEORIA DE JUEGOS Profesora: Marcela Eslava Taller 2 Para entregar miércoles 31 de agosto de 2016 al inicio de clase 1. Francia (F) y Alemania (A) deben decidir el nivel de crédito que extenderán a un tercer país, digamos Portugal. Cada uno de estos potenciales acreedores decide un monto de crédito que financiará, y
respectivamente. El total de crédito que la Unión Europea dará a Portugal estará dado por la suma de esos dos montos. Denotaremos ese nivel total de crédito como D, . Francia y Alemania toman sus decisiones de manera de tal manera que simultánea e individual, y la información sobre las funciones de utilidad de todos los jugadores es completa. Las funciones de pago son las siguientes, donde C es un monto de crédito (positivo, fijo y conocido por todos) que Portugal necesita para salir avante. (1) (2) a. Encuentre la función o correspondencia de reacción de cada uno de estos países y explique la intuición detrás de las funciones. b. Imponiendo la condición , encuentre el o los equilibrios de Nash de este juego. c. Defina el bienestar de la Unión como la suma de las utilidades de Francia y Alemania. Muestre que el nivel de deuda portuguesa que maximiza este bienestar difiere del nivel total de deuda en el Equilibrio de Nash del punto 1b. ¿Es mayor o menor? d. ¿Es el Equilibrio de Nash del punto 1b un óptimo de Pareto? Demuestre. 2. Considere el juego entre dos conductores de buseta, cada uno de los cuales decide si parar en el paradero o un poco antes. El valor del boleto de bus es 2 (en miles de pesos). El que logre parar antes que el otro se queda con ese valor. Las decisiones se toman de manera simultánea y con información completa sobre la función de utilidad del otro jugador (además de la propia). La matriz de pagos es: Conuductor 1 Conductor 2
Paradero
Antes
Paradero (1,1)
(0,2)
Antes
(1,1)
(2,0)
a. Solucione el juego por eliminación de estrategias estrictamente dominadas. Encuentre también el o los Equilibrio de Nash. Escriba ambas soluciones. ¿Coinciden? b. Considere la posibilidad de imponer una multa a los que paran antes del paradero. La multa es de valor m. ¿Cómo se modifica la matriz de pagos? ¿En qué rango debe caer el valor de m para que, en equilibrio de Nash, ambos jugadores escojan parar en el paradero? 3. Dos jugadores deben escoger, cada uno, un número entero entre 180 y 300. El objetivo de cada uno es maximizar su pago. A ambos se les entrega una cantidad, en dólares, igual al menor de los dos números que escogieron. Se transfieren 5 dólares del que escogió el mayor de esos números al que escogió el menor. SI ambos escogieron el mismo número no hay transferencia. EL juego es estático y con información completa. a. Encuentre la función o correspondencia de reacción de cada jugador. Escríbala y explíquela. b. Encuentre el o los equilibrios de Nash.