Hexaedros - geometría descriptiva

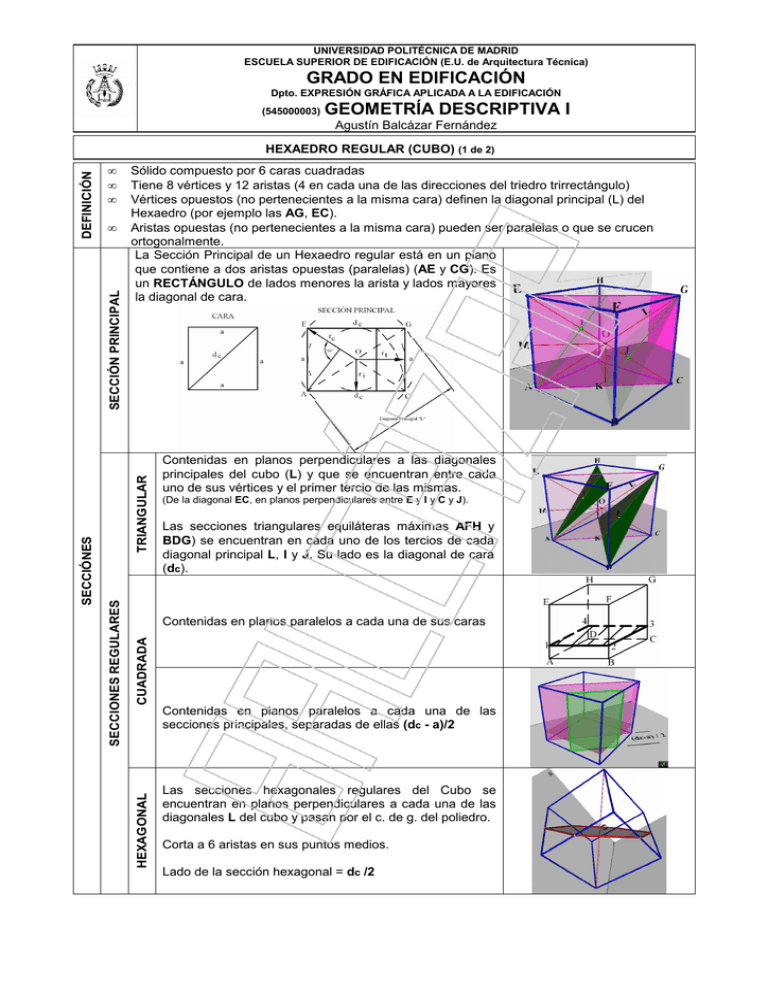
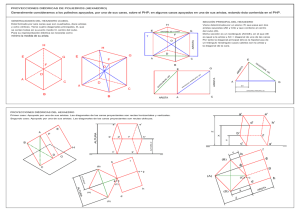
UNIVERSIDAD POLITÉCNICA DE MADRID
ESCUELA SUPERIOR DE EDIFICACIÓN (E.U. de Arquitectura Técnica)
GRADO EN EDIFICACIÓN
Dpto. EXPRESIÓN GRÁFICA APLICADA A LA EDIFICACIÓN
(545000003)
GEOMETRÍA DESCRIPTIVA I
Agustín Balcázar Fernández
•
•
•
•
TRIANGULAR
Sólido compuesto por 6 caras cuadradas
Tiene 8 vértices y 12 aristas (4 en cada una de las direcciones del triedro trirrectángulo)
Vértices opuestos (no pertenecientes a la misma cara) definen la diagonal principal (L) del
Hexaedro (por ejemplo las AG, EC).
Aristas opuestas (no pertenecientes a la misma cara) pueden ser paralelas o que se crucen
ortogonalmente.
La Sección Principal de un Hexaedro regular está en un plano
que contiene a dos aristas opuestas (paralelas) (AE y CG). Es
un RECTÁNGULO de lados menores la arista y lados mayores
la diagonal de cara.
Contenidas en planos perpendiculares a las diagonales
principales del cubo (L) y que se encuentran entre cada
uno de sus vértices y el primer tercio de las mismas.
(De la diagonal EC, en planos perpendiculares entre E y I y C y J).
Las secciones triangulares equiláteras máximas AFH y
BDG) se encuentran en cada uno de los tercios de cada
diagonal principal L, I y J. Su lado es la diagonal de cara
(dc).
CUADRADA
Contenidas en planos paralelos a cada una de sus caras
Contenidas en planos paralelos a cada una de las
secciones principales, separadas de ellas (dc - a)/2
HEXAGONAL
SECCIONES REGULARES
SECCIÓNES
SECCIÓN PRINCIPAL
DEFINICIÓN
HEXAEDRO REGULAR (CUBO) (1 de 2)
Las secciones hexagonales regulares del Cubo se
encuentran en planos perpendiculares a cada una de las
diagonales L del cubo y pasan por el c. de g. del poliedro.
Corta a 6 aristas en sus puntos medios.
Lado de la sección hexagonal = dc /2
UNIVERSIDAD POLITÉCNICA DE MADRID
ESCUELA UNIVERSITARIA DE ARQUITECTURA TÉCNICA
GRADUADO EN INGENIERÍA DE EDIFICACIÓN
Dpto. EXPRESIÓN GRÁFICA APLICADA A LA EDIFICACIÓN
(545000003)
GEOMETRÍA DESCRIPTIVA I
Agustín Balcázar Fernández
HEXAEDRO REGULAR (CUBO) (2 de 2)
EJERCICIOS
1. En el plano P se encuentra una cara.
Datos:
•
El plano P.
•
Centro de la cara K y su posición en dicho plano.
•
El valor de la Arista.
Proceso para su representación:
Dibujo de la cara con el valor de la arista dada y su sección principal, en verdadera magnitud.
Abatir el plano P.
Dibujar en el abatimiento la cara ABCD en la posición que nos digan.
Representación diédrica de dicha cara.
Por alguno de los vértices de la cara (p.e. A), dibujar una recta perpendicular al plano en que está situada.
Llevar sobre esa recta a partir del vértice elegido, y en verdadera magnitud, la arista del cubo, para
obtener el vértice E.
Trazar la cara EFGH paralela a la ABCD.
Unir todos los vértices.
Visibilidad del poliedro.
2. En el plano P se encuentra una sección principal.
Datos:
•
El plano P.
•
Centro de la sección principal (=centro del cubo) y su posición en dicho plano.
•
El valor de la diagonal principal (L).
Proceso para su representación:
1. Dibujo de la cara con un valor de la arista arbitrario y su sección principal, en verdadera magnitud.
• Por SEMEJANZA, obtener la sección principal relativa al dato dado L (y así, obtener su arista).
2. Abatir el plano P.
3. Dibujar en el abatimiento la sección principal, obtenida anteriormente, ACGF, en la posición que nos
digan.
4. Representación diédrica de dicha sección principal.
5. Por los puntos medios de los lados mayores de la sección principal (centros de caras K), dibujar una recta
perpendicular al plano en que está situada. (sabemos que hay dos secciones principales perpendiculares
entre sí en cada una de las direcciones de las aristas).
6. Llevamos sobre esa recta a partir de K, y en verdadera magnitud, la mitad de la diagonal de cara a cada
uno de los lados del plano P, para obtener los vértices B y D.
7. Por el otro punto medio (centro de cara), la paralela a BD para obtener F y H.
8. Ya tenemos todos los vértices. Unirlos.
9.
Visibilidad del mismo.
3. En el plano P se encuentra la sección triangular equilátera máxima.
Datos:
•
El plano P.
•
Centro I esa sección triangular AFH y su posición en el plano.
•
El valor de la diagonal de cara dc.
Proceso para su representación:
1. Dibujo de la cara con un valor de la arista arbitrario.
• Por SEMEJANZA, obtener la cara relativa a la diagonal de cara dada (y así su arista). Dibujar su
sección principal, para obtener L.
2. Abatir el plano P.
3. Dibujar en el abatimiento la sección triangular AFH, en la posición que nos digan.
4. Representación diédrica de dicha sección triangular.
5. Por el centro I de esa sección triangular dibujar una recta perpendicular al plano en que está situada.
Sobre esta recta se encuentra la diagonal principal del cubo L.
6. Llevamos sobre ella (en verdadera magnitud), un tercio de la diagonal de cara L, en uno de los lados del
plano P para obtener el vértice E.
7. A otro tercio de L en el otro lado del plano se encuentra la otra sección triangular máxima BDG, girada
60º.
8. A otro tercio de esta última sección triangular BDG se encuentra el último vértice del cubo C.
9. Unir los vértices del poliedro ABCDEFGH.
10. Visibilidad del mismo.
Por el centro del cubo (punto
medio de L) y perpendicular ella se encuentra la sección hexagonal regular del cubo. Corta a 6 aristas.