Árboles de Decisión Play Tennis Play Tennis (2)
Anuncio

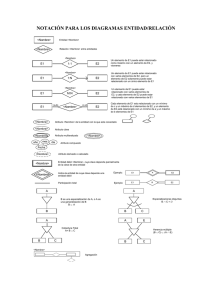
Play Tennis
• Considere el problema de aprender una
definición para el concepto "play tennis".
Esto es, si en un determinado día la gente
va a jugar al tenis o no.
Árboles de Decisión
Consideraciones sobre la
selección de atributos
• Se dispone de un conjunto de 14 ejemplos
de entrenamiento {e1, ..., e14}
• Se desea construir un árbol de decisión
(AD) para modelar el concepto
Inteligencia Artificial
Departamento de Ciencias de la Computación
Universidad Nacional del Sur - 2004
2
Play Tennis (2)
Play Tennis
Outlook
• Cada instancia se describe con los
atributos:
• outlook ∈ {overcast, sunny, rain}
• temperature ∈ {hot, mild, cool}
• humidity ∈ {high, normal}
• wind ∈ {weak, strong}
• Los ejemplos de entrenamiento son los
siguientes...
3
e1
e2
e3
e4
e5
e6
e7
e8
e9
e10
e11
e12
e13
e14
Sunny
Sunny
Overcast
Rain
Rain
Rain
Overcast
Sunny
Sunny
Rain
Sunny
Overcast
Overcast
Rain
Construcción de un AD
Hot
Hot
Hot
Mild
Cool
Cool
Cool
Mild
Cool
Mild
Mild
Mild
Hot
Mild
High
High
High
High
Normal
Normal
Normal
High
Normal
Normal
Normal
High
Normal
High
Wind
Play
Weak
Strong
Weak
Weak
Weak
Strong
Strong
Weak
Weak
Weak
Strong
Strong
Weak
Strong
No
No
Yes
Yes
Yes
Yes
Yes
No
Yes
Yes
Yes
Yes
Yes
No
4
Bondad de un atributo
• Un atributo es bueno para realizar una
partición si las particiones que obtiene son
"puras" con respecto al atributo de
clasificación
generarArbol(Meta, Ejemplos, AD):clasificanIgual(Meta, Ejemplos, AD).
generarArbol(Meta, Ejemplos, At, DT):elegir_atributo_split(Meta, E, At),
e7
e8
e9
para cada posible valor vi de At:
armar un conjunto Ei con los e ∈ E tal
que el valor de At en e es vi
para cada Ei: generarArbol(Meta, Ei, DTi)
DT ← árbol con raiz=At y subárboles DTi
Temperature Humidity
5
Bondad de un atributo (2)
Outlook
Temperature
Humidity
Wind
Play
Overcast
Cool
Normal
Strong
Yes
Sunny
Sunny
Mild
Cool
High
Normal
Weak
Weak
No
Yes
• Si el atributo de clasificación es Play, el
atributo Temperature separa mejor los
ejemplos que el atributo Outlook
6
Valores de un atributo: evaluación
Para cada posible valor vi del atributo,
considerando los ejemplos cuyo valor de atributo
es vi, evaluamos la expresión:
• Dado un conjunto de ejemplos y un
atributo, analizamos cada uno de los
posibles valores que pueda tomar
ginni(vi) =1 − [(#yes/#Ejs)2 + (#no/#Ejs)2]
(*)
donde:
• Por ejemplo, consideremos:
-#Ejs: nro Total de ejs con valor vi
-#yes: nro de ejs cuya clasificación es "yes" (true)
– conjunto de ejemplos {e1, ..., e14}
-#no: nro de ejs cuya clasificación es "no" (false)
– atributo: outlook
– valores posibles: sunny, overcast, rain
7
Estamos considerando que el atributo de clasificación (Play)
es booleano, por ello solo consideramos dos términos en la
expresión (*). Uno para #yes y otro para #no
8
Outlook ∈ {overcast, sunny, rain}
sunny
14
ejemplos
overcast
9 - 11
3 - 7 - 12
- 13
1-2-8
0.48
rain
Ginni(sunny)
= 1 - [(2/5)2 + (3/5)2]
= 0.48
4-5
6 - 10
Ginni(overcast)
= 1 - [(4/4)2 + (0/4)2]
=0
14
0
0.32
Ginni(rain)
= 1 - [(4/5)2 + (1/5)2]
= 0.32
El valor gini(vi) mide el grado de impureza del cjto
de ejemplos con valor vi con respecto al atributo en cuestión
9
Valores extremos: 0 (más puro) y 0.5 (menos puro)
Partición Outlook
• Considerando las particiones que produce
c/u de los valores del atributo se analiza la
"calidad" de la partición que provoca el
atributo
k
i =1
ni
ginni
n
i
Ginnioutlook= (5/14) 0.48 + (4/14) 0 + (5/14) 0.32
n: cantidad total de ejemplos (14)
ni: cantidad de ejemplos con valor de atributo i
Todas las particiones
10
Mejor atributo
Ginnioutlook= (5/14) 0.48 +
(4/14) 0 +
(5/14) 0.32
0.286
Ginnihumidity= (7/14) 0.489 +
(7/14) 0
Ginnitemperature= (4/14) 0.5 +
(6/14) 0.444 +
(4/14) 0.333
0.333
Seleccionamos el atributo que tiene menor valuación. En
este caso utilizamos el atributo humidity para realizar la
primera partición
0.244
humidity
Ginnihumidity= (7/14) 0.489 +
(7/14) 0
0.244
Ginniwind= (8/14) 0.375 +
(6/14) 0.444
0.404
high
normal
yes
11
1,2,3,4
8,12,14
12