BCS Databases - Bilbao Crystallographic Server

THE BILBAO CRYSTALLOGRAPHIC SERVER:
CRYSTALLOGRAPHIC DATABASES
AND COMPUTER PROGRAMS
Mois I. Aroyo, J. M. Perez-Mato and Danel Orobengoa
Universidad del Pais Vasco, Bilbao, Spain
martes 23 de junio de 2009
martes 23 de junio de 2009
Contributing authors
Universidad del Pais Vasco, Bilbao
Eli Kroumova
Svetoslav Ivantchev
Cesar Capillas
Danel Orobengoa
Gemma de la Flor
Gotzon Madariaga
J. M. Perez-Mato
Mois I. Aroyo
martes 23 de junio de 2009
Contributing authors
International Cooperation
Technische Universität, Karlsruhe, Germany
Hans Wondratschek
Universität Bonn, Germany
Rudolf Hund
Sofia University, Bulgaria
Assen Kirov
Brigham Young University, Provo, USA
Dorian Hatch
Harold Stokes
Institut Laue-Langevin, Grenoble, France
Juan Rodriguez-Carvajal
martes 23 de junio de 2009
Crystallographic databases
Group-subgroup
relations
Structural utilities
Representations of
point and space groups
Solid-state applications
martes 23 de junio de 2009
Crystallographic
Databases
International Tables for
Crystallography
martes 23 de junio de 2009
Space-group Data
International Tables for Crystallography
Volume A: Space-group
symmetry
generators
Wyckoff positions
Wyckoff sets
normalizers
Volume A1: Symmetry
Relations between space
groups
maximal subgroups of
index 2,3 and 4
series of isomorphic
subgroups
Retrieval tools
martes 23 de junio de 2009
ITA space group P4mm
No. 99
CONTINUED
Generators selected
1; t 100; t 010; t 001; 2; 3; 5
P4mm
GENPOS
Positions
Coordinates
Multiplicity,
Wyckoff letter,
Site symmetry
8
g
1
Reflection conditions
General:
(1) x y z
(5) x ȳ z
(2) x̄ ȳ z
(6) x̄ y z
(3) ȳ x z
(7) ȳ x̄ z
(4) y x̄ z
(8) y x z
no conditions
Special:
1
2
1
2
1
2
1
2
4
f
m
x
4
e
m
x0z
x̄ 0 z
4
d
m
xxz
x̄ x̄ z
2
c
2mm
1
2
0z
0
1
b
4mm
1
2
1
2
z
no extra conditions
1
a
4mm
00z
no extra conditions
z
x̄
1
2
z
xz
x̄ z
no extra conditions
0xz
0 x̄ z
no extra conditions
x̄ x z
x x̄ z
WYCKPOS
no extra conditions
z
hkl : h
k
2n
Symmetry of special projections
Along 001 p 4 m m
b b
a a
Origin at 0 0 z
Along 100 p 1 m 1
b c
a b
Origin at x 0 0
Along 110 p 1 m 1
1
a b
b
a
2
Origin at x x 0
c
Maximal non-isomorphic subgroups
[2]P4 1 1 (P4, 75)
1; 2; 3; 4
I
IIa
IIb
[2]P2 1 m (C m m 2, 35) 1; 2; 7; 8
[2]P2 m 1 (P m m 2, 25) 1; 2; 5; 6
none
[2]P42 m c(c 2c)(105); [2]P4 c c(c 2c)(103); [2]P4 2 c m(c
[2]F 4 m c(a 2a b 2b c 2c)(I 4 c m, 108); [2]F 4 m m(a
MAXSUB
2c)(101); [2]C 4 m d(a 2a b 2b)(P4 b m, 100);
2a b 2b c 2c)(I 4 m m, 107)
Maximal isomorphic subgroups of lowest index
IIc [2]P4 m m(c 2c)(99); [2]C 4 m m(a 2a b 2b)(P4 m m, 99)
Minimal non-isomorphic supergroups
I
[2]P4 m m m(123); [2]P4 n m m(129)
II
[2]I 4 m m(107)
martes 23 de junio de 2009
MINSUP
SERIES
Transformation
of the basis
martes 23 de junio de 2009
ITA-settings
symmetry data
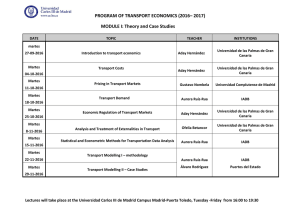
PRACTICAL EXERCISES
Bilbao Crystallographic Server
www.cryst.ehu.es
Bilbao Crystallographic Server - mirror site
http://158.227.0.68/
martes 23 de junio de 2009
MATRIX-COLUMN
PRESENTATION OF
SYMMETRY OPERATIONS
martes 23 de junio de 2009
Crystallographic symmetry operations
Symmetry operations of an object
The isometries which map the object onto itself are called symmetry operations of this
object. The symmetry of the object is the set of all its symmetry operations.
Crystallographic symmetry operations
If the object is a crystal pattern, representing a real crystal, its symmetry operations are
called crystallographic symmetry operations.
The equilateral triangle allows six symmetry
operations: rotations by 120 and 240 around its
centre, reflections through the three thick lines
intersecting the centre, and the identity operation.
martes 23 de junio de 2009
Description of isometries
coordinate system:
isometry:
martes 23 de junio de 2009
{O, a, b, c}
point X −→ point X̃
Matrix formalism
linear/matrix
part
matrix-column
pair
martes 23 de junio de 2009
translation
column part
Seitz symbol
Matrix formalism
combination of isometries:
inverse isometries:
martes 23 de junio de 2009
Matrix formalism: 4x4 matrices
augmented
matrices:
point X −→ point X̃ :
martes 23 de junio de 2009
4x4 matrices: general formulae
point X −→ point X̃ :
combination and inverse of isometries:
martes 23 de junio de 2009
EXERCISES
Problem 1.1
Construct the matrix column pair (W,w) (and the
corresponding (4x4) matrix) of the following
coordinate triplets:
(1) x,y,z
(2) -x,y+1/2,-z+1/2
(3) -x,-y,-z
(4) x,-y+1/2, z+1/2
martes 23 de junio de 2009
GEOMETRIC MEANING
OF
MATRIX-COLUMN
PAIRS (W,w)
martes 23 de junio de 2009
Crystallographic symmetry operations
characteristics:
fixed point P̃ = P
of isometries
Types of isometries preserve handedness
identity:
the whole space fixed
translation t:
no fixed point
rotation:
one line fixed
rotation axis
φ = k × 360 /N
no fixed point
screw axis
screw vector
screw rotation:
martes 23 de junio de 2009
x̃ = x + t
◦
do not
Types of isometries
preserve handedness
roto-inversion:
inversion:
reflection:
glide reflection:
martes 23 de junio de 2009
centre of roto-inversion fixed
roto-inversion axis
centre of inversion fixed
plane fixed
reflection/mirror plane
no fixed point
glide plane
glide vector
Geometric meaning of (W , w )
W information
(a) type of isometry
rotation angle
martes 23 de junio de 2009
Geometric meaning of (W , w )
W information
Texto
(b) axis or normal direction
(b1) rotations:
=
(b2) roto-inversions:
reflections:
martes 23 de junio de 2009
:
Geometric meaning of (W , w )
W information
(c) sense of rotation:
for rotations or
rotoinversions with k>2
det(Z):
x non-parallel to
martes 23 de junio de 2009
Geometric meaning of (W , w )
w -information
(A) intrinsic translation part :
(A1) screw rotations:
(A2) glide reflections:
martes 23 de junio de 2009
glide or screw
component
t/k
Geometric meaning of (W , w )
w -information
(B) location (fixed points xF ):
(B1) t/k = 0:
(B2) t/k ≠ 0:
martes 23 de junio de 2009
EXERCISES
Problem 1.1(cont.)
Construct the matrix-column pairs (W,w) (and the
corresponding (4x4) matrices) of the following
coordinate triplets:
(1) x,y,z
(2) -x,y+1/2,-z+1/2
(3) -x,-y,-z
(4) x,-y+1/2, z+1/2
Characterize geometrically these matrix-column
pairs taking into account that they refer to a
monoclinic basis with unique axis b, i.e. determine
(i) the type, (ii) glide (screw) components, (iii)
fixed points, (iv) nature and location of the
symmetry elements.
martes 23 de junio de 2009
Problem 1.1
SOLUTION
(i)
(ii)
martes 23 de junio de 2009
ITA description: under Symmetry operations
martes 23 de junio de 2009
EXERCISES
Problem 1.2
Consider the matrices
(iv) The geometrical meaning of (A, a), (B, b), (C, c) and (D, d)
martes 23 de junio de 2009
Problem 1.2
SOLUTION
martes 23 de junio de 2009
Problem 1.2
SOLUTION
martes 23 de junio de 2009
Problem 1.2
SOLUTION
martes 23 de junio de 2009
Problem 1.2
SOLUTION
The matrix-column pair (A, a): translation part
ITA description:
(A, a): screw rotation 21
screw rotation axis x,x,1/4
2(1/2,1/2,0) x,x,1/4
(B, b): rotation 3
rotation axis x,x,x
3- x,x,x
martes 23 de junio de 2009
Problem 1.2
SOLUTION
The matrix-column pair (C, c): translation part
(C, c): screw rotation 42
screw rotation axis x,0,1/2
martes 23 de junio de 2009
ITA description:
4+(1/2,0,0) x,0,1/2
Problem: Geometric
Interpretation of (W,w)
martes 23 de junio de 2009
SYMMETRY
OPERATION
Problem 1.3
1. Solve the problems 1.1 and 1.2 applying the
program SYMMETRY OPERATION
Problem 1.4
1. Characterize geometrically the matrix-column pairs
listed under General position of the space group
P4mm in ITA. Compare the results with the data
listed under Symmetry operations.
2.
Consider the diagram of the symmetry elements of
P4mm. Try to determine the matrix-column pairs of
the symmetry operations whose symmetry
elements are indicated on the unit-cell diagram.
martes 23 de junio de 2009
martes 23 de junio de 2009
GENERATION
OF
SPACE GROUPS
martes 23 de junio de 2009
Generators
Set of generators of a group is a set of spacegroup elements such that each element of the group
can be obtained as an ordered product of the
generators
G1 - identity
G2, G3, G4 - primitive translations
G5, G6 - centring translations
G7, G8, ... - generate the rest of elements
martes 23 de junio de 2009
Generation of trigonal and hexagonal
groups
1
3
32
6
622
martes 23 de junio de 2009
Generation of orthorhombic and
tetragonal groups
1
2
222
4
422
martes 23 de junio de 2009
EXERCISES
Problem 1.5
Generate the space group P4mm using the
selected generators
Compare the results of your calculation with the
coordinate triplets listed under General position
of the ITA data of P4mm
Compare the results of your calculations with the
BCS data using the retrieval tools GENPOS
(generators and general positions)
martes 23 de junio de 2009
martes 23 de junio de 2009
SITE-SYMMETRY
GENERAL POSITION
SPECIAL WYCKOFF
POSITIONS
martes 23 de junio de 2009
Calculation of the Site-symmetry groups
Group P-1
S={(W,w), (W,w)Xo = Xo}
(
0
-1
0
-1
martes 23 de junio de 2009
-1
0
)
1/2
0
1/2
=
-1/2
0
-1/2
Sf={(1,0), (-1,101)Xf = Xf}
Sf≃{1, -1}
isomorphic
EXERCISES
Problem 1.6
Consider the special Wyckoff positions of the
the space group P4mm.
Determine the site-symmetry groups of Wyckoff
positions 1a and 2b. Compare the results with the
listed ITA data
The coordinate triplets (x,1/2,z) and (1/2,x,z),
belong to Wyckoff position 4f. Compare their
site-symmetry groups.
martes 23 de junio de 2009
Space group P4mm
martes 23 de junio de 2009
EXERCISES
Problem 1.7
Texto
martes 23 de junio de 2009
martes 23 de junio de 2009
martes 23 de junio de 2009
CO-ORDINATE
TRANSFORMATIONS
IN
CRYSTALLOGRAPHY
martes 23 de junio de 2009
General affine transformation
5.1. TRANSFORMATIONS OF THE COORDINATE SYSTEM
P ! Q"1 :
a change of basis from (a, b) !to (a’
$ , b’)
!
$
a
a
# b' & ! P # b' # &!
c'
c'#
'
a shift of origin from O to O’ by a shift
vector p with
components
p1rules
andapply
p2 also
These
transformation
'#
to the
with respect to the basis vectors a' , b' , c' an
respect to a, b, c, which are written as column m
indices of a direction in direct space, [uvw], w
eneral affine transformation, consisting of a shift of origin by
by a shift vector p with components p1 and p2 and a change
! #$
! $
m a, b to a# , b# . This implies a change in the coordinates of
u
u
# #
from x, y to x , y . Change in the coordinates of the
# v# & ! Q# v &!
point X from (x, y) to (x’,y’)
w#
w
nverse matrices of P and p are needed. They are
In contrast to all quantities mentioned above,
"1
Q!P
position vector r or the coordinates of a po
martes 23 de junio de 2009
Problem: BASIS
TRANSFORMATION
5.1. TRANSFORMATIONS
OF THE COORDINATE SYSTEM
P ! Q"1 :
3-dimensional space !
$
a
# b' & !
(a, b, c), origin O: point X(x, y, z)
c'
(P,p)
'
These transformation rules appl
with respect to the basis
!
! !
! vectors
! !
(a , b , c ), origin
O’:
point
X(x
,
y
,
z
)
respect to a, b, c, which are writte
indices of a direction in direct sp
neral affine transformation, consisting of a shift of origin by
by a shift vector p with components p1 and p2 and a change
! #$
operations (W,w):
implies a change inof
thesymmetry
coordinates of
a, b to a# , b# . ThisTransformation
u
# #
om x, y to x , y .
# v# & !
#
-1
w
(W’,w’)=(P,p) (W,w)(P,p)
verse matrices of P and p are needed. They are
In contrast to all quantities ment
"1
Q!P
position vector r or the coordin
martes 23 de junio de 2009
r "xa (yb (zc"
e written in the following coordinate system consists of two parts, a linear part and a shift
his section, the 3-dimensional
relations between
thespace
primed
unprimed
of origin.
The
#3 ! and
3$ matrix
P of the linear part and the #3 ! 1$
ntities are treated.
column matrix p, containing the components of the shift vector p,
define
thetransformation)
transformation
he general
transformation
(affine
of the It is represented by the symbol
(a, b,
c), origin O:
point
X(x, y, z) uniquely.
p). a linear part and a shift
dinate system consists of two(P,parts,
rigin.
The #3
! 3$ matrix
linear
partpart
and implies
the #3 !
1$
s of direct
space
(P, pP)of the
(i) The
linear
a change
of orientation or length or
mn
p, containing
of the
shift a,
vector
es ofmatrix
a plane
(or a set ofthe components
both of the basis
vectors
b, c, p,
i.e.
ne
the transformation
by
the
symbol
! coordinates
! ! uniquely. It is represented
!
! !
t space
or(a
the
& &X(x
&
,
b
,
c
),
origin
O’:
point
,
y
,
z
)
#a
,
b
,
c
$
"
#a,
b,
c$P
p).
ciprocal
space
#
&
) The linear part implies a change of orientation or length or P11 P12 P13
es:
$
'
of the basis(i)vectors
b, c,change
i.e. of orientation or
linear a,
part:
length
" #a, b, c$% P21 P22 P23 (
of a point in direct space
& & &
P31 P32 P33
#a
, b , space
c $ " #a, b, c$P
s of reciprocal
#
&
" #P11 a ( P21 b ( P31 c,
direction in direct space
P11 P12 P13
$
'
of a shift vector from
P12 a ( P22 b ( P32 c,
" #a, b, c$% P21 P22 P23 (
&
new origin O
P13 a ( P23 b ( P33 c$"
P
P
P
31
32
33
of an inverse origin
n O & to origin O, with
P21ab pure
( P31linear
c, transformation, the shift vector p is zero and the
" #P11 a (For
(ii) origin shift bysymbol
a shift isvector
(P, o).p(p1,p2,p3):
( P32 c,
P12 a ( PThe
22 b determinant
part of a symmetry
of P, det#P$, should be positive. If det#P$ is
direct space
negative,
right-handed
coordinate
system is transformed into a
P23 b ( aP33
c$" origin O’
P13 a (
the
has
one
(or vice versa).
If det#P$
" 0, the new basis vectors
=O
p
#4 ! 1$ column O’
matrix
of +left-handed
coordinates
(p1,p
,p
)
in
2 3
aofpure
linear
transformation,
the
shift
vector
p
is
zero
and
the
are
linearly
dependent
and
do
not
form a complete coordinate
a point in direct space
the old coordinate system
system.
bol is (P, o).
In thisbechapter,
transformations
he
determinant of P, det#P$, should
positive.
If det#P$ is in three-dimensional space are
es:
martes 23 de junio de 2009
of basis from a, b to a , b . This implies a change in the coordinate
Fig. 5.1.3.1. General affine transformation,
consisting of a shift of origin
# #
. components p and p and a change
the point
x, yof
toax , py with
by a shift
vector
from
O tocomponents
OX# from
ontrast to all quantities mentioned above,
the
1
2
#
#
basisXfrom
a, b to space
a , b . This implies a change in the coordinates o
tion vector r or the coordinates of a ofpoint
in direct
the point
X from
x, y atoThe
x# , y# . X(x,y,z):
, z depend
also on the shift of
of the
the origin
in direct
space.
Transformation
coordinates
of
point
eral (affine) transformation is given by Also, the inverse matrices of P and p are needed. They are
"1
! #$
! $
Q
!
P
Also, the inverse matrices of P and p are needed. They are
x
x
" #%
" %
"1
and
y
!
Q
y
$
q
Q
!
P
with
# &
# &
"1
z#
z
q
!
"P
p!
and
!
$
Q11 x $ Q12 y $ Q13 z $ q1
"1
The
matrix
q
consists
of
the
components
q
!
"P
p! of the negative shift ve
"
%
#
# #
! # Q21 x $ Q22 y $qQwhich
23 z $ qrefer
2 &! to the coordinate system a , b , c , i.e.
The matrix q consists of the components of the negative shift vector
Q31 x $ Q32 y $qQwhich
q3 to the coordinate
# q# c# !#
33 z $ refer
$ q b#a$
q ! q a#system
, b , c , i.e.
mple
1
2
3
#
#
#
a
$
q
b
$
q
c
!
q
!
q
Thus, the transformation 1(Q, q)2 is the3 inverse
transformation
#
# #
(P,
p).
Applying
(Q,
q)
to
the
basis
vectors
a
,
b
, c and the or
thethetransformation
f no shift of origin is applied, i.e. p !Thus,
q# ! o,
position vector(Q, q) is the inverse transformation of
O , p).
theApplying
old basis(Q,
vectors
a,
b,basis
c with
origin
# O# are
# obtained.
(P,
q)
to
the
vectors
a
,
b
,
c
and
the origin
of pointspecial
X is transformed
by
cases
#
#
# For a two-dimensional transformation of a and b , s
, the old
basis
vectors a, b, c with origin O are obtained.
! $ O
!
$
elements
set as follows:
1
For a two-dimensional
of a# andQ33b# ,! some
x
x# of Q are transformation
Q#13
0. as follows: Q33 ! 1 and
# &Q31
23 y!
32 ! set
-origin
elements
of
are
b, c&PQ# y & ! %a
, b#!
, c#Q
&#
r# ! %a,shift:
! Q! Q
which transform in the same way as the b
Q13The
! Qquantities
23 !
z
z# Q31 ! Q32 ! 0.
vectors
a, b, c arewhich
calledtransform
covariantinquantities
areaswritten
as
The quantities
the sameand
way
the basis
-change of# basis :
matrices.
They
vectors
a, b,
c areare:
called covariant quantities and are written as row
n this case, r ! r , i.e. the position vector is invariant, although
Theyindices
are:
Miller
a plane (or a set of planes), (hkl), in di
he basis vectors and the components matrices.
arethe
transformed.
For a of
pure
#
hift of origin, i.e. P ! Q ! I, the transformed
position
vector
the
Miller
indices
of a rplane
(or a set of planes), (hkl), in direc
space
and
martes 23 de junio de 2009
ecomes
space and
!
=
−1
.
(5.3.13)
Transformation
of symmetry
(W,w):
This
shape of equation (5.3.10
) facilitatesoperations
the formulation
but not the actual
calculation. For the latter, the forms 5.3.11 or 5.3.12 are more appropriate.
point
point
X
!! !!!!!!!!
!
x ! !! !!! !
!! !!!!
!!
image
point
image point
(W,w )
old coordinates
old coordinates
(P,p)
(P,p)
(W ! , w ! )
!
! !!! !! !! !!!
x !! ! ! ! !!
!
X
!!!!!!!!!!!!!! !!!!!!!!!!! x̃
!!
! !! !!! !
!! !!!!
!!
!!!!!!!!!!!!!!
!!
............
.... ...
............
!!!! !!!!! !!! x̃ !
! ! ! ! !!
new coordinates
new coordinates
Fig. 5.3.3 Diagram of ‘mapping of mappings’.
Mapping of mappings
(W’,w’)=(P,p)-1(W,w)(P,p)
martes 23 de junio de 2009
Matrix formalism: 4x4 matrices
augmented matrices:
martes 23 de junio de 2009
Problem: SYMMETRY DATA
ITA SETTINGS
530 ITA settings of orthorhombic
and monoclinic groups
martes 23 de junio de 2009
SYMMETRY DATA: ITA SETTINGS
Monoclinic descriptions
abc
cb̄a
Transf.
HM
C 2/c
abc
C 12/c1
A12/n1
I 12/a1
A12/a1
C 12/n1
I 12/c1
A112/a
B 112/n
I 112/b
bac̄
B 112/b
A112/n
I 112/a
abc
B 2/b11
C 2/n11
I 2/c11
ācb
C 2/c11
B 2/n11
I 2/b11
Monoclinic axis b
Monoclinic axis c
Monoclinic axis a
Cell type 1
Cell type 2
Cell type 3
Orthorhombic descriptions
No.
33
martes 23 de junio de 2009
HM
P na21
abc
P na21
bac̄
P bn21
cab
P 21 nb
c̄ba
P 21 cn
bca
P c21 n
ac̄b
P n21 a
EXERCISES
Problem 2.1
Use the retrieval tools GENPOS (generators and general
positions), WYCKPOS (Wyckoff positions and
HKLCOND (reflection conditions) for accessing the
space-group data. Get the data on general and special
positions in different settings either by specifying
transformation matrices to new bases, or by selecting one
of the 530 settings of the monoclinic and orthorhombic
groups listed in ITA.
Consider the General position data of the space group
Im-3m (No. 229). Using the option Non-conventional setting
obtain the matrix-column pairs of the symmetry operations
with respect to a primitive basis, applying the transformation
(a’,b’,c’) = 1/2(-a+b+c,a-b+c,a+b-c)
martes 23 de junio de 2009
CRYSTAL-STRUCTURE
DESCRIPTIONS
martes 23 de junio de 2009
Inorganic Crystal Structure Database
lattice
parameters
space group
asymmetric-unit data
martes 23 de junio de 2009
EXERCISES
martes 23 de junio de 2009
Problem 2.2
EXERCISES
Problem 2.2
Structure 1:
Space group I41/amd, No. 141
origin choice 1 at 4̄m2
a=6.60 Å c=5.88 Å
u=0.20; v=0.34
martes 23 de junio de 2009
Problem 2.2
Structure 2: Space group I41/amd, No. 141
origin choice 2
at 2/m at 0,-1/4,1/8 from 4̄m2
a=6.6164 Å c=6.015 Å
Coordinate
Origin choice 1
transformation
p=0,-1/4,1/8
martes 23 de junio de 2009
Origin choice 2
Problem 2.2
Coordinate
transformation
primitive basis description
(viii) What are the lattice parameters of the primitive
unit cell
martes 23 de junio de 2009
Problem 2.2
Origin 2 description
SOLUTION
x’ = x - p
the rest of oxygen atoms
0, 0.0167, 0.198
martes 23 de junio de 2009
Problem 2.2
primitive basis
description
x’ =
martes 23 de junio de 2009
-1
P x
SOLUTION
Structure Utilities
martes 23 de junio de 2009
Problem: ALTERNATIVE
SETTINGS
SETSTRU
SETSTRU:
ITA-settings for the space group C2/c (No.15)
martes 23 de junio de 2009
Problem: STRUCTURE
TRANSTRU
TRANSFORMATIONSETSTRU:
structure
asymmetric
unit
martes 23 de junio de 2009
default
settings
Problem: UNIT CELL
TRANSFORMATION
martes 23 de junio de 2009
CELLTRAN
EXERCISES
Problem 2.2 (cont)
Repeat the calculations of Problem 2.2 applying the
corresposponding tools of the Bilbao Crystallographic
server. Compare the results.
martes 23 de junio de 2009
Problem: STRUCTURE
VISUALIZE
VISUALIZATION SETSTRU:
martes 23 de junio de 2009
Structure visualization
martes 23 de junio de 2009
Structure visualization
martes 23 de junio de 2009
Subperiodic groups:
rod and layer groups
Rod groups:
3dim groups with
1dim translations
Layer groups: 3dim groups with
2dim translations
martes 23 de junio de 2009
polymeric molecules
nanotubes
uniform magnetic field
to bulk crystals
bicrystals interfaces
domain walls
thin films
Databases for subperiodic
groups
International Tables for
Crystallography, Volume
E: Subperiodic groups
Data on maximal
subgroups
(Aroyo & Wondratschek)
generators
general postitions
Wyckoff positions
maximal subgroups of
index 2,3 and 4
series of isomorphic
subgroups
Retrieval tools
martes 23 de junio de 2009