Exposición en clase.

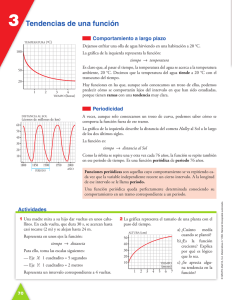
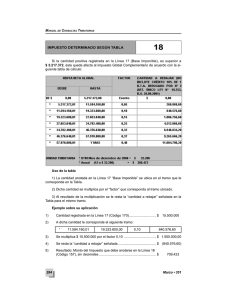
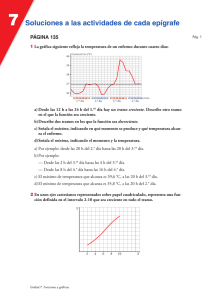
TEMA 7 FUNCIONES Y GRÁFICAS
7.1 Las funciones y sus gráficas
Actividades página 132
1.
Observando la gráfica:
Responde:
a) ¿A qué altura se encuentra el nido?
A 110 m, pues es el punto del que parte, y es donde pasa más tiempo, a esa altura.
b) ¿A qué altura estaba el águila a los cinco minutos de empezar la observación?
A 60 m, en el eje horizontal se busca el minuto cinco y sobre el, se busca la altura.
c) ¿Desde que altura otea para buscar caza?
A 50 m, pues esta es la altura que tiene antes de picar hacia el suelo.
d) ¿En qué instante caza al conejo?
A los 4 min, pues es cuando toca el suelo al ser la altura A 0 m.
e) ¿Cuánto tiempo pasa en el nido con su pareja y sus polleluelos después de cazar al
conejo?
Pasa 2 min, pues durante ese tiempo (del minuto 8 al 10 está a 110 m, que es la altura
a la que está el nido.
f) ¿A qué altura volaba la paloma que caza?
A 20 m
g) Desde que caza la paloma, ¿Cuánto tarda en subir al nido? Halla la velocidad de
subida en metros por minuto.
Tarda 2 min en subir al nido.
Al cazar a la paloma está a una altura de 20 m para luego subir hasta los 110 m.
Por lo tanto, recorre 90 m en 2 min. Entonces la velocidad es 90
45 m / min
2
Tareas 04-04-2014: 2
Actividades página 133
7.2 Variaciones de una función
Actividades página 135
1.
La gráfica siguiente refleja la temperatura de un enfermo durante cuatro días:
1
Desde las 12h a las 24 h del 1º día hay un tramo creciente. Describe otro tramo en el
que la función sea creciente.
Desde las 20h del 2º día a las 20h del 3º día.
b) Describe dos tramos en los que la función sea decreciente.
Desde el 12h del 2º día hasta las 20 h del 2º día.
Desde las 20h del 3º día hasta las 16h del 4º día.
c) Señala el máximo, indicando en qué momento se produce y que temperatura alcanza
el enfermo.
Son 39. 6º de temperatura máxima a las 20h del 3º día.
d) Señala el mínimo, indicando el momento y la temperatura.
Son 35. 8º de temperatura mínima a las 20h del 2º día.
e) Describe algún tramo en el que la función sea constante.
Desde las 4h del 4º hasta las 8h del 4º día.
En unos ejes cartesianos representados sobre papel cuadriculado, representa una función
definida en el intervalo 2, 10 (es decir, entre los valores 2 y 10, incluidos, de la variable x) que
sea creciente en todo el tramo.
Solo podemos pintar en la franja horizontal que determina el intervalo 2, 10 , de forma que
empezando a la izquierda, al ir hasta la derecha, vayamos siempre subiendo. Así, al crecer la
abscisa x también crecerá la ordenada y.
a)
2.
3.
Representa una función definida en el intervalo 0, 12 que tenga un mínimo en el punto 3, 2 y
un máximo en 7, 8 . Describe un tramo creciente y un tramo decreciente.
Una posible solución es:
2
7.3 Tendencias de una función
Página 136 Actividades
1.
Una madre mira a su hijo dar vueltas en unos caballitos. En cada vuelta, que dura 30s, se
acercan hasta casi tocarse (2m) y se alejan hasta 24m.
Representa en unos ejes la función tiempo dis tan cia
Para ello, toma las escalas siguientes:
Eje OX: un cuadradito 5s
Eje OY: un cuadradito 2 metros
Representa un intervalo correspondiente a cuatro vueltas.
Quedará de la forma siguiente:
Se trata de una función periódica de período 30s.
Otra posible solución sería:
3
2.
La gráfica representa el tamaño de una planta con el paso del tiempo.
a)
b)
c)
¿Cuánto medía cuando se plantó?
10 cm
¿Es la función creciente? Explica por qué es lógico que lo sea.
Si, pues según pasan los meses esta va ganando altura.
Es lógico pues dado que la planta se está nutriendo, ha de crecer.
¿Se aprecia alguna tendencia en la función?
Se ve que la altura tiende a estabilizarse en torno a los 55 cm de altura, dado que
llega un momento que casi no crece nada.
Observa que a la derecha del todo, la línea roja casí se vuelve horizontal.
7.4 Discontinuidades. Continuidad
Actividades página 137
1.
El precio de una fotocopia es 0. 10 euros. Representa esta función:
número de fotocopias coste
¿Se pueden unir los puntos de la gráfica?
Consideramos para empezar la siguiente tabla de valores:
x (número de fotocopias) 0 0.5
y (coste)
0
?
1
3
0.10 0.30
10 12.5 13 20 105.78
1
?
1.3
2
?
4
Quedan representados de la forma siguiente.
y
2.0
1.5
1.0
0.5
0.0
0
2.
2
4
6
8
10
12
14
16
18
20
x
No se pueden unir los puntos, pues si lo hiciesemos, tendría sentido pedir "dos fotocopias y
media".
La función es discontinua.
La gráfica de la derecha muestra las tarifas del aparcamiento de un centro comercial.
a)
b)
¿Cuánto pagamos si estamos una hora?
No se paga nada, pues las dos primeras horas es gratis.
¿Y si estamos dos horas y 30 minutos? ¿Y si estamos 8 horas?
Por dos horas y 30 minutos pagamos 2 euros.
5
c)
Por ocho horas pagamos 6 euros.
¿Es una función continua?
No es una función continua.
Su dominio es Dom f
0, 10
Su recorrido es Im f
0, 2, 4, 6
La función es discontinua en los valores de x 2, 4, 6 , pues sobre ellos es donde se
"salta" para poder seguir pintando.
7.5 Expresión analítica de una función
Actividades página 139
1.
Disponemos de una cartulina cuadrada de 8 dm de lado. Cortamos cuadraditos de lado x en las
esquinas, tal como se indica en la figura y queremos saber la superficie de la figura que queda.
Para obtener la expresión analítica de la superficie de S, resta al área del cuadrado el área de
los cuadraditos cortados.
a) ¿Cuál es la expresión de la superficie S?
Sx
8 2 4 x 2 64 16x 2
b) ¿Cuál es su dominio de definición?
Dom f
0, 4 pues para estos valores la expresión 8 2x no sale negativa.
c) ¿Y el volumen de la caja que se puede formar?
El volumen es área de la base por la altura.
Vx
8 2x 2 x
6
EJERCICIOS FINALES DEL TEMA
7