Tema: Medidas de Asociación con SPSS 1.

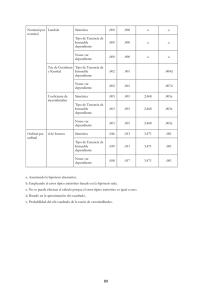
Tema: Medidas de Asociación con SPSS
1.- Introducción
Una de las tareas habituales en el análisis de encuestas es la generación y análisis de
tablas de contingencia, para las variables y categorías objetivo de la investigación. Una
tarea inicial suele consistir en la generación de múltiples tablas para el cruce de
determinadas características de interés (p.e. sexo x nivel salarial), que se suelen
acompañar en el informe de la investigación en un anexo denominado “Anexo de
Tablas”. Algunas de las tablas más “relevantes” se suelen analizar con más detalle,
haciendo uso de las llamadas Medidas de Asociación, que son estadísticos aplicados,
básicamente, a determinar si dos o más caracteres son o no dependientes entre sí (por
ejemplo si las categorías salariales tienen alguna asociación con el sexo).
El objetivo de este capítulo es describir cómo realizar un análisis de tablas de
contingencia con SPSS, y aplicar el procedimiento correspondiente a tablas de caracteres
nominales, que son los de uso común en el análisis de encuestas. No obstante, hay que
decir que SPSS puede calcular estadísticos para otros tipos de tablas para datos
ordinales, nominal por intervalo, índices de riesgo, etc., que, como decimos, no serán
objeto de esta descripción.
El procedimiento Tablas de contingencia del SPSS permite generar tablas con cualquier
número de dimensiones, aunque los estadísticos que incluye sólo son útiles para analizar
tablas bidimensionales (para más de dos criterios de clasificación se habrán de utilizar
otros procedimientos, como por ejemplo, el procedimiento Modelos log-lineales).
Si especificamos una fila, una columna y un factor de capa (variable de control), el
procedimiento Tablas de contingencia crea un panel de medidas y estadísticos asociados
para cada valor del factor de capa (o una combinación de valores para dos o más
variables de control). Por ejemplo, si sexo es un factor de capa para una tabla de casado
(sí, no) en función de vida (vida emocionante, rutinaria o aburrida), los resultados para
una tabla de doble clasificación para las mujeres se calculan de forma independiente de
los resultados de los hombres y se imprimen en paneles uno detrás del otro.
En lo que sigue utilizaremos el fichero demo.sav para ilustrar las distintas opciones del
procedimiento. Accedemos a éste en:
2.- Consideraciones sobre las variables
Para definir las categorías de cada variable, utilizaremos valores de una variable
numérica o de cadena corta (ocho caracteres o menos). Por ejemplo, para sexo,
codificaríamos los datos como 1 y 2 o como varón y mujer.
Para las tablas que consideraremos, supondremos que las variables de la tabla tienen
categorías no ordenadas (datos nominales), por tanto no nos tendremos que preocupar por
los códigos numéricos que representen las categorías. De no ser así, el procedimiento
obtendría resultados equívocos: p.e. en una variable de cadena cuyos valores sean bajo,
medio, alto, se interpreta el orden de las categorías alfabéticamente como alto, bajo,
medio, orden que no sería el correcto, de tener en cuenta el orden por la magnitud.
Como decimos, si se seleccionan una o más variables de capas, se generará una tabla de
contingencia por cada categoría de cada variable de capas (variable de control). Por
ejemplo, si emplea una variable de fila, una variable de columna y una variable de capas
con dos categorías, obtendrá una tabla de doble clasificación por cada categoría de la
variable de capas.
Para crear otra capa de variables de control, pulsaremos en Siguiente. Se crean subtablas
para cada combinación de categorías para cada variable de la 1ª capa con cada variable de
la 2ª capa, y así sucesivamente. Si se solicitan estadísticos y medidas de asociación, se
aplicarán sólo a las tablas de doble clasificación. Veamos la tabla creada con el cuadro de
diálogo anterior:
Tabla de contingencia Estado civil * Categoría de ingresos en miles * Género
Recuento
Género
Hombre
Mujer
Estado
civil
Soltero
Casado
Total
Estado
civil
Soltero
Casado
Total
Categoría de ingresos en miles
Menos de 25$ 25$ - 49$
50$ - 74$
323
653
275
288
527
273
611
1180
548
255
575
277
308
633
295
563
1208
572
75$ o +
440
442
882
426
410
836
Total
1691
1530
3221
1533
1646
3179
Podemos observar que se crea una tabla de doble entrada cuyas columnas son las
categorías de ingresos y cuyas filas están formadas por el cruce de las variables estado
civil y sexo, que es la variable incluida en capa. No obstante, seguidamente se muestra
que los estadísticos de asociación que proporciona el programa son los correspondientes a
cada una de las tablas (Hombre – Mujer) de las categorías de la variable capa:
Pruebas de chi-cuadrado
Género
Hombre
Mujer
3
3
Sig. asintótica
(bilateral)
,059
,059
3,939
1
,047
3221
4,636b
4,638
3
3
,200
,200
4,479
1
,034
Valor
7,442a
7,447
Chi-cuadrado de Pearson
Razón de verosimilitud
Asociación lineal por
lineal
N de casos válidos
Chi-cuadrado de Pearson
Razón de verosimilitud
Asociación lineal por
lineal
N de casos válidos
gl
3179
a. 0 casillas (,0%) tienen una frecuencia esperada inferior a 5. La frecuencia
mínima esperada es 260,30.
b. 0 casillas (,0%) tienen una frecuencia esperada inferior a 5. La frecuencia
mínima esperada es 271,49.
3.- Estadísticos
Las medidas de asociación que vamos a describir están basados en el estadístico Chicuadrado. Este estadístico, propuesto por Fisher, es una función de las diferencias entre
las frecuencias observadas y las esperadas si los caracteres fuesen independientes. Se
calcula como sigue:
X = ∑∑
2
i
j
(oij − eij ) 2
eij
, con eij =
Ri xC j
n
donde oij son las frecuencias observadas, eij las frecuencias esperadas, Ri el total de la
fila i, C j el total de la columna j, y n el número total de casos. Para que las
probabilidades de la distribución del estadístico constituyan una buena aproximación a la
distribución Chi-cuadrado se deben cumplir algunas condiciones; entre ellas, que las
frecuencias esperadas no sean demasiado pequeñas. Suele asumirse que, si existen
frecuencias esperadas menores que 5, éstas no deben superar el20 por ciento del total de
frecuencias esperadas, de no ser así los resultados se deben interpretar con cautela. La
salida del SPSS muestra un mensaje indicando el valor de la frecuencia esperada más
pequeña; si existe alguna casilla con frecuencia esperada menor que 5, la salida también
muestra el porcentaje que éstas representan sobre el total de casillas de la tabla.
Por otra parte, puesto que el estadístico vale 0 en el caso de independencia, es claro que
cuanto mayor sea éste, mayor será la asociación entre los caracteres. Dicha asociación
será significativa cuando el p-valor asociado al estadístico sea inferior al nivel de
significación propuesto (usualmente 0.05). Para el caso de la tabla generada
anteriormente, no hay evidencia para rechazar la independencia entre los caracteres, tanto
para hombres como para mujeres.
El estadístico chi-cuadrado de Pearson permite contrastar la hipótesis de independencia
en una tabla de contingencia, pero no nos dice nada sobre la intensidad de la asociación
entre las variables estudiadas. Esto es debido a que su valor depende, no sólo del grado en
que los datos se ajustan al modelo de independencia, sino del número de casos de que
consta la muestra. Con tamaños muestrales muy grandes, diferencias relativamente
pequeñas entre las frecuencias observadas y las esperadas pueden dar lugar a valores chicuadrado demasiado altos. Por esta razón, para estudiar el grado de relación existente
entre dos variables se utilizan medidas de asociación que intentan cuantificar ese grado
de relación eliminando el efecto del tamaño muestral.
Con este objetivo, el procedimiento proporciona además los siguientes estadísticos:
•
Chi-cuadrado de la razón de verosimilitud (Fisher, 1924; Neyman y Pearson,
1928), se obtiene calculando el valor:
⎛ oij
Razón = 2∑∑ oij log⎜
⎜e
i
j
⎝ ij
⎞
⎟
⎟
⎠
Se trata de un estadístico asintóticamente equivalente al Chi-cuadrado (se
distribuye e interpreta igual) y es muy utilizado para estudiar la relación entre
variables categóricas, particularmente en el contexto de los modelos log-lineales.
•
Estadísticos para tablas 2x2:
o Chi-cuadrado con corrección de Yates: el estadístico se calcula restando
0,5 puntos al valor absoluto de las diferencias del estadístico Chi-cuadrado
(antes de elevarlas al cuadrado).
X corr = ∑∑
2
i
j
(o
ij
− eij − 0.5
)
2
eij
Algunos autores sugieren que, con muestras pequeñas, esta corrección
permite que e] estadístico X2 se ajuste mejor a las probabilidades de la
distribución Chi-cuadrado, pero no existe un consenso generalizado sobre
la utilización de esta corrección.
o Prueba exacta de Fisher (1935) ofrece, basándose en la distribución
hipergeométrica y en la hipótesis de independencia, la probabilidad exacta
de obtener las frecuencias de hecho obtenidas o cualquier otra
combinación más alejada de la hipótesis de independencia.
•
Coeficiente de contingencia. Medida de asociación basada en chi-cuadrado. El
valor siempre está comprendido entre 0 y 1. El valor 0 indica que no hay
asociación entre la fila y la columna y los valores cercanos a 1 indican que hay
gran relación entre las variables. No obstante, el valor máximo posible depende
del número de filas y columnas de la tabla:
C=
•
Phi y V de Cramer. Phi es una medida de asociación basada en chi-cuadrado que
conlleva dividir el estadístico chi-cuadrado por el tamaño muestral y calcular la
raíz cuadrada del resultado. V de Cramer es una medida de asociación basada en
chi-cuadrado (k es el menor del número de filas o columnas).
φ=
•
•
X2
X2 +n
X2
n
V =
X2
n(k − 1)
Lambda. Medida de asociación que refleja la reducción proporcional en el error
cuando se utilizan los valores de la variable independiente para pronosticar los
valores de la variable dependiente. Un valor igual a 1 significa que la variable
independiente pronostica perfectamente la variable dependiente. Un valor igual a
0 significa que la variable independiente no ayuda en absoluto a pronosticar la
variable dependiente.
Coeficiente de incertidumbre. Medida de asociación que indica la reducción
proporcional del error cuando los valores de una variable se emplean para
pronosticar los valores de la otra variable. Por ejemplo, un valor de 0,83 indica
que el conocimiento de una variable reduce en un 83% el error al pronosticar los
valores de la otra variable. SPSS calcula tanto la versión simétrica como la
asimétrica del coeficiente de incertidumbre.
Siguiendo con nuestro ejemplo, los estadísticos que obtendremos para las tablas
propuestas son:
Medidas simétricas
Género
Hombre
Mujer
Nominal por
nominal
N de casos válidos
Nominal por
nominal
Phi
V de Cramer
Coeficiente de
contingencia
Phi
V de Cramer
Coeficiente de
contingencia
N de casos válidos
Valor
,048
,048
Sig.
aproximada
,059
,059
,048
,059
3221
,038
,038
,200
,200
,038
,200
3179
a. Asumiendo la hipótesis alternativa.
b. Empleando el error típico asintótico basado en la hipótesis nula.
Medidas direccionales
Género
Hombre
Nominal
por nominal
Lambda
Tau de Goodman
y Kruskal
Coeficiente de
incertidumbre
Mujer
Nominal
por nominal
Lambda
Tau de Goodman
y Kruskal
Coeficiente de
incertidumbre
Simétrica
Estado civil dependiente
Categoría de ingresos
en miles dependiente
Estado civil dependiente
Categoría de ingresos
en miles dependiente
Simétrica
Estado civil dependiente
Categoría de ingresos
en miles dependiente
Simétrica
Estado civil dependiente
Categoría de ingresos
en miles dependiente
Estado civil dependiente
Categoría de ingresos
en miles dependiente
Simétrica
Estado civil dependiente
Categoría de ingresos
en miles dependiente
Valor
,001
,001
Error típ.
a
asint.
,008
,019
T aproximada
,067
,067
,000
,000
.
,002
,002
,059d
,001
,001
,025
,001
,002
,001
,001
1,365
1,365
,059e
,059e
,001
,001
1,365
,059
,005
,010
,008
,019
,553
,553
,580
,580
,000
,000
.
,001
,001
,201d
,000
,000
,216
,001
,001
,001
,001
1,077
1,077
,200e
,200e
,001
,001
1,077
,200
b
c
c
Sig.
aproximada
,946
,946
.
.
c
d
e
c
d
e
a. Asumiendo la hipótesis alternativa.
b. Empleando el error típico asintótico basado en la hipótesis nula.
c. No se puede efectuar el cálculo porque el error típico asintótico es igual a cero.
d. Basado en la aproximación chi-cuadrado.
e. Probabilidad del chi-cuadrado de la razón de verosimilitud.
4.- Opciones en las casillas y gráficos
Con objeto de ayudar a interpretar las tramas en los datos que contribuyen a una prueba
de Chi-cuadrado significativa, el procedimiento Tablas de contingencia muestra las
frecuencias esperadas y tres tipos de residuos (desviaciones) que miden la diferencia
entre las frecuencias observadas y las esperadas. Cada casilla de la tabla puede contener
cualquier combinación de recuentos, porcentajes y residuos seleccionados. El cuadro de
diálogo es:
Las opciones son:
•
•
•
Frecuencias: El número de casos realmente observados y el número de casos
esperados si las variables de fila y columna son independientes entre sí.
Porcentajes: Los porcentajes se pueden sumar a través de las filas o a lo largo de
las columnas. También se encuentran disponibles los porcentajes del número total
de casos representados en la tabla (una capa).
Residuos.: Los residuos brutos no tipificados presentan la diferencia entre los
valores observados y los esperados. También se encuentran disponibles los
residuos tipificados y tipificados corregidos.
o No tipificados. Diferencia entre un valor observado y el valor
pronosticado. El valor pronosticado es el número de casos que se
esperarían en la casilla si no hubiera relación entre las dos variables. Un
residuo positivo indica que hay más casos en la casilla de los que habría en
ella si las variables de fila y columna fueran independientes.
o Tipificados. Es el residuo dividido por una estimación de su desviación
típica. Los residuos tipificados, que son conocidos también como los
residuos de Pearson o residuos estandarizados, tienen una media de 0 y
una desviación típica de 1.
o Tipificados corregidos. El residuo de una casilla (valor observado menos
valor pronosticado) dividido por una estimación de su error típico. El
residuo tipificado resultante viene expresado en unidades de desviación
típica, por encima o por debajo de la media.
•
Ponderaciones no enteras. Los recuentos de las casillas suelen ser valores enteros,
ya que representan el número de casos de cada casilla. Sin embargo, si el archivo
de datos está ponderado en un momento determinado por una variable de
ponderación con valores fraccionarios (por ejemplo, 1.25), los recuentos de las
casillas pueden que también sean valores fraccionarios. Podemos truncar o
redondear estos valores antes o después de calcular los recuentos de las casillas o
bien utilizar recuentos de casillas fraccionarios en la presentación de las tablas y
los cálculos de los estadísticos.
El procedimiento muestra los gráficos de barras agrupadas por grupos de casos. Hay una
agrupación de barras por cada valor de la variable especificada en el cuadro Filas. La
variable que define las barras dentro de cada agrupación es la variable especificada en el
cuadro Columnas. Por cada valor de esta variable hay un conjunto de barras de distinto
color o trama. Si especifica más de una variable en Columnas o en Filas, se generará un
gráfico de barras agrupadas por cada combinación de dos variables.
En nuestro ejemplo, los gráficos asociados son:
Género=Hombre
Género=Mujer
Categoría de
ingresos en miles
700
Categoría de
ingresos en miles
700
Menos de 25$
Menos de 25$
25$ - 49$
600
25$ - 49$
600
50$ - 74$
50$ - 74$
75$ o +
75$ o +
500
Recuento
Recuento
500
400
300
400
300
200
200
100
100
0
0
Soltero
Casado
Estado civil
Soltero
Casado
Estado civil