1. Con cuantos colores al menos se puede colorear cualquier mapa

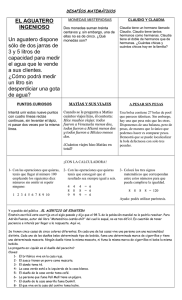
1. Con cuantos colores al menos se puede colorear cualquier mapa de tal forma que regiones vecinas(línea
fronteriza y no únicamente un punto) posean diferentes colores. Pruebe el numero dado con estos dos
mapas.
2. Los vecinos de las casas tienen todos el derecho de utilizar los tres pozos. Como no se llevan bien en
absoluto, no quieren cruzarse jamás. ¿Es posible trazar los nueve caminos que juntan las tres casas con los
tres pozos sin que haya cruces?
3. Disponemos de dos relojes de arena que permiten medir respectivamente 3 minutos y 5 minutos. Estos
relojes no disponen de barras intermedias de medida, es decir, que solamente pueden medir el tiempo que
transcurre entre la caída del primer grano de arena y la del último. Usando los relojes queremos medir
exactamente cuatro minutos. ¿Cómo lo podemos hacer?
4. ¿Cuántas veces le puedes quitar 6 a 36?
5. La policía arresta a cuatro hombres, uno de los cuales ha cometido un robo, los
mismos hacen las siguientes declaraciones:
Alberto: "Bernardo es culpable".
Bernardo: "Daniel es culpable".
Carlos: "Yo no soy culpable".
Daniel: "Bernardo miente cuando afirma que soy culpable".
Si se sabe que una sola de estas declaraciones es verdadera, ¿quien es el culpable del robo?
6. Tres amigos van a tomar café. Piden la cuenta y el camarero les dice que son 25 pesetas por los tres cafés.
Cada uno pone 10 pesetas, en total 30. Con las 5 que sobran, se queda cada uno 1 peseta, y las otras 2
para el bote del bar. Es decir, cada uno paga 9 pesetas, que por los tres serían 27, más las 2 de la propina,
29. ¿Donde está la peseta que falta
7. ¿Puedes mover sólo dos líneas(cortas) para que aparezcan dos cuadrados?
8. Tenemos 5 casas de cinco colores diferentes y en cada una de ellas vive una persona de una
nacionalidad diferente. Cada uno de los dueños bebe una bebida diferente, fuma una marca de
cigarrillos diferente y tiene una mascota diferente.
Tenemos las siguientes claves:
• El británico vive en la casa roja.
• El sueco tiene un perro.
• El danés toma té.
• La casa verde esta a la izquierda de la blanca.
• El dueño de la casa verde toma café.
• La persona que fuma Pall Mall tiene un pájaro.
• El dueño de la casa amarilla fuma Dunhill.
• El que vive en la casa del centro toma leche.
• El noruego vive en la primera casa.
• La persona que fuma Brends vive junto a la que tiene un gato.
• La persona que tiene un caballo vive junto a la que fuma Dunhill.
• El que fuma Bluemasters bebe cerveza.
• El alemán fuma prince.
• El noruego vive junto a la casa azul.
• El que fuma Brends tiene un vecino que toma agua.
Y por ultimo la pregunta:
¿Quién es el dueño del pececito?
9. La señora Pita, una gran fumadora durante muchos años, finalmente decidió dejar de fumar.
"Acabaré los veintisiete cigarrillos que me quedan", se dijo, «y jamás volveré a fumar".
La costumbre de la señora Pita era fumar exactamente dos tercios de cada cigarrillo. No
tardó mucho en descubrir que con la ayuda de una cinta engomada podía pegar tres colillas y
hacer otro cigarrillo. Con 27 cigarrillos, ¿cuántos cigarrillos puede fumar antes de abandonar el
tabaco para siempre?
10. ¿Cuántos cuadrados distintos puedees contar en el dibujo del joven hindú con turbante?
11. Coloque los números (1-9) de tal forma que todos los números en cualquier dirección siempre
suman 15.
12. 6. ¿Puedes trazar dos líneas rectas, sin levantar el lápiz del papel, que pasen por las seis pelotas
que aparecen en la ilustración?
13. Resuelve el siguiente cuadro de sudoku. Recuerde que los números son del 1- al 9 y no se deben
repetir en ninguna dirección.
14. Un caminante que llega a una posada no tiene dinero en efectivo pero sí una cadena de oro de 7
eslabones que ofrece como pago al posadero. Como no se conocen de nada, y para evitar
desconfianzas, acuerdan que el caminante irá pagando un eslabón cada día. ¿Cuál es el mínimo
número de eslabones que debe abrir el caminante para poder realizar los pagos de la forma
acordada?. Lo importante no es que el caminante le pague al posadero un eslabón cada día, sino
que el posadero tenga siempre tantos eslabones como días lleva alojado el caminante en la
posada.
15. Tenemos cuatro cubos, pintados con cuatro colores distintos y de forma que en cada uno de ellos
no aparezca un color más de dos veces. La distribución de los colores viene indicada en las
siguientes imagenes.
Coloque los cubos de tal forma que los cuatros cubos …
En fila de modo que en los cuatro lados de la fila estén los cuatro colores.
En fila de modo que en cada lado de la fila esté uno de los cuatro colores.
Formen un ortoedro de 2x2x1 de manera que las caras 2x2 tengan cada una un color. Y las cuatro
caras 2x1 sean, cada una, de un color distinto, sin que se repitan.
Formen un podium de manera que los planos de cada dirección del espacio tengan un solo color.
Formen una “L” de manera que los planos de cada dirección del espacio tengan un solo color.
Formen una “doble escalera” de manera que los planos de cada dirección del espacio (en esta
figura no se tiene en cuenta el plano oculto por la base) tengan un solo color.