Cuaderno de evidencias de Física II Preparatoria No. 22 VECTORES

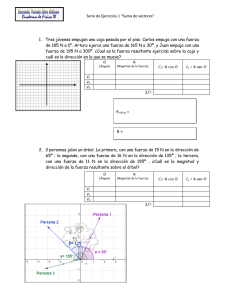
Cuaderno de evidencias de Física
II
Preparatoria No. 22
VECTORES
EL ALUMNO: Aprende y aplica el concepto de vector en su medio social donde convive.
Cuaderno de evidencias de Física II
Preparatoria No. 22
I. VECTORES
EXAMEN DIAGNÓSTICO
DADOS TUS CONOCIMIENTO PREVIOS DE FÍSICA CONTESTA:
1.
¿Qué es una cantidad escalar?
__________________________________________________________________________________________________
__________________________________________________________________________________________________
2.
¿Qué es una cantidad vectorial?
__________________________________________________________________________________________________
__________________________________________________________________________________________________
3.
Escribe 2 ejemplos de cantidades escalares
__________________________________________________________________________________________________
__________________________________________________________________________________________________
4.
Escribe 2 ejemplos de cantidades vectoriales
__________________________________________________________________________________________________
__________________________________________________________________________________________________
UTILIZANDO TU LIBRO DE TEXTO Y EL APÉNDICE DE ÉSTA UNIDAD DEFINE CADA UNO DE LOS CONCEPTOS
1. Cantidad física:
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
2. Cantidad escalar y 3 ejemplos de ellos.
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
3. Cantidad vectorial y 3 ejemplos de ellos.
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
4. ¿Cuáles son las características de un vector?
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
Ing. Jaime Lomelí Cervantes
Página 1
Cuaderno de evidencias de Física II
Preparatoria No. 22
5. Métodos Gráficos
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
5.1. Del triángulo rectángulo
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
5.2. Del triángulo oblicuángulo
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
5.3. Del paralelogramo
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
5.4. Del polígono
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
6. Métodos analíticos
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
6.1. Del triángulo rectángulo
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
6.2. De las componentes
__________________________________________________________________________________________________
__________________________________________________________________________________________________
__________________________________________________________________________________________________
7. Tomando como punto de referencia la Preparatoria No.22, ¿en qué dirección quedan ubicados los siguientes
lugares?
A) El Cerro de la Silla_____________________ B) El Aeropuerto Mariano Escobedo_______________________
C) El Cerro del Topo Chico __________________ D) Ciudad Universitaria_________________________________
E) El Auditorio Banamex(Parque Fundidora)___________________F) Cerro de Chipinque______________________
G) La cabecera municipal de Cd. Guadalupe_________________________________
Ing. Jaime Lomelí Cervantes
Página 2
Cuaderno de evidencias de Física II
Preparatoria No. 22
MÉTODO GRÁFICO
RESUELVE CADA PROBLEMA DE VECTORES
15
10
Utilizando los cuadros cartesianos mostrados a continuación dibuja
y encuentra el vector resultante en los siguientes problemas:
1. La suma de los vectores ⃗⃗
⃗⃗
en el eje x negativo.
en el eje x positivo y
2. La suma de los vectores ⃗⃗
⃗⃗
en el eje y negativo.
en el eje y positivo y
5
0
-15
-10
-5
0
5
10
15
0
5
10
15
0
5
10
15
-5
-10
-15
3. Un auto se desplaza 15km al norte y luego 22km al sur.
4. Una persona se mueve 14km al este y luego 29km al oeste.
15
10
5
0
-15
-10
-5
-5
-10
-15
15
5. Se suman un vector fuerza de 6N a 0° y luego otro de 8N a
180°.
6. Se suman un vector velocidad de 13 km/h a 90 ° y 20 km/h
a 270 °.
10
5
0
-15
-10
-5
-5
-10
-15
Ing. Jaime Lomelí Cervantes
Página 3
Cuaderno de evidencias de Física II
Preparatoria No. 22
15
7. La suma de los vectores ⃗
en
⃗⃗
el eje x positivo,
hacia el eje
y negativo,
en el eje x
⃗⃗
negativo y
hacia el eje y
positivo.
10
5
0
-15
-10
-5
0
5
10
15
-5
-10
-15
8. Dos fuerzas de 600N y 750N, respectivamente se utilizan para arrastrar un carro fuera de una zanja en la cual se
ha hundido Si el ángulo entre las dos fuerzas es de 50 , hallar la magnitud y la dirección de la fuerza resultante.
15
10
5
0
-15
-10
-5
0
5
10
15
-5
-10
-15
Ing. Jaime Lomelí Cervantes
Página 4
Cuaderno de evidencias de Física II
Preparatoria No. 22
UTILIZA HOJAS DE PAPEL MILIMÉTRICO, REGLA Y TRANSPORTADOR PARA GRAFICAR LOS SIGUIENTES
PROBLEMAS ACERCA DE VECTORES. EL RESULTADO DE TU TRABAJO ENTRÉGALO A TU MAESTRO.
1)
Una persona camina 4 km hacia el este, luego 3 km hacia el sur. Calcula la magnitud y la dirección del desplazamiento
resultante.
2)
Una lancha de motor se desplaza 300km al oeste, 200km al norte, 350km al noreste y 150km al sur, calcula el desplazamiento
resultante. (300km en dirección noroeste que forma un ángulo de 80.5° medido a partir del oeste).
3)
Determina la magnitud y la dirección de la fuerza resultante de la fuerza resultante del siguiente sistema de fuerzas: F 1=60N a
40°; F2=20N a 75°.
4)
Un automóvil Volvo recorre 80Km al oeste y luego 30km hacia al suroeste. Determina la magnitud la dirección del
desplazamiento resultante del automóvil desde el punto de partida.
5)
Determina la fuerza resultante de:F1=90N a 1=135°, F2 =80N a 2 =275° y F3 =48N a 3 =190°
MÉTODO ANALÍTICO
DETERMINAR LA RESULTANTE DE LOS SIGUIENTES VECTORES:
1.- | ̅ |
4
|̅|
3
|̅|
2.- | ̅ |
7
|̅|
8
|̅|
|̅|
|̅|
𝐴
𝐵
𝐶
̅
𝐷
Ing. Jaime Lomelí Cervantes
Página 5
Cuaderno de evidencias de Física II
Preparatoria No. 22
SUPONIENDO QUE LA MAGNITUD DE VÉRTICE A VÉRTICE DE CADA CUADRITO ES LA UNIDAD Y EL ÁNGULO DE
INCLINACIÓN DE TODOS LOS VECTORES ES DE 45° CON RESPECTO A LA HORIZONTAL Y A LA VERTICAL,
CALCULA LAS SIGUIENTES SUMAS DE VECTORES:
1.- A+B=
2.- A+ (-B)=
3.- B+(-A)=
4.- C+D=
5.- C+(-D)=
6.- D+(-C)=
7.- E+F=
8.- E+(-F)=
9.- F+(-E)=
10.- G+H=
11.- G+(-H)=
12.- H+(-G)=
𝐴
⃗
𝐵
-6
-5
-4
-3
-2
𝐸⃗
𝐹
7
6
5
4
3
2
1
0
-1 -1 0
-2
-3
-4
-5
-6
-7
-8
⃗
𝐷
𝐶
1
2
3
4
5
6
𝐺
⃗
𝐻
CONSIDERANDO LA SIGUIENTE GRÁFICA DETERMINA LO SIGUIENTE:
1. ∑
2. ∑
-6
-5
-4
-3
-2
8
7
6
5
4
3
2
1
0
-1-1 0
-2
-3
-4
-5
-6
-7
-8
Ing. Jaime Lomelí Cervantes
1
2
3
4
5
6
7
8
3.
=
9
Página 6
Cuaderno de evidencias de Física II
Preparatoria No. 22
RESUELVE CADA PROBLEMA DE VECTORES USANDO EL MÉTODO ANALÍTICO COMO EL DEL TRIÁNGULO O EL
DE LAS COMPONENTES:
1)
Calcula la componente vertical del vector de 1220N a un
ángulo de 30°.
2)
Vy=610N
Vx=2681.15N
3)
Calcula la componente vertical del vector de 200N a un
ángulo de 20°.
4)
Vy=68.4N
Calcula la componente horizontal del vector de 3500N a un
ángulo de 40°.
Calcula la componente horizontal del vector de 2300N a un
ángulo de 26°.
Vx=2067.22N
5)
Calcula componente vertical, si la componente horizontal es 6)
Calcula componente horizontal, si la componente vertical es
de 800km y el vector es de 1000km.
de 7500m/s2 y el vector es de 12500 m/s2.
Vx=10000
m/s2
Vy=600km
7)
Una barca se ha desplazado 150km a 0° y luego cambia a
135km a 180°. Calcula el desplazamiento resultante.
15km a 0°
8)
Un avión se ha desplazado 1600km a 90° y luego cambia a
1850km a 270°. Calcula el desplazamiento resultante.
250km a 270°
9)
Encuentra la magnitud y la dirección de la fuerza resultante 10) Un hombre camina 5 km hacia el este y luego 10 km hacia
producida por una fuerza vertical hacia arriba de 40 N y otra
el norte. Encuentra la magnitud y la dirección del
fuerza horizontal hacia la derecha de 30 N.
desplazamiento desde el punto de partida.
DR =11.2km, ΘR = 63.43o al norte del este (noreste)
FR = 50 N ΘR= 53.13
Ing. Jaime Lomelí Cervantes
Página 7
Cuaderno de evidencias de Física II
Preparatoria No. 22
11)
Un avión vuela de la ciudad A a la ciudad B, 2300km al sur, 12)
luego cambia de dirección 3000km al oeste, ¿cuál debería
ser la ruta mas corta para trasladarse de A a B?
3780.21km 37.47° al sur del oeste.
Un murciélago desea atrapar un insecto que está
justamente debajo de él 20m, pero con su radar de ondas
sonoras detecta que se desplaza horizontalmente y en
pocos segundos se desplazará 25m después de haberlo
detectado. ¿Qué trayectoria en línea recta debe seguir el
murciélago para atrapar al insecto?
32.01m a un ángulo de depresión de 38.66°
13)
Un río llamado Río Bravo, tiene su caudal de oeste a este
14) Una plaza tiene 120m de largo y 50m de ancho. Una
con una velocidad de 3m/s y una lancha lo comienza a
persona va a ir de una esquina a la opuesta.
atravesar con una velocidad de sur a norte de 4m/s. ¿Cuál a) ¿Cuántos metros habrá de caminar si cruza la plaza?. 130m
es la trayectoria final de la lancha? 5m/s a 53.13° al norte b) ¿Cuántos metros caminará si se va por la banqueta que
del este.
conduce por cada lado de la plaza? 170m
15)
Un periodista ganó el premio Pulitzer, por tomar la
fotografía de una niña en Sudán, a punto de morir a causa
del hambre y un buitre asechándola. El periodista, la niña y
el buitre con su ubicación formaban un triángulo rectángulo
y la niña estaba en el ángulo recto; el buitre y el periodista
estaban en los otros dos vértices a 25m entre ellos y con el
buitre a 20m de la niña, ¿a cuántos metros de distancia
estuvo el periodista de salvar la vida de la niña? El
periodista nunca se acercó a la niña para ayudarla.
15m
Ing. Jaime Lomelí Cervantes
16)
El campo de fútbol que usan en Brasil mide 120 m de
largo y 90 m de ancho y tiene forma rectangular.
¿Cuántos metros debe desplazarse un jugador si cruza el campo
de una esquina a la esquina opuesta? 150m
¿Cuántos metros caminará un jugador en caminar de una esquina
a la opuesta sin cruzar el campo?
210m
Página 8
Cuaderno de evidencias de Física II
17)
Preparatoria No. 22
Una persona camina 4 km hacia el este, luego 3 km hacia
el sur. Calcula la magnitud y la dirección del
desplazamiento resultante.
DR=5km, ΘR = 36.87 al sur del este ( sureste)
18)
19)
20)
¿Qué fuerza se debe sumar a otra de 500N que está en el
eje horizontal positivo para que la fuerza resultante sea de
850N a 25° con la horizontal?
Nota: este problema requiere destreza matemática
450N a 53°
Dos fuerzas de 600N y 750N, respectivamente se utilizan
para arrastrar un carro fuera de una zanja en la cual se ha
hundido Si el ángulo entre las dos fuerzas es de 50 , hallar
la magnitud y la dirección de la fuerza resultante.
FR=1225.16N, ΘR=28 a partir de la Fuerza de 600 N
La componente horizontal de una velocidad es de 45km/h.
Calcula la velocidad resultante si ésta forma un ángulo de
70° con la componente mencionada y halla la componente
vertical.
Nota: este problema requiere destreza matemática
131.57km/h y 123.63km/h
21)
Una lancha es jalada por dos fuerzas de 30N y 40N
22) Determina la magnitud y la dirección de la fuerza resultante
respectivamente. Si el ángulo entre las dos fuerzas es de
de la fuerza resultante del siguiente sistema de fuerzas:
F1=60N a 40°; F2=20N a 75°.
25, hallar la magnitud y la dirección de la fuerza resultante.
FR=77.2N, ΘR = 48.5 °
FR=68.4N y ΘR= 14.3 a partir de la fuerza de 30 N
Ing. Jaime Lomelí Cervantes
Página 9
Cuaderno de evidencias de Física II
Halla el vector resultante (magnitud y dirección) de los
siguientes vectores: V1= 125N, 1= 30° y V2 = 165N, 2=
140°.
VR = 169.53N y R = 96°
Preparatoria No. 22
23)
24)
25)
Un proyectil teledirigido se eleva sobre la superficie de la
26)
tierra a 45° a una velocidad constante de 540km/h. Halla la
altura sobre la superficie de la tierra a los 15
minutos.95.46Km
Ing. Jaime Lomelí Cervantes
Un automóvil Volvo recorre 80Km al oeste y luego 30km
hacia al suroeste. Determina la magnitud la dirección del
desplazamiento resultante del automóvil desde el punto de
partida.
DR =103.4km ΘR =11.83o (al sur del oeste) o ΘR=191.83 o
Un avión despega de la pista de aterrizaje a una velocidad
uniforme de 360km/h y con un ángulo de 30°. Calcula la
distancia horizontal que recorre en 120segundos a partir del
despegue. 10.39Km.
Página 10
Cuaderno de evidencias de Física II
27)
Un corredor de ultra distancia se desplaza 26km hacia el
norte y después corre 62km en dirección 30° al norte del
este. Calcula el desplazamiento resultante (magnitud y
dirección) del corredor.
DR = 78.3km y R = 46.71°
Preparatoria No. 22
28)
Un supersónico vuela al norte a razón de 100 m/s y es
empujado por el viento fuerte al oeste a razón de 50 m/s.
Calcula la velocidad resultante (magnitud y dirección) del
avión.
VR = 111.8 m/s y R = 63.43° (al norte del oeste) o R = 116.57°
Calcula la fuerza resultante de F1 =60N a 1 = 30° y F2=85N 30) Determina la fuerza resultante de F1 =56N a 1 =125° y F2
a 2 =140°.
=43N a 2 =220°
FR = 85.65N y R = 98.83°
FR = 67.56N y R =164.34°
29)
Ing. Jaime Lomelí Cervantes
Página 11
Cuaderno de evidencias de Física II
Preparatoria No. 22
Calcula la fuerza resultante de: F1=40N a 1=15°, F2=25N a 32) Calcula la fuerza resultante de:F1 =90N a 1 =85°, F2=20N
2=80°, F3=30N a 3=150° y F4=42N a 4=220°
a 2 =170° y F3 =40N a 3 =190°
FR = 27.5N, R = 123.4°
FR =100N, R =121°
31)
Determina la fuerza resultante de:F1=90N a 1=135°, F2
=80N a 2 =275° y F3 =48N a 3 =190°
FR = 106.76N ,R =193.2°
33)
Ing. Jaime Lomelí Cervantes
Calcula la fuerza resultante de:F1=2N a 1=12° y F2=3N,
2=300°
FR = 4.08, R =327.73°
34)
Página 12
Cuaderno de evidencias de Física II
35)
Calcula la fuerza resultante actuante sobre el objeto de la
figura.F1=800N, F2=1500N, F3=1000N y F4=1100N
FR=1996N Y θR=4.1°
Preparatoria No. 22
36)
Calcula la fuerza resultante actuante sobre el objeto de la
figura.F1=500N, F2=700N y F3=600N
FR= 1213.13 N Y θR=278.14°
°
Y
Y
F1
F2
20°
30°
15°
30°
X
F3
30°
X
25°
F3
F1
F2
F4
37)
Calcula la fuerza resultante actuante sobre el objeto de la
figura.F1=600N, F2=400N y F3=500N
FR=696N θR=154.1°
38)
Calcula la fuerza resultante actuante sobre el objeto de la
figura.F1=190N, F2=150N , F3=160N, F4=110N y F5=220N
FR=65N θR=331°
Y
Y
F1
F2
F3
F2
45°
20°
X
60°
60°
30°
F1
X
F4
F3
Ing. Jaime Lomelí Cervantes
F5
Página 13
Cuaderno de evidencias de Física II
Preparatoria No. 22
d) Vectoriales
AUTOEVALUACIÓN
RESUELVE LAS SIGUIENTES PREGUNTAS Y
PROBLEMAS DE SUMA DE VECTORES.
1. Cantidad física que solo tiene magnitud y queda
completamente definida mediante un número y una
cantidad.
a) Cantidad física
b) Cantidad escalar
c) Cantidad vectorial
d) Cantidad química
7. Son métodos usados en la suma de vectores:
a) Método gráfico (del polígono)
b) Método analítico (del paralelogramo y de las
componentes)
c) Método del círculo
d) Método del vértice
e) a y b son correctos
8. Figura correcta en la suma de vectores por el
método gráfico.
2. Cantidad física que tiene magnitud, dirección y
sentido.
a) Cantidad física
b) Cantidad escalar
c) Cantidad vectorial
d) Cantidad química
3.
a)
b)
c)
d)
e)
4.
a)
b)
c)
d)
e)
V1
A
V2
C
6. Vectores que actúan en un mismo plano se
llaman:
a) Concurrentes
b) Coplanares
c) Escalares
Ing. Jaime Lomelí Cervantes
VR
VR
V1
V2
D
V1
9. Figura incorrecta en la suma de vectores por el
método gráfico dadas las figuras:
V1
VR
A
V2
V3
V3
V1
V2
V3
VR
V1
E
V2
V1
V2
C
V1
B
V3
VR
VR
5. Es el resultado de la suma o de la resta existente
entre vectores, es decir dos o mas vectores se
pueden reemplazar por un solo vector con el mismo
efecto, llamado:
a) Vector resultante
b) Vector equilibrante
c) Cantidad escalar
d) Cantidad vectorial
V2
B
V1
V2
Son ejemplos de cantidades escalares:
Trabajo
Impulso
Fuerza
Rapidez
a y d lo son
Son ejemplos de cantidades vectoriales:
Trabajo
Impulso
Fuerza
Rapidez
b y c lo son
VR
VR
V2
V3
D
VR
10. Tiene la misma magnitud y dirección, pero
sentido contrario al vector resultante:
a) Vector resultante
b) Vector equilibrante
c) Cantidad escalar
d) Cantidad vectorial
11. Si dos vectores con la misma magnitud y el
mismo sentido se suman, el vector resultante es:
a) El triple de magnitud que los vectores originales y
con diferente dirección
Página 14
Cuaderno de evidencias de Física II
b) El doble de magnitud que los vectores originales y
con la misma dirección
c) El triple de magnitud que los vectores originales y
con la misma dirección
d) El doble de magnitud que los vectores originales y
con diferente dirección
12. Si dos vectores con la misma magnitud y sentido
contrario se suman, el vector resultante es:
a) El triple de magnitud que los vectores originales y
con diferente dirección
b) El doble de magnitud que los vectores originales y
con la misma dirección
c) Cero
d) Uno
13. Si una persona camina 60 metros al este y luego
40 metros al oeste, ¿cuál es su desplazamiento
resultante?
a) 20 metros al oeste
b) 20 metros al este
c) 100 metros al este
d) 100 metros al oeste
14. Si un auto avanza 55 Km al sur y luego 35 Km al
norte, ¿cuál es su desplazamiento resultante?
a) 20 Km al sur
b) 20 Km al norte
c) 90 Km al norte
d) 90 Km al sur
15. Si dos fuerzas de igual magnitud que se aplican
sobre un mismo punto y tienen sentidos contrarios,
¿cuál es la fuerza resultante?
a) El triple de magnitud que las fuerzas originales y
con diferente dirección
b) El doble de magnitud que los vectores originales y
con la misma dirección
c) Cero
d) Uno
16. Un hombre camina 16 km al este y luego 10 km al
norte. Calcula la magnitud y la dirección del
desplazamiento resultante.
a) DR= 18.87 km ØR= 132º al norte del este
b) DR= 18.87 km ØR= 143º al norte del este
c) DR= 18.87 km ØR= 243º al norte del este
Ing. Jaime Lomelí Cervantes
Preparatoria No. 22
d) DR= 18.87 km ØR= 32º al norte del este
e) DR= 18.87 km ØR= 43º al norte del este
17. Un hombre camina 9 km hacia el este y luego 6
km hacia el sur. Calcula la magnitud y la dirección del
desplazamiento resultante.
a) DR= 108.2 km ØR= 33.7º al sur del este
b) DR= 10.82 km ØR= 233.7º al sur del este
c) DR= 10.82 km ØR= 33.7º al sur del este
d) DR= 10.82 km ØR= 333.7º al sur del este
e) DR= 82
km ØR= 33.7º al sur del este
18. Dos fuerzas de 60N y 80N se aplican sobre un
cuerpo formando un ángulo de 35º entre ellas.
Encuentra la magnitud de la fuerza resultante y su
dirección respecto a la fuerza más pequeña.
a) FR= 653.65N ØR= 20.5º
b) FR= 133.13N ØR= 28.5º
c) FR= 333.65N ØR= 128.5º
d) FR= 133.65N ØR= 20º
e) FR= 133.65N ØR= 28.5º
19. Para
FR 
qué
 Fx   Fy
2
2
se
utiliza
la
ecuación
en la suma de vectores por el
método analítico
a) Para calcular la dirección del vector resultante
b) Para calcular la ubicación del vector resultante en
uno de los cuatro cuadrantes del sistema
cartesiano
c) Para calcular la magnitud del vector resultante
d) Para calcular el ángulo resultante
20. Para qué se utiliza el signo de ΣFx y ΣFy en la
suma de vectores, por el método analítico.
a) Para calcular la magnitud del vector resultante
b) Para calcular la dirección del vector resultante
c) Para calcular la ubicación del vector resultante en
uno de los cuatro cuadrantes del sistema
cartesiano
d) Para calcular el ángulo resultante
21. Para qué se utiliza la ecuación
Tan 
 Fy en el
 Fx
método analítico.
a) Para calcular la magnitud del vector resultante
b) Para calcular la dirección del vector resultante
Página 15
Cuaderno de evidencias de Física II
c) Para calcular la ubicación del vector resultante en
uno de los cuatro cuadrantes del sistema
cartesiano
d) Para calcular el ángulo con respecto al eje x
e) Para calcular el ángulo resultante
22. Encuentra la magnitud y dirección del vector
resultante de los siguientes vectores:
V1 = 45 N a 25º y V2 = 60N a 70º
a) VR= 97.17N ØR= 61.2º
b) VR= 97.17N ØR= 51º
c) VR= 107.17N ØR= 61.2º
d) VR= 97.907N ØR= 151º
e) VR= 97.408N ØR= 16.2º
23. Dos fuerzas de 50N y 94N, respectivamente se
emplean para arrastrar un bote por el agua. Si el
ángulo entre ellas es de 40º, Hallar la magnitud de la
fuerza resultante y su dirección con respecto a la
fuerza mas pequeña.
a) FR= 136.15N ØR= 26.3º
b) FR= 163.15N ØR= 14.53º
c) FR= 123.15N ØR= 62.3º
d) FR= 159.15N ØR= 26.9º
Ing. Jaime Lomelí Cervantes
Preparatoria No. 22
e) FR= 163.15N ØR= 172.53º
24. Hallar la magnitud y la dirección del vector
resultante de los siguientes vectores: V1= 125N a 30º
y V2= 165N a 140º
a) VR=135.28N ØR=90o
b) VR=169.5N ØR= 96.1º
c) VR=153.28N ØR=96o
d) VR=133.28N ØR=95o
e) VR=135.25N ØR=94o
25. Encuentra la magnitud y la dirección de la fuerza
resultante del siguiente sistema de fuerzas: F1= 20N a
30º F2= 4N a 0º F3= 3N a 90º F4= 30N a 116º F5=
15N a 200º F6= 14N a 320º
a) FR= 26.27N ØR= 86º
b) FR= 26.27N ØR= 79.5º
c) FR= 4.9N
ØR= 347º
d) FR= 4.9N
ØR= 35º
e) FR=97.17N ØR=51º
Página 16
Cuaderno de evidencias de Física II
Preparatoria No. 22
VECTORES
SUS CARACTERÍSTICAS
SON:
______________________
______________________
SU DEFINICIÓN ES:
______________________
______________________
LOS MÉTODOS DE
SOLUCIÓN SON:
GRÁFICOS
1. ________________________
2. ________________________
3. ________________________
EL MATERIAL
UTILIZADO ES:
1. ________________________
2. ________________________
3. ________________________
Ing. Jaime Lomelí Cervantes
ANALÍTICOS
1. ________________________
2. ________________________
3. ________________________
LAS HERRAMIENTAS
MATEMÁTICAS SON:
1. ________________________
2. ________________________
3. ________________________
Página 17
Cuaderno de evidencias de Física II
Preparatoria No. 22
APÉNDICE
ELEMENTOS DE UN VECTOR:
A) Punto de aplicación.- Está dado por el
origen del vector.
B) Vectores concurrentes
Son aquellos vectores cuyas líneas de acción, se
cortan en un solo punto; el punto de cruce
constituye el punto de aplicación de los vectores.
B) Intensidad, módulo o magnitud.- Es el
valor del vector, y generalmente, está dado
en escala. ej. 5 unidades de longitud
equivale a 5 N (si se tratase de fuerza).
C) Sentido.- Es la orientación del vector.
D) Dirección.- Está dada por la línea de
acción del vector o por todas las líneas
rectas paralelas a él.
C) Vectores coplanares
Son aquellos vectores que están contenidos en un
mismo plano o dos ejes x y y.
C) Vectores no coplanares
ALGUNOS TIPOS DE VECTORES:
Son aquellos vectores que están contenidos en
diferente plano como x, y y z.
A) Vectores colineales
Son aquellos vectores que están contenidos en
una misma línea de acción o dirección. Un vector
colineal es positivo si su sentido es hacia arriba o
hacia la derecha y negativo si su sentido es hacia
abajo o a la izquierda, por convención.
Ing. Jaime Lomelí Cervantes
Página 18
Cuaderno de evidencias de Física II
D) Vectores iguales
Son aquellos vectores que tienen la misma
intensidad, dirección y sentido.
Preparatoria No. 22
Los vectores no se modifican si se trasladan
paralelamente a sí mismos.
G) Adición de vectores
Sumar dos o más vectores, es representarlos por uno
sólo llamado resultante. Este vector resultante produce
los mismos efectos que todos juntos. Hay que tener en
cuenta que la suma vectorial no es lo mismo que la suma
aritmética.
Páginas web que puede consultar el alumno y el maestro:
http://www.walter-fendt.de/ph14s/
E) Vector opuesto (-A)
http://www.walter-fendt.de/ph14s/resultant_s.htm
Se llama vector opuesto (-A) de un vector A
cuando tienen el mismo módulo, la misma
dirección, pero sentido contrario.
http://www.educaplus.org/movi/1_4sumavector.html
Rosa de los vientos
90°
0°
180°
F) Propiedades de los vectores
Transmisibilidad del punto de aplicación.
El efecto externo de un vector deslizante no se modifica
si es trasladado en su misma dirección. Por ejemplo es lo
mismo jalar o empujar horizontalmente un cuerpo.
Ing. Jaime Lomelí Cervantes
270°
Página 19